5: C5) Conservation of Momentum
- Page ID
- 63153
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- 5.1: Conservation of Linear Momentum
- The law of conservation of momentum says that the momentum of a closed system is constant in time (conserved). A closed (or isolated) system is defined to be one for which the mass remains constant, and the net external force is zero. The total momentum of a system is conserved only when the system is closed.
In this chapter we are going to combine what we've done in Chapter 2 and Chapter 3, and introduce the law of conservation of momentum, which is the first real "rule" of nature that we are going to study in this book. In Chapter 2 we used this law in the form "interactions transfer momentum". That is the core concept, but it turns out that really implementing this is challenging without some mathematical tools - primarily that of vectors. Now that we have a better understanding of (and some practice doing) vector analysis, we are ready to state the full law of conservation of momentum: the momentum of an isolated system does not change in time. This is a seemingly simple statement, but it turns out to be extraordinarily powerful, because you can use it to make predictions about the systems you are studying - the final velocity of an object in a collision, for instance.
Of course, to make quantitative predictions, we need cast this law into mathematics, which is the following:
\[\Delta \vec{p}=0 \Leftrightarrow \vec{p}_f-\vec{p}_i=0 \Leftrightarrow \vec{p}_f=\vec{p}_i \]
(You should convince yourself that all three of those statements say exactly the same thing, using the definition of the delta and basic algebra!)
We should take note that this is a vector equation, which means there are actually two parts to it: \(\Delta p_x=0\) and \(\Delta p_y=0\). These two equations are independent, in the sense that they always both true at the same time, but aren't directly related.
Let's also just briefly note how we should understand this mathematical statement in conjunction with our old "interactions transfer momentum" concept. If a system is isolated, there are no interactions between the system and the outside world, so there is no momentum transfer into or out of the system. That's exactly the same information contained in the equation above, since that says the change in momentum of an isolated system is zero.
Let's try some examples. Say you have a hockey puck (mass 0.5 kg) sliding on ice at a speed of 10 m/s, and it collides head on into another puck moving at 14 m/s. After the collision, the second puck moves away at 6 m/s, and we can use our laws to determine the final speed of the first. The equation says "final equals initial", so let's try to calculate the initial. The first puck has a momentum of 5 kg m/s, the second has 7 kg m/s - but it's moving the opposite direction, so the initial momentum in the x-direction is \(p_{i,x}=5 \text{ kg m/s} - 7 \text{ kg m/s} = -2 \text{ kg m/s}\). We can also try to calculate the final momentum - the second puck has 3 kg m/s, in the positive direction, but we don't know the final speed of the first. However, using the equation above we can write
\[-2 \text{ kg m/s} = (0.5 \text{ kg})v_{1,f}+3 \text{ kg m/s}.\]
This equation can be solved for the unknown variable to get \(v_{1,f}=-10 \text{ m/s}\), which is negative because apparently the first puck bounces off the second and moves backward after the collision.
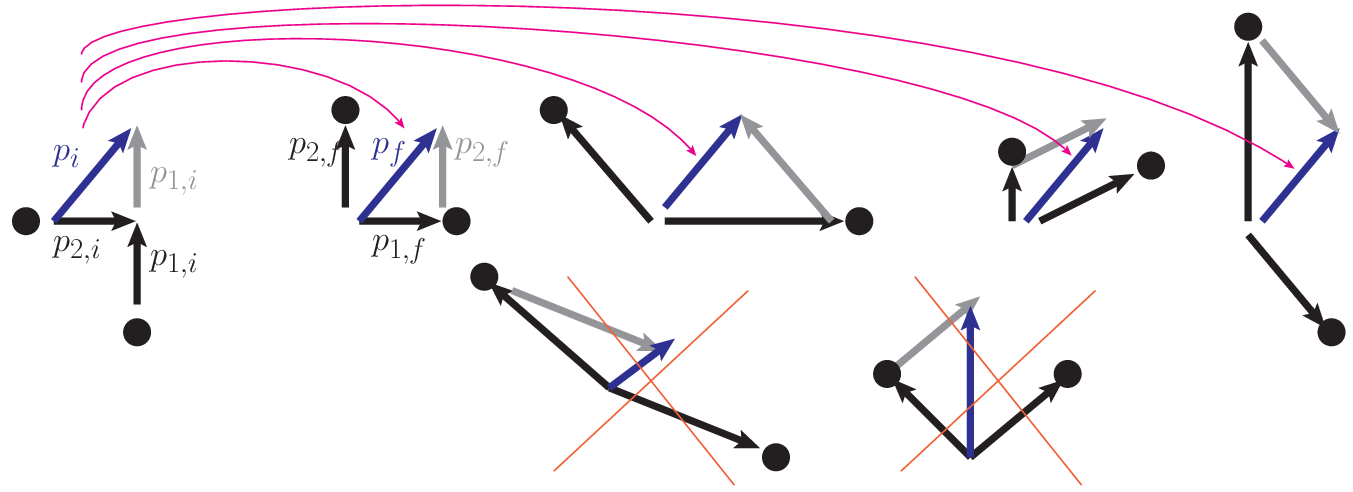
That example was pretty simple, since the collision only took place in a single direction (we chose x). However, our conservation of momentum law tells us that the vector (magnitude and direction) of the momentum must remain unchanged during a collision. The figure below illustrates that for the collision of two objects of similar masses (note the grey arrows are just helping us to make sure we add the vectors head to tail). The final momentum must be equal to the initial, and even though some of the collisions below look totally reasonable, they are prohibited by the law of conservation of momentum.