7: C7) Conservation of Angular Momentum II

Last updated
Save as PDF

Page ID: 63161

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

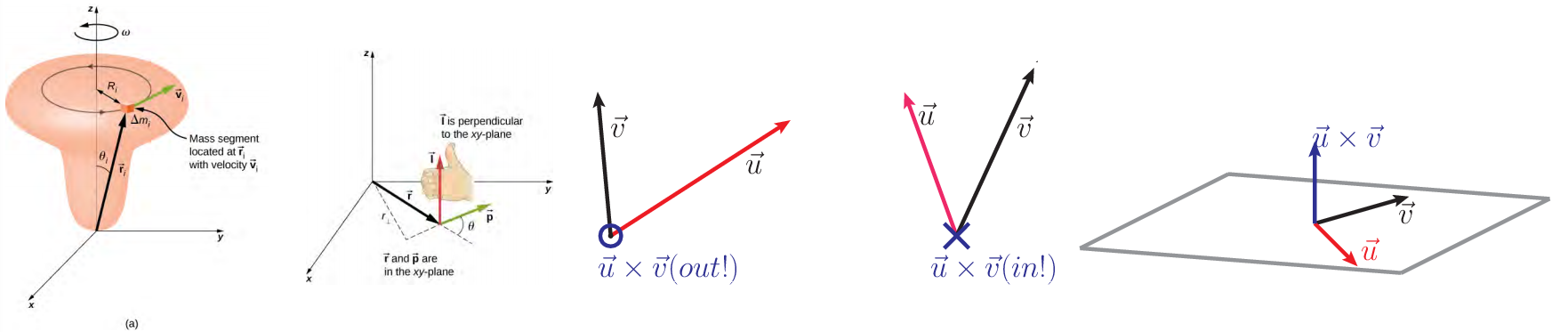
In the previous chapter, we dealt with objects having real size for the first time, and we learned how to calculate the angular momentum for extended objects as \(\vec{L}=I\vec{\omega}\). In this chapter, we have to acknowledge that if extended objects can have angular momenta, singular points can also! This sounds very counter-intutiive, so let's first make sure we understand why that must be - essentially, objects are made up of points, and we believe angular momentum should be additive (two objects with angular momentum \(L_1\) and \(L_2\) have total angular momentum \(L_1+L_2\)...sounds like something we want, right?). If that's true, then when you think about an extended object as a collection of points, each of those points should have individual angular momenta \(L_i\) so that we can add them all to get the total \(L=\sum_i L_i\).

Of course, those individual points themselves are not spinning, they are moving around the axis of the object (see the leftmost figure below). But how do we determine the angular momenta of these individual points? The answer is to use a cross-product:

\[\vec{L}=\vec{r} \times \vec{p}.\]

In this formula, the \(\vec{r}\) is the position of the point and \(\vec{p}\) is the momentum. We will go into this equation in some detail in the rest of the chapter, but the important thing to notice now is that it is a vector, so it has magnitude and direction. The magnitude can be found with the formula

\[|L|=|r||p|\sin\phi,\]

where \(\phi\) is the angle between \(\vec{r}\) and \(\vec{p}\). The direction of any cross product \(\vec{u}\times \vec{v}\) can be found with the right hand rule. The right hand rule (see second figure to the right) says:

Point (the fingers on your right hand!) in the direction of the first vector in \(\vec{u}\times \vec{v}\).
Curl your fingers into the second vector in \(\vec{u}\times \vec{v}\) (you may need to flip you hand around...)
Your thumb is now pointing in the direction of \(\vec{u}\times \vec{v}\).

"This" right hand rule is actually related to the "first" right hand rule we learned in the last chapter for the direction of \(\vec{L}=I\vec{\omega}\), but the one presented here works for any cross product, whereas the other one is just for the angular momentum of an object. The figure below (three images on the right) illustrates a few examples of these directions - check that you can get the right answers!

(images from Open Stax!)