8.1: Time Is Not Absolute
- Page ID
- 958
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When Einstein first began to develop the theory of relativity, around 1905, the only real-world observations he could draw on were ambiguous and indirect. Today, the evidence is part of everyday life. For example, every time you use a GPS receiver, a, you're using Einstein's theory of relativity. Somewhere between 1905 and today, technology became good enough to allow conceptually simple experiments that students in the early 20th century could only discuss in terms like “Imagine that we could...”

A good jumping-on point is 1971. In that year, J.C. Hafele and R.E. Keating brought atomic clocks aboard commercial airliners, b, and went around the world, once from east to west and once from west to east. Hafele and Keating observed that there was a discrepancy between the times measured by the traveling clocks and the times measured by similar clocks that stayed home at the U.S. Naval Observatory in Washington. The east-going clock lost time, ending up off by \(-59\pm10\) nanoseconds, while the west-going one gained \(273\pm7\) ns.

b / The clock took up two seats, and two tickets were bought for it under the name of “Mr. Clock.”
7.1.1 The correspondence principle
This establishes that time doesn't work the way Newton believed it did when he wrote that “Absolute, true, and mathematical time, of itself, and from its own nature flows equably without regard to anything external...” We are used to thinking of time as absolute and universal, so it is disturbing to find that it can flow at a different rate for observers in different frames of reference. Nevertheless, the effects that Hafele and Keating observed were small. This makes sense: Newton's laws have already been thoroughly tested by experiments under a wide variety of conditions, so a new theory like relativity must agree with Newton's to a good approximation, within the Newtonian theory's realm of applicability. This requirement of backward-compatibility is known as the correspondence principle.
7.1.2 Causality
It's also reassuring that the effects on time were small compared to the three-day lengths of the plane trips. There was therefore no opportunity for paradoxical scenarios such as one in which the east-going experimenter arrived back in Washington before he left and then convinced himself not to take the trip. A theory that maintains this kind of orderly relationship between cause and effect is said to satisfy causality.
Causality is like a water-hungry front-yard lawn in Los Angeles: we know we want it, but it's not easy to explain why. Even in plain old Newtonian physics, there is no clear distinction between past and future. In figure c, number 18 throws the football to number 25, and the ball obeys Newton's laws of motion. If we took a video of the pass and played it backward, we would see the ball flying from 25 to 18, and Newton's laws would still be satisfied. Nevertheless, we have a strong psychological impression that there is a forward arrow of time.
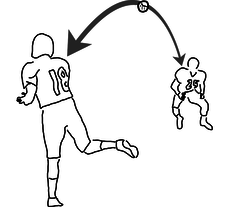
c / Newton's laws do not distinguish past from future. The football could travel in either direction while obeying Newton's laws.
I can remember what the stock market did last year, but I can't remember what it will do next year. Joan of Arc's military victories against England caused the English to burn her at the stake; it's hard to accept that Newton's laws provide an equally good description of a process in which her execution in 1431 caused her to win a battle in 1429. There is no consensus at this point among physicists on the origin and significance of time's arrow, and for our present purposes we don't need to solve this mystery. Instead, we merely note the empirical fact that, regardless of what causality really means and where it really comes from, its behavior is consistent. Specifically, experiments show that if an observer in a certain frame of reference observes that event A causes event B, then observers in other frames agree that A causes B, not the other way around. This is merely a generalization about a large body of experimental results, not a logically necessary assumption. If Keating had gone around the world and arrived back in Washington before he left, it would have disproved this statement about causality.
7.1.3 Time distortion arising from motion and gravity
Hafele and Keating were testing specific quantitative predictions of relativity, and they verified them to within their experiment's error bars. Let's work backward instead, and inspect the empirical results for clues as to how time works.
The two traveling clocks experienced effects in opposite directions, and this suggests that the rate at which time flows depends on the motion of the observer. The east-going clock was moving in the same direction as the earth's rotation, so its velocity relative to the earth's center was greater than that of the clock that remained in Washington, while the west-going clock's velocity was correspondingly reduced. The fact that the east-going clock fell behind, and the west-going one got ahead, shows that the effect of motion is to make time go more slowly. This effect of motion on time was predicted by Einstein in his original 1905 paper on relativity, written when he was 26.
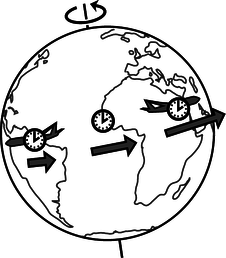
If this had been the only effect in the Hafele-Keating experiment, then we would have expected to see effects on the two flying clocks that were equal in size. Making up some simple numbers to keep the arithmetic transparent, suppose that the earth rotates from west to east at 1000 km/hr, and that the planes fly at 300 km/hr. Then the speed of the clock on the ground is 1000 km/hr, the speed of the clock on the east-going plane is 1300 km/hr, and that of the west-going clock 700 km/hr. Since the speeds of 700, 1000, and 1300 km/hr have equal spacing on either side of 1000, we would expect the discrepancies of the moving clocks relative to the one in the lab to be equal in size but opposite in sign.

e / A graph showing the time difference between two atomic clocks. One clock was kept at Mitaka Observatory, at 58 m above sea level. The other was moved back and forth to a second observatory, Norikura Corona Station, at the peak of the Norikura volcano, 2876 m above sea level. The plateaus on the graph are data from the periods when the clocks were compared side by side at Mitaka. The difference between one plateau and the next shows a gravitational effect on the rate of flow of time, accumulated during the period when the mobile clock was at the top of Norikura. Cf. problem 25, p. 443.
In fact, the two effects are unequal in size: \(-59\) ns and 273 ns. This implies that there is a second effect involved, simply due to the planes' being up in the air. This was verified more directly in a 1978 experiment by Iijima and Fujiwara, figure e, in which identical atomic clocks were kept at rest at the top and bottom of a mountain near Tokyo. This experiment, unlike the Hafele-Keating one, isolates one effect on time, the gravitational one: time's rate of flow increases with height in a gravitational field. Einstein didn't figure out how to incorporate gravity into relativity until 1915, after much frustration and many false starts. The simpler version of the theory without gravity is known as special relativity, the full version as general relativity. We'll restrict ourselves to special relativity until section 7.4, and that means that what we want to focus on right now is the distortion of time due to motion, not gravity.
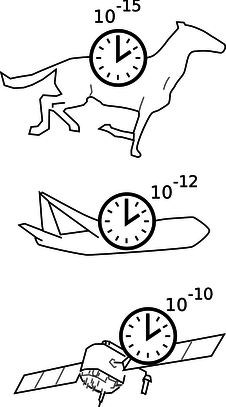
We can now see in more detail how to apply the correspondence principle. The behavior of the three clocks in the Hafele-Keating experiment shows that the amount of time distortion increases as the speed of the clock's motion increases. Newton lived in an era when the fastest mode of transportation was a galloping horse, and the best pendulum clocks would accumulate errors of perhaps a minute over the course of several days. A horse is much slower than a jet plane, so the distortion of time would have had a relative size of only \(\sim10^{-15}\) --- much smaller than the clocks were capable of detecting. At the speed of a passenger jet, the effect is about \(10^{-12}\), and state-of-the-art atomic clocks in 1971 were capable of measuring that. A GPS satellite travels much faster than a jet airplane, and the effect on the satellite turns out to be \(\sim10^{-10}\). The general idea here is that all physical laws are approximations, and approximations aren't simply right or wrong in different situations. Approximations are better or worse in different situations, and the question is whether a particular approximation is good enough in a given situation to serve a particular purpose. The faster the motion, the worse the Newtonian approximation of absolute time. Whether the approximation is good enough depends on what you're trying to accomplish. The correspondence principle says that the approximation must have been good enough to explain all the experiments done in the centuries before Einstein came up with relativity.
By the way, don't get an inflated idea of the importance of the Hafele-Keating experiment. Special relativity had already been confirmed by a vast and varied body of experiments decades before 1971. The only reason I'm giving such a prominent role to this experiment, which was actually more important as a test of general relativity, is that it is conceptually very direct.
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


