10.2: Elements of an Elliptic Orbit
( \newcommand{\kernel}{\mathrm{null}\,}\)
Six numbers are necessary and sufficient to describe an elliptic orbit in three dimensions. These include the four (a, e, ω and T) that we described in section 9.9 for the two dimensional case. Two additional angles, which will be given the symbols i and Ω, will be needed to complete the description of the orbit in 3-space.
The six elements of an elliptic orbit, then, are as follows.
a the semi major axis, usually expressed in astronomical units (\text{AU}).
e the eccentricity
i the inclination
Ω the longitude of the ascending node
ω the argument of perihelion
T the time of perihelion passage
The three angles, i, Ω and ω must always be referred to the equinox and equator of a stated epoch. For example, at present they are usually referred to the mean equinox and equator of \text{J2000.0}. The meanings of the three angles are explained in figure \text{X.1} and the following paragraphs.
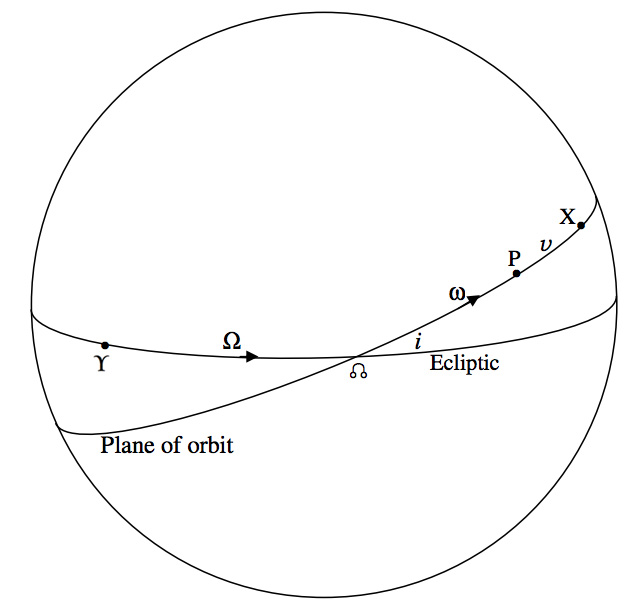
\text{FIGURE X.1}
In figure \text{X.1} I have drawn a celestial sphere centred on the Sun. The two great circles are intended to represent the plane of Earth’s orbit (i.e. the ecliptic) and the plane of a planet’s orbit – (i.e. not the orbit itself, but its projection on to the celestial sphere.) The point \text{P} is the projection of the perihelion point of the orbit on to the celestial sphere, and the point \text{X} is the projection of the planet on to the celestial sphere at some time. The two points where the plane of the ecliptic and the plane of the planet’s orbit intersect are called the nodes, and the point marked is the ascending node. The descending node, , not shown in the figure, is on the far side of the sphere. The symbol is the First point of Aries (now in the constellation Pisces), where the ecliptic crosses the equator. As seen from the Sun, Earth is at on \Upsilon or near September 22. (For the benefit of personal computer users, I found the symbols , and \Upsilon in Bookshelf Symbol 3.) \multimap
The inclination i is the angle between the plane of the object’s orbit and the plane of the ecliptic (i.e. of Earth’s orbit). It lies in the range o o 0 ≤ i < 180 . An inclination greater than 90o implies that the orbit is retrograde – i.e. that it is moving around the Sun in a direction opposite to that of Earth’s motion.
The angle Ω, measured eastward from \Upsilon to mulitmapinv, is the ecliptic longitude of the ascending node. (The word “ecliptic” is usually omitted as understood.) It goes from 0^\circ to 360^\circ.


