16.1: Introduction
( \newcommand{\kernel}{\mathrm{null}\,}\)
We are going to consider the following problem. Two masses, M1 and M2 are revolving around their mutual centre of mass C in circular orbits, at a constant distance a apart.

FIGURE IV.4
The orbital period is given by
P^2 = \frac{4π^2 a^3}{G (M_1 + M_2)} \label{16.1.1} \tag{16.1.1}
and the angular orbital speed is given by
ω^2 = \frac{G(M_1 M_2)}{a^3} . \label{16.1.2} \tag{16.1.2}
I establish the following notation.
Mass ratio: \frac{M_1}{M_2} = q . \label{16.1.3} \tag{16.1.3}
Mass fraction: \frac{M_1}{M_1 + M_2} = µ . \label{16.1.4} \tag{16.1.4}
They are related by q = \frac{µ}{1 - µ} \label{16.1.5} \tag{16.1.5}
and µ = \frac{q}{1 + q} . \label{16.1.6} \tag{16.1.6}
We note the following distances:
\text{M}_1 \text{C} = (1 - µ) a , \quad \text{M}_2 \text{C} = µ a . \label{16.1.7} \tag{16.1.7}
We ask ourselves the following question: Are there any points on the line passing through the two masses where a third body of negligible mass could orbit around \text{C} with the same period as the other two masses; i.e. it would remain on the line joining the two main masses?
In fact there are three such points, and they are known as the collinear lagrangian points. (The collinear points were discussed by Euler before Lagrange, but Lagrange took the problem further and discovered an additional two points not collinear with the masses, and the five points today are generally all known as the lagrangian points. We shall discuss the additional points in Section 16.2.) I have marked the three points in figure \text{XVI.4} with the letters \text{L}_1, \text{L}_2 and \text{L}_3.
There are evidently 3! = 6 ways in which I could choose the subscripts. Often today, the inner lagrangian point is labelled \text{L}_1 and the outer points are labelled \text{L}_2 and \text{L}_3. This seems to me to lack logic, and I choose to label the inner point \text{L}_3, and the outer points associated with M_1 and M_2 are then \text{L}_1 and \text{L}_2 respectively. Incidentally, I am not making any assumption about which of the two main bodies is the more massive.
Let us deal first with \text{L}_1. Let us suppose that the distance from \text{C} to \text{L}_1 is xa.
A particle of mass m at \text{L}_1 is subject (in a co-rotating reference frame) to three forces, namely the gravitational attractions from the two main bodies, and the centrifugal force acting away from \text{C}. If this body is to be in equilibrium, we must have
\frac{GM_1 m}{[(x - 1 + µ)a]^2} + \frac{GM_2 m}{[(x + µ) a]^2} = mxa ω^2 . \label{16.1.8} \tag{16.1.8}
On making use of Equations 16.1.2 and 16.1.4, we find that this Equation becomes
\frac{µ}{(x -1 + µ)^2} + \frac{1- µ}{(x + µ)^2} = x . \label{16.1.9} \tag{16.1.9}
After manipulation, this becomes
a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + x^5 = 0 , \label{16.1.10} \tag{16.1.10}
where a_0 = -1 + 3 µ - 3µ^2 , \label{16.1.11} \tag{16.1.11}
a_1 = 2 - 4 µ + µ^2 - 2 µ^3 + µ^4 , \label{16.1.12} \tag{16.1.12}
a_2 = -1 + 2µ - 6µ^2 + 4µ^3 , \label{16.1.13} \tag{16.1.13}
a_3 = 1 - 6µ + 6µ^2 \label{16.1.14} \tag{16.1.14}
and a_4 = -2 + 4µ . \label{16.1.15} \tag{16.1.15}
Although Equation \ref{16.1.10} is a quintic Equation, it has just one real root for positive µ.
The positions of \text{L}_2 and \text{L}_3 can be found by exactly similar arguments – you just have to take care with the directions and distances of the two gravitational forces.
For \text{L}_2, the coefficients are the same as for \text{L}_1, except
a_1 = -2 + 4µ + µ^2 - 2µ^3 + µ^4 , \label{16.1.16} \tag{16.1.6}
a_2 = -1 - 2µ + 6µ^2 - 4µ^3 \label{16.1.17} \tag{16.1.17}
and a_4 = 2 - 4 µ . \label{16.1.18} \tag{16.1.18}
For \text{L}_3 the coefficients are
\begin{align} a_0 &= 1 - 3µ + 3µ^2 - 2µ^3 , \label{16.1.19} \\[5pt] a_1 &= 2 - 4µ + 5µ^2 - 2µ^3 + µ^4 , \label{16.1.20} \\[5pt] a_2 &= 1 - 4µ + 6µ^2 - 4µ^3 , \label{16.1.21} \\[5pt] a_3 &= 1 - 6µ + 6µ^2 \label{16.1.22} \\[5pt] a_4 &= 2 - 4µ . \label{16.1.23} \end{align}
(Reminder: When computing any of these polynomials, write them in terms of nested parentheses. See Chapter 1, Section 1.5.)
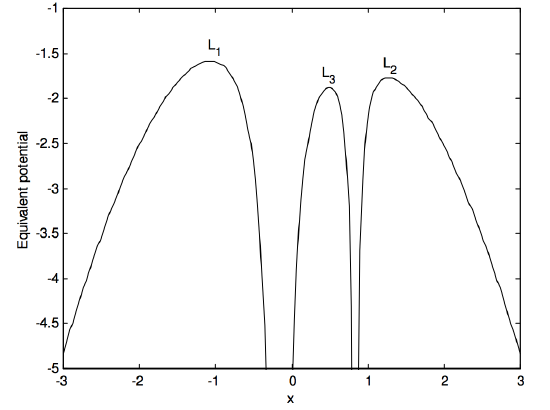
It is also of interest to see the equivalent potential (gravitational plus centrifugal). The expression for gravitational potential energy is, as usual, −GMm/r, where r is the distance from the mass M. The expression for the centrifugal potential energy is -\frac{1}{2} m ω^2 r^2, where r is the distance from the centre of mass. The negative of the derivative of this expression is mω^2 r which is the usual expression for the centrifugal force. When we apply these principles to the system of two masses under consideration, we obtain the following expression for the equivalent potential (which, in this section, I’ll just call V rather than V^\prime).
V = - \frac{GM_1}{|x + 1 - µ| a} - \frac{GM_2}{|x - µ| a} - \frac{1}{2}x^2 a^2 ω^2 . \label{16.1.24} \tag{16.1.24}
On making use of Equations \ref{16.1.2} and \ref{16.1.4}, we find that this Equation becomes
W = - \frac{µ}{|x + 1 - µ|} - \frac{1 - µ}{|x - µ|} - \frac{x^2}{2}, \label{16.1.25} \tag{16.1.25}
where W = V \div \left( \frac{G(M_1 + M_2)}{a} \right) . \label{16.1.26} \tag{16.1.26}
Setting the derivatives of this expression to zero gives, of course, the positions of the lagrangian points, for these are equilibrium points where the derivative of the potential is zero. Figure \text{XVI.5} shows the potential for a mass ratio q = 5. Note that, in the line joining the two masses, the equivalent potential at the lagrangian points is a maximum, and therefore these points, while equilibrium points, are unstable. We shall see in Section 16.6 that the points are actually saddle points. While several spacecraft are in orbit or are planned to be in orbit around the collinear lagrangian points (e.g. \text{SOHO} at the interior lagrangian point, and \text{MAP} at \text{L}_2), continued small expenditure of fuel is presumably needed to keep them there.
It will be of interest to see how the positions of the lagrangian points vary with mass fraction. Indeed mass can be transferred from one member of a binary star system to the other during the evolution of a binary star system. We shall discuss a little later how this can happen. For the time being, without worrying about the exact mechanism, we’ll just vary the mass fraction and see how the positions of the lagrangian points vary as we do so. However, if mass is transferred from one member of a binary star system to the other,
\text{FIGURE XVI.5}
and if there are no external torques on the system, the angular momentum L of the system will be conserved, and, to ensure this, the separation a of the two stars changes with mass fraction.
Show that, for a given orbital angular momentum L of the system, the separation a of the components varies with mass fraction according to
a = \frac{L^2}{GM^3 µ^2 (1-µ)^2}. \label{16.1.27} \tag{16.1.27}
Solution
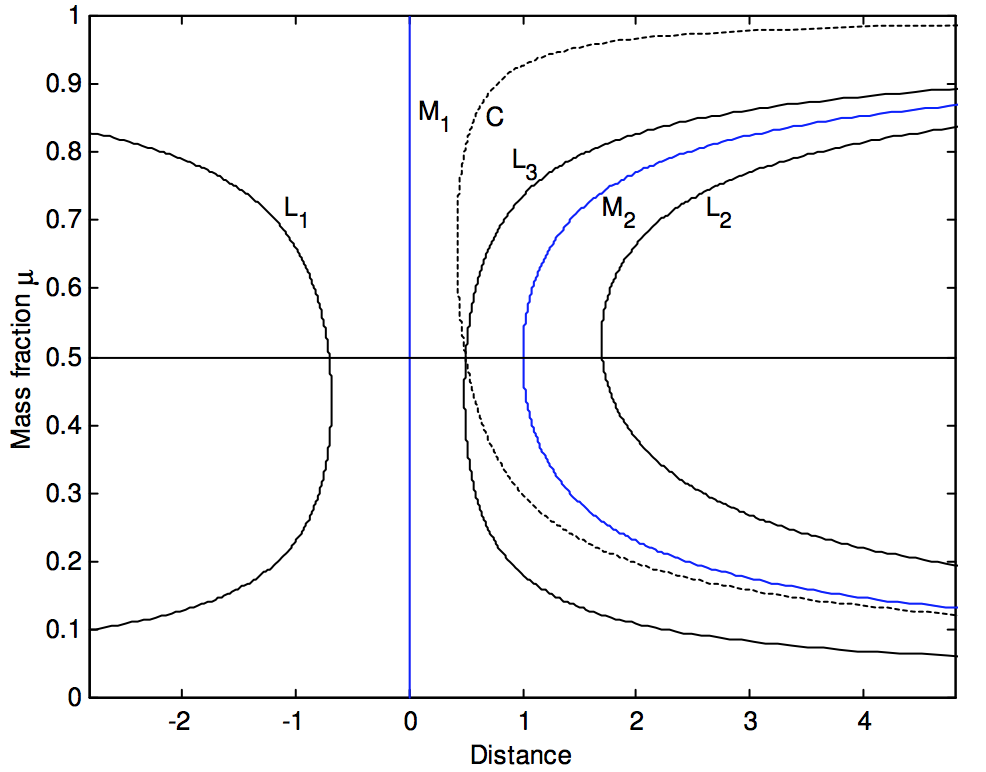
Here M = M_1 + M_2 is the total mass of the system. In figure \text{XVI.6} I have used this Equation, plus Equations \ref{16.1.10} and \ref{16.1.7}, to compute the distances of \text{M}_2, \text{C}, and the three lagrangian points from \text{M}_1 as a function of mass fraction. The unit of distance in figure \text{XVI.6} is 16 L^2 /(GM^3), which is the separation of the two masses when the two masses are equal. Each of these distances has a minimum value for a particular mass fraction. These minimum distances, and the mass fractions for which they occur, are as follows:
\begin{array}{c c c} & \text{Least value} & \text{Mass fraction} \\ \text{M}_1 \text{C} & 0.421875^* & 0.66666 \dot{6} \\ \text{M}_1 \text{L}_2 & 1.690392 & 0.524579 \\ \text{M}_1 \text{M}_2 & 1.000000 & 0.500000 \\ \text{M}_1 \text{L}_3 & 0.489038 & 0.446273 \\ \text{M}_1 \text{L}_1 & 0.677756 & 0.436062 \\ \end{array}
^* 0.421875 = 27/64 \ \text{exactly}
\text{FIGURE XVI.6}
How can mass transfer actually occur in a binary star system? Well, stars are not points – they are large spherical bodies. When the hydrogen is exhausted in the core by thermonuclear reactions, a star expands hugely (“leaves the main sequence”) and when it expands so much that the outer layers of its atmosphere reach the inner lagrangian point, matter from the large star spills over into the other star. The more massive of the two stars in a binary system generally evolves faster; it is the first to leave the main sequence and to expand so that its atmosphere reaches the inner lagrangian points. One can imagine the more massive star gradually filling up its potential well of figure \text{XVI.5}, until it overflows and drips over the potential hill of the inner point, and then falls into the potential well of its companion.
One way of interpreting figure \text{XVI.6} is to imagine that \text{M}_1 starts with a large mass fraction close to 1, and therefore near the top of figure \text{XVI.6}. Now imagine that this star loses mass to its companion, so that the mass fraction decreases. We start moving down the \text{M}_1 line of figure \text{XVI.6}. We see the inner point \text{L}_3 coming closer and closer. If the surface of the star meets \text{L}_3 while \text{L}_3 is still approaching (i.e. if the mass fraction is still greater than 0.446273), then further mass transfer will make \text{L}_3 approach ever faster, and mass transfer will therefore be rapid. When the mass fraction is less than 0.5, the star that was originally the more massive star is by now less massive than its companion. When the mass fraction has been reduced below 0.446273, further mass transfer will push \text{L}_3 away, and therefore further mass transfer will be slow.
In the calculations of Example \PageIndex{1}, I assumed that the stars can be treated gravitationally as if they are point sources – and so they can be, however large they are, as long as they are spherically symmetric. By the onset of mass transfer, the mass-losing star is quite distorted and is far from spherical. However, this distortion affects mostly the outer atmosphere of the star, and, provided that the greater bulk of the star is contained within a roughly spherically-symmetric volume, the point source approximation should continue to be good. The other assumption I made was that orbital angular momentum is conserved. There are two reasons why this might not be so – but for both of them there is likely to be very little loss of orbital angular momentum. One possibility is that mass might be lost from the system – through one or other or both of the external collinear lagrangian points. However, figure \text{XVI.5} shows that the potentials of these points are appreciably higher than the internal point; therefore mass transfer takes place well before mass loss. Another reason why orbital angular momentum might be conserved is as follows. When matter from the mass-losing star is transferred through the inner point to the mass-gaining star, or flows over the inner potential hill, it does not move in a straight line directly towards the second star. This entire analysis has been referred to a corotating reference frame, and when matter moves from \text{M}_1 towards \text{M}_2, it is subject to a Coriolis force (see section 4.9 of Classical Mechanics), which sends it around \text{M}_2 in an accretion disc. During this process the total angular momentum of the system is conserved (provided no mass is lost from the system) but this must now be shared between the orbital angular momentum of the two stars and the angular momentum of the accretion disc. However, as long as the latter is a relatively small contribution to the total angular momentum, conservation of orbital angular momentum remains a realistic approximation.


