9.2: Kepler's Second Law from Conservation of Angular Momentum
- Page ID
- 6842
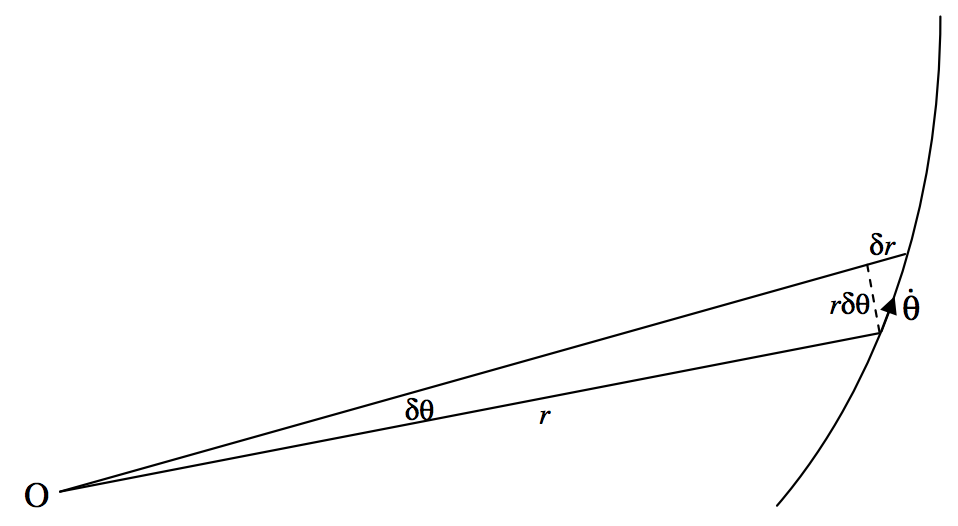
\(\text{FIGURE IX.1}\)
In figure \(\text{IX.1}\), a particle of mass \(m\) is moving in some sort of trajectory in which the only force on it is directed towards or away from the point \(\text{O}\). At some time, its polar coordinates are \((r, θ)\). At a time \(δt\) later these coordinates have increased by \(δr\) and \(δθ\).
Using the formula one half base times height for the area of a triangle, we see that the area swept out by the radius vector is approximately
\[δA = \frac{1}{2} r^2 δ θ+ \frac{1}{2} r δ θδ r. \label{9.3.1} \tag{9.3.1}\]
On dividing both sides by \(δt\) and taking the limit as \(δt → 0\), we see that the rate at which the radius vector sweeps out area is
\[\dot{A} = \frac{1}{2} r^2 \dot{θ}. \label{9.3.2} \tag{9.3.2}\]
But the angular momentum is , \(mr^2\dot{θ}\) and since this is constant, the areal speed is also constant. The areal speed, in fact, is half the angular momentum per unit mass.


