7.24: Selection rules
( \newcommand{\kernel}{\mathrm{null}\,}\)
It will be recalled that a multiplet is the totality of transitions between two terms. For example, 3P− 3Do is the multiplet connecting the two terms 3P and 3Do. Each term has three levels, and therefore there are nine ways of connecting the levels of one term with the other, each transition resulting in a line. But in fact only six of these transitions are "allowed" or "permitted", the remaining three being "forbidden". This is because of certain "selection rules", or restrictions in the way some of the quantum number can change. Likewise there are restrictions on the number of multiplets that can connect the terms of two polyads, or on the number of Zeeman components that can connect the states of two levels. In all of these situations there are selection rules that restrict certain quantum numbers from changing by other than certain amounts. In this section we shall try to understand in a qualitative way how such selection rules arise. We shall list the various selection rules, and see how this will affect the number of lines in a multiplet, or the number of components in a line.
Everyone knows that when an electric dipole oscillates it radiates an electromagnetic wave. Likewise, if a dipole, rather than periodically oscillating, suddenly undergoes a change in its electric dipole moment − for example, if the distance between two opposite electric charges suddenly changes − a pulse of electromagnetic radiation will be radiated. While the radiation from a single atom will be radiated like that of a dipole, in a gas with enormous numbers of atoms oriented in completely random directions, the radiation will appear isotropic.
One reasonable way of explaining how an atom radiates a pulse (a quantum) of electromagnetic radiation when it changes from one state to another is that its dipole moment changes, and the energy radiated is related to the change in its dipole moment. Indeed in quantum mechanics, the amount of energy radiated when an atom changes from one state to another is determined by the square of a quantity known as the transition moment:
∫ψ∗fμψidτ.
Here dτ is the usual volume element, and ψI is the wavefunction of the initial state. μ is the dipole moment operator, which depends on the positions of all the electrons in the atom. ψ∗f is the conjugate of the wavefunction of the final state. Those who have lots of practice in performing such calculations are experienced enough to know that the effect of the dipole moment operator is merely to produce a similar wavefunction with perhaps some changes in the quantum numbers. Therefore, in order to save writing out the complete expression for the wavefunction in full, they merely list the quantum numbers of the initial wavefunction in a ket, and of the conjugate of the final function in a bra, thus:
⟨L′S′J′M′|μ|LSJM⟩.
Again, those who do such calculations daily for a living soon recognize, from the very symmetries of the wavefunctions (group theory) and without having to worry greatly about the details of the functions, that this transition moment is zero unless there are certain relations between the initial and final quantum numbers. It is those transitions that result in a nonzero transition moment that are "allowed". If the transition moment is zero, which it is except for certain combinations of initial and final quantum numbers, the transition is "forbidden".
For example, if we are discussing the possible Zeeman components of a line, the only "allowed" transitions - i.e. the only nonzero transition moments - are those in which the initial and final values of M are either equal or differ by ±1. We say that the "selection rule" for the Zeeman effect is . ΔM=0, ±1 We already took account of this restriction in drawing figures VII.1 and VII.2. In the former, instead of 15 possible components, there are only nine with nonzero transition moments and which satisfy the selection rule, and in figure VII.2 there are only six rather than eight.
Actually, when observing the Zeeman effect, if we view the light from a direction perpendicular to the magnetic field, we see that the components with ΔM=0 are plane polarized parallel to the magnetic field, and are called the p-components, and the ones with ΔM=±1 are plane polarized perpendicular to the magnetic field, and are called the s-components (German senkrecht - perpendicular). (It may appear that the symbols s and p, especially the former, are by now doing more than their fair share of work.) If the spectrum is viewed from a direction along the magnetic field, the s-components will be found to be circularly polarized in opposite senses, while the p-components are not visible at all.
Just as the number of Zeeman components of a line is limited by the selection rule ΔM=0,±1 in a similar manner the number of possible lines in a multiplet is limited by a selection rule ΔJ=0,±1 (0↔0 forbidden). I already mentioned that a 3P− 3Do multiplet has just six lines rather than nine. Figure VII.3 shows the possible transitions. (Unlike figures VII.1 and VII.2, in which the horizontal scale was linear in wavelength with wavelength increasing to the right, the horizontal scale in figure VII.3 has no significance.)
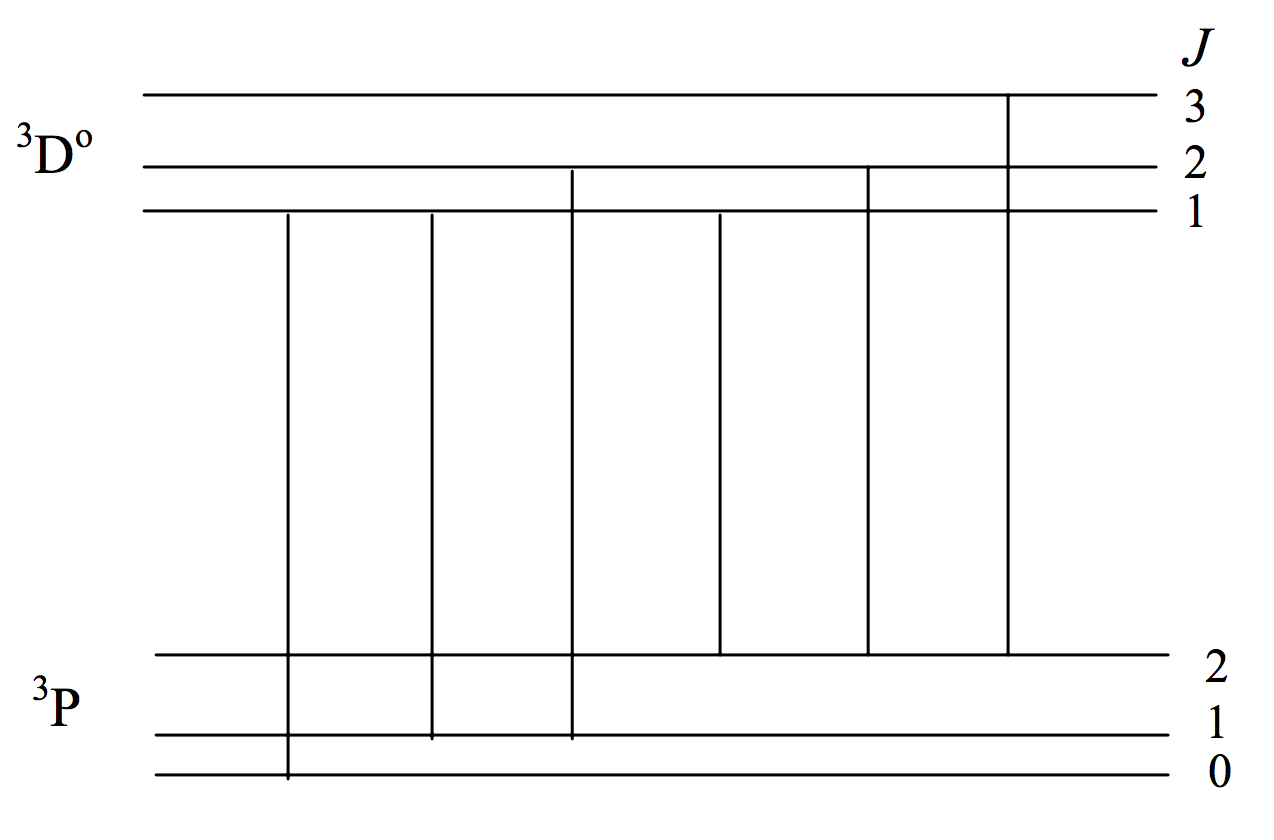
FIGURE VII.3
It may be that a line, or a component, is forbidden to dipole radiation and that, if µ is the electric dipole moment operator, the transition moment is zero. However, if we substitute for the dipole moment operator the operator for electric quadrupole or magnetic dipole moment, the transition moment is not zero. In that case a transition that is forbidden to electric dipole (E1) radiation may be permitted to electric quadrupole (E2) or magnetic dipole (M1) radiation. E2 and M1 transitions are very weak and are rarely observed under laboratory conditions (though they occur in astronomical sources for reasons that will be explained later). Therefore lines that are forbidden to electric dipole radiation are generally referred to merely as "forbidden" lines - even though they are not actually forbidden to E2 or M1 radiation. The carrier (atom) for a forbidden line is often written in brackets. For example, there is an E2 line in the spectrum of the aurora at 557.7 nm arising from the neutral oxygen atom, so the line is said to be a line of [O I].
Some multiplets are forbidden to electric dipole radiation only if the terms concerned conform strictly to LS-coupling, but may be allowed for electric dipole radiation if there are departures from LS-coupling. Such transitions are "semi-forbidden", and the carrier is sometimes written between a bracket and a parenthesis. Thus there is a semi-forbidden line at 345.3 nm due to [Al I). For LS-coupling, electric dipole radiation is allowed only if ΔS=0. That is to say, transitions are allowed between two triplet terms, or between two singlet terms, but not between a triplet or a singlet. (In this connection I am referring to a 3S term as a "triplet" term, even though it has just one level.) Not everyone uses this bracket-parenthesis convention.
In the neutral helium atom, there are singlet terms and triplet terms. LS-coupling is the norm, and, because of this, there are no transitions between any of the singlet terms and a triplet term. Indeed, it is as if there are two entirely independent sets of terms and two spectra, and indeed the singlet terms and the triplet terms are sometimes referred to as "para-helium" and "ortho-helium" respectively. Under such circumstances it is difficult (or impossible in the absence of additional independent evidence) to know the relative energies of the triplet and singlet terms, or to know which is the ground term of the atom − although we do now know that the ground term of helium is a 3S term.
Neutral calcium also has a set of singlet terms and a set of triplet terms, but there are departures from LS-coupling, and there are multiplets that connect singlet with triplet terms and vice versa. Such multiplets are called "intercombination" or "intersystem" multiplets. For example the line at 657.3 nm is a member of a 1S− 3Po multiplet of [Ca I).
Here is a list of the various selection rules I can think of. I haven’t included nuclear spin, but you may deduce what the rules are, given that the coupling between electron angular momentum and nuclear spin is generally pure JI-coupling (analogous to LS-coupling).
For Electric Dipole Transitions. Transitions take place between terms of different configurations, such that the l-value of one electron must change by ±1. It follows that allowed transitions are between terms of opposite parity. Lines within a multiplet are subject to the selection rule ΔJ=0, ±1, except that 0 to 0 is forbidden. (These rules break down for electric dipole radiation in the presence of a strong external electric field, which need not concern us here, but needs to be considered with respect to the Stark effect.) Zeeman components of a line are subject to the selection rule δM=0,±1.
For LS-coupling, there are the following additional constraints. ΔS=0; that is to say, intersystem transitions are forbidden to electric dipole radiation. They are "semi-forbidden". ΔL=0, ±1, except that 0 to 0 is forbidden. Thus S− So, S− Do, P− Fo multiplets would all be indicative of departures from LS-coupling. Transitions must also take place between terms of common parentage.
For Magnetic Dipole Transitions. Transitions take place between terms of a single configuration, and hence between terms of the same parity. Lines within a multiplet are subject to the selection rule ΔJ=0, ±1, except that 0 to 0 is forbidden. Zeeman components of a line are subject to the selection rule ΔM=0, ±1, except that ΔJ and ΔM cannot both be zero.
For LS-coupling there are the additional constraints ΔS=0 and ΔL=0.
For Electric Quadrupole Transitions. Transitions take place either between terms of the same configuration or between configurations in which the l-value of one electron changes by ±2. In either case this implies that transitions take place between terms of the same parity. Lines within a multiplet are subject to the selection rule ΔJ=0, ±1, ±2, except that 0−0, 12−12, 0−1 and 1−0 are forbidden. This implies that J′+J′′ must be at least 2. Zeeman components of a line are subject to the selection rule ΔM=0, ±1, ±2.
For LS-coupling there are the additional constraints ΔS=0 and ΔL=0, ±1, ±2, except that ΔL=0−0, 0−1, 1−0 are forbidden. Transitions must also take place between terms of common parentage.
Exercise. In section 7.16 I listed the first ten levels for the hydrogen atom - i.e. the levels in the first three shells. I also asserted that Hα comprises three transition arrays, three multiplets, seven lines and an unspecified number of Zeeman components. Now that you are familiar with selection rules, you are in a position to verify this. Therefore, as an exercise, list all of the arrays, multiplets and lines comprising Hα. (You should assume LS-coupling; obviously with just one electron there is no distinction between LS- and jj-coupling.) For example, 2p−3d is one array. 2p 2Po−3d 2D is a multiplet. 2p 2Po32−3d 2D52 is a line. In the table in section 7.16, I have listed the statistical weight of each level. For each level, list the possible M values, and then, using the Zeeman selection rules, determine how many Zeeman components there are for each level, and therefore for Hα as a whole. How many of the Zeeman components have distinct wavelengths?
In the above exercise, perhaps you ignored the effect of nuclear spin. Now include nuclear spin (I=1/2). You will see now that each of the eight levels involved in the formation of Hα is split into two hyperfine levels with different values of F. Now, how many hyperfine and Zeeman are there?
Now answer the same questions with deuterium. One might hope that the deuterium nucleus (the "deuteron") has zero nuclear spin - but no such luck, for the spin of the deuteron is I=1. Thus most of the levels are composed of three hyperfine levels. (Why did I say "most"? Some of the levels have just two hyperfine levels, don't they? Do you see why?) How many hyperfine and Zeeman components are allowed by the selection rules?
Of course, natural hydrogen includes both 1H and a very small amount of 2H, and the spectra of both will be exhibited. Truly Hα is a much more complicated "line" than we envisaged in section 7.3! To add to the complication, we must not forget that under terrestrial conditions, hydrogen is molecular, and there are three possible isotopomers - H2, HD and D2 - and those familiar with molecular spectra will recall that there are obvious differences between the spectra of homonuclear and heteronuclear molecules. One could clearly spend a lifetime studying the spectrum of hydrogen!


