7.14: States, Levels, Terms, Polyads, etc.

An electron configuration is a listing of the number of electrons in each shell and the orbital angular momentum of each. We gave an example of the lowest electron configuration of \(\text{Cu I}\) in section 7.12.

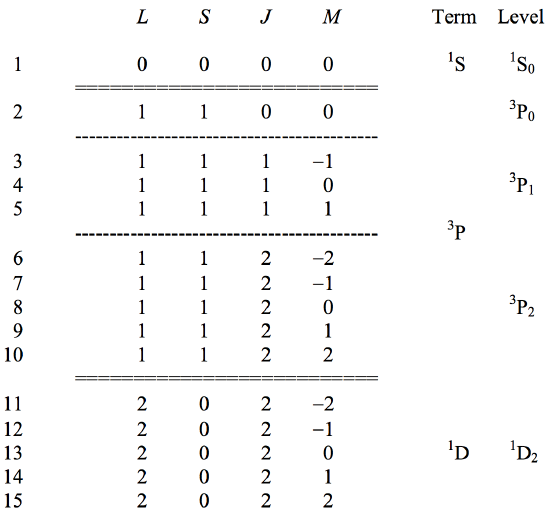
For a given electron configuration it is possible to predict the several (many) eigenfunctions that can exist. I shall not show how to do this, but I shall list, by way of example, the quantum numbers of the eigenfunctions that can arise from two \(p\) electrons in the same shell (i.e. having the same principal quantum number \(n\).) If two \(p\) electrons are in the same shell, they are referred to as "equivalent" \(p\)-electrons, and the electron configuration is written \(p^2\). If they are in different shells (have different \(n\)) they are "nonequivalent" electrons, and the configuration is written \(p.p\). We are going to deal, then with two equivalent \(p\)-electrons, \(p^2\). Without proof, I now list the 15 possible combinations of quantum numbers \(LSJM\) of the 15 states that arise from this configuration.

	L	S	J	M	Term	Level
1	0	0	0	0	\(^1S\)	\(^1S_0\)
2	1	1	0	0		\(^3P_0\)
3	1	1	1	-1
4	1	1	1	0		\(^3P_1\)
5	1	1	1	1
6	1	1	2	-2	\(^3P\)
7	1	1	2	-1
8	1	1	2	0		\(^3P_2\)
9	1	1	2	1
10	1	1	2	2
11	2	0	2	-2
12	2	0	2	-1
13	2	0	2	0	\(^1D\)	\(^1D_2\)
14	2	0	2	1
15	2	0	2	2

In principle we could write out in full the complete wavefunction for each of these states, though it is simpler to write the wavefunction in the form of a \(ket |LSJM\rangle\), in which we merely list the quantum numbers - because most of the operators encountered in quantum mechanics when acting upon the spherical harmonics result in similar functions with at most a change in the quantum numbers. Thus the wavefunction for the first state in the list above would be written merely as \(|0000\rangle\), and the wavefunction for the last one would be written \(|2022\rangle\).

The totality of states with the same values of \(L\) and \(S\) is called a term. Thus the nine states 2 to 10 all have the same values of \(L\) and \(S\) and they comprise a term. The five states 11 to 15 also have the same values of \(L\) and \(S\), and they also comprise a term. There is only one state with \(L = 0\) and \(S = 0\). This is a term that contains only one state.

A term is denoted by the letter \(\text{S, P, D, F, G, H, I, K}\),… according to whether its \(L\)-value is \(0, 1, 2, 3, 4, 5, 6, 7\),…. The value of \(2S+1\) is written as an upper left superscript. Thus the three terms are as follows:

\begin{array}{l c c}
\text{State 1:} && ^1 \text{S} \\
\text{States 2 - 10:} && ^3 \text{P} \\
\text{States 11 - 15}: && ^1 \text{D} \\
\end{array}

These terms are generally pronounced "singlet-S, triplet-P , singlet-D".

The totality of states with the same values of \(L\), \(S\), and \(J\) is called a level. Thus the term \(^3 \text{P}\) has three levels, denoted by \(^3 \text{P}_0\), \(^3 \text{P}_1\) and \(^3 \text{P}_2\), in which the value of \(J\) is written as a bottom right subscript.

Except in the presence of an external magnetic or electric field, all states belonging to a given level have the same energy, and on an energy level diagram they would appear as a single horizontal line. The number of states in a given level is \(2J+1\) and this is called the degeneracy \(d\) of the level.

The number of levels in a term (see discussion following equation 7.13.3) is \(2\text{min} \left\{ L,S \right\} + 1\). This is called the multiplicity \(g\) of the term. In all of the terms discussed above arising from the configuration \(p^2\), \(S\) is less than or equal to \(L\), and therefore the multiplicity of these terms is \(2S+1\), which is equal to the upper left superscript. Consider, however, the terms \(^3 \text{S}\) and \(^5 \text{P}\), which occur in some other configurations. In these two cases, \(L < S\), so the multiplicity is \(2L+1\). For \(^3 S\) we have \(S = 1\) and \(L = 0\); the multiplicity is \(1\) and the only level in the term has \(J = 1\). For \(^5 \text{P}\), we have \(S = 2\) and \(L = 1\); the multiplicity is \(3\) and the three levels are \(^5 \text{P}_{1,2,3}\). Nevertheless it is customary to pronounce these terms "triplet-S, quintet-P".

The statistical weight \(\varpi\) of a level or a term is the number of states in it. The statistical weight of a level is the same as its degeneracy, and is \(2J+1\). The statistical weight of a term is the sum of the degeneracies of its constituent levels, and is \((2L +1)(2S +1)\), regardless of the relative sizes of \(L\) and \(S\). You should verify this for each of the levels and terms in the configuration \(p^2\). The symbol \(\varpi\), by the way, is a form of the Greek letter pi, and resembles the way in which pi is written in handwriting.

Exercise. Show that \(\sum\limits_{|L-S|}^{L+S}{(2J+1)}=(2L+1)(2S+1)\) regardless of the relative sizes of \(L\) and \(S\).

The reader might note that not all authors retain the distinction between degeneracy, multiplicity and statistical weight, or the symbols I am using to represent them. In particular, the symbol \(g\) is (regrettably) often used for the statistical weight or degeneracy of a level. It is not always clear what concept is being represented by a given symbol, and it is important in your own writing always to make it clear yourself and never to assume that your readers will understand what you intend if you not make it clear. Please also do not refer to the upper left superscript of a term as its "multiplicity". The multiplicity is \(2 \text{min}\left\{L , S\right\} + 1\); the upper left superscript is \(2S+1\).

Parentage. We'll try to understand this word by means of an example, and we'll consider the neutral vanadium atom. The spectrum of vanadium is quite complex, and there are many lowlying terms. For example, among the many terms whose term values are within \(3 \ \mu \text{m}^{-1}\) of the ground level are four \(^6 \text{D}\) terms. These are terms with \(S = \frac{5}{2}\), \(L = 2\) The multiplicity of such a term is \(5\), the \(J\)-values being \(\frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \frac{7}{2}, \frac{9}{2}\). The ground configuration of \(\text{V}_\text{I}\) is \(KL3s^2 3p^6 3d^3 4s^2\). Here I have abbreviated the first ten electrons in the configuration with the letters \(KL\), to indicate full \(K\) and \(L\) shells. In fact in the present discussion, I am not going to be specially interested in the first \(18\) electrons, and I am going to indicate the ground configuration merely by \(3d^3 4s^2\). In fact, none of the four \(^6 \text{D}\) terms under discussion comes from this configuration. They all come from excited configurations. Specifically, in order of increasing energy, the configurations of these four \(^6 \text{D}\) terms are:

\begin{array}{l}
3d^4 4s \\
3d^3 4s 4p \\
3d^4 4p \\
3d^3 4s 4p \\
\end{array}

You will notice that two of them (the second and fourth) arise from the same configuration.

Let us consider how the several \(^6 \text{D}\) terms arise. Consider the first of them. The configuration \(3d^4\) of \(\text{Ti} \ _\text{I}\) (titanium is the element just before vanadium in the periodic table) gives rise to a great many terms (I believe it gives rise to \(16\) terms). In particular there is a \(^5 \text{D}\) term. If you now add a \(4s\) electron (to turn titanium into vanadium) to the \(^5 \text{D}\) term of \(\text{Ti} \ _\text{I}\), this gives rise to two \(\text{V} \ _\text{I}\) terms, one of which is the first of our \(^6 \text{D}\) terms of interest. The \(^5 \text{D}\) term of the \(\text{Ti} \ _\text{I}\) \(3d^4\) configuration is called the parent of this term, and, to make this clear, the configuration of the first \(\text{V} \ _\text{I}\) \(^6 \text{D}\) term is written

\[3d^4 \left( ^5 \text{D} \right) 4s\]

In a similar manner, the configurations of the other three \(^6 \text{D}\) terms of \(\text{V} \ _\text{I}\) with their parents indicated are

\begin{array}{l}
3d^3 4s \left(^5 \text{F} \right) 4p \\
3d^4 \left( ^5 \text{D} \right) 4p \\
3d^3 4s \left( ^5 \text{P} \right) 4p \\
\end{array}

Many terms of \(\text{V} \ _\text{I}\) have the same parent. Thus \(3d^4 \left(^5 \text{D} \right) \) is parent to eight terms in the lowest \(3 \ \mu \text{m}^{-1}\) of term value. The totality of terms having the same parent is called a polyad.

Parity. The wavefunction that describes a particular term has the property that if it is inverted through the origin (this means, in spherical coordinates, that \(\theta\) and \(\phi\) are replaced by \(\pi−\theta\) and \(\pi+\phi\) respectively) the wavefunction is either unchanged or just changes in sign. In the former case the term is said to be of even parity; in the latter case it is of odd parity. This may sound like a rather obscure wavemechanical nicety, bit it is of sufficient importance to a working spectroscopist that he or she needs to know the parity of each term. Because of this it is usual (in fact essential) to indicate a term of odd parity by means of the upper right superscript \(^{\text{o}}\). Terms of odd parity, for example, might be written \(^3 \text{P}^{\text{o}}\), \(^4 \text{S}^{\text{o}}\), etc. It is easy to know (if not to understand why) a given term has odd or even parity. If the (scalar) sum of the \(l\)-values of the configuration from which a term arises is even, the parity is even; if it is odd, the parity is odd. When we earlier considered the terms arising from \(p^2\), all the terms had even parity, because the sum of the \(l\)-values of the two \(p\) electrons is \(2\).

The reason why a working spectroscopist needs to know the parity of a term will become evident later in section 7.24 on selection rules.