1: A Review of Coordinates
- Page ID
- 3598
Latitude and Longitude (Fixed to Earth)
On Earth, one way to describe a location is with a coordinate system which is fixed to the Earth's surface.
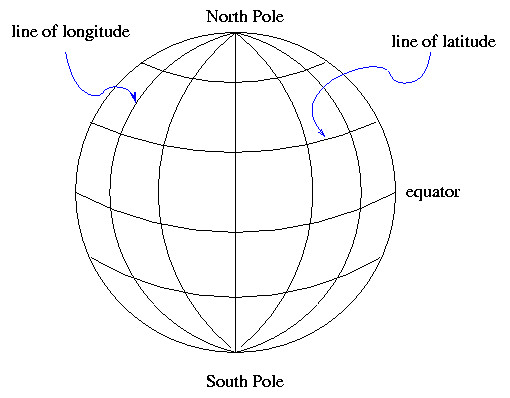
The system is oriented by the spin axis of the Earth, and has special points at the North and South Poles. We use lines of latitude and longitude to demarcate the surface. It's obvious that latitude is measured away from the equator. But where is the starting point for longitude? There is no "obvious" choice. After a lot of dickering, European nations finally decided to use the location of the Greenwich Observatory in England as the starting point for longitude.
There are several ways to specify a location -- for example, that of the RIT Observatory. One can use degrees:
latitude 43.0758 degrees North, longitude 77.6647 degrees West of Greenwich
Or degrees, minutes and seconds:
latitude 43:04:33 North, longitude 77:39:53 West
Or, in the case of longitude, one can measure in time zones. The sun will set at the RIT Observatory about 5 hours and 11 minutes later than it does at Greenwich, so one could say
latitude 43:04:33 North, longitude 05 hours 11 minutes West
This ought to be pretty familiar. Think you understand it? Then try applying your knowledge of latitude and longitude to solve a simple little problem:
Finding the distance between two locations on Earth is a first step in calculating the distance to other objects in the solar system via parallax....
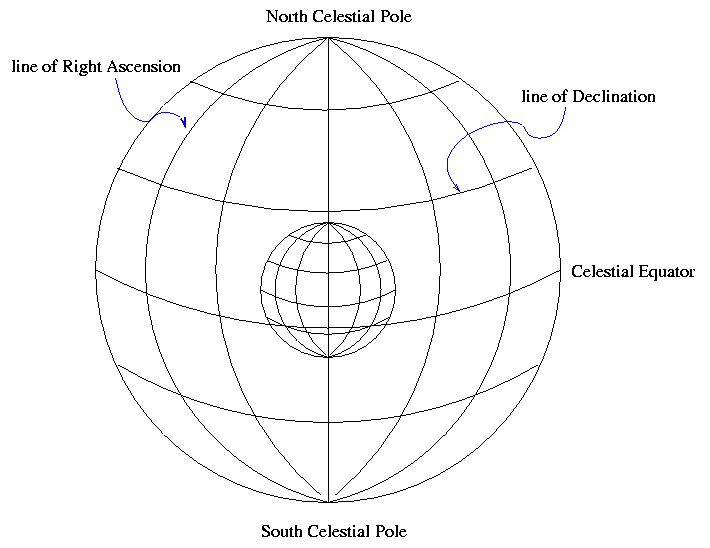
Right Ascension and Declination (Fixed to Sky)
On can make a similar coordinate system which is "fixed to the sky". Once again, we use the Earth's rotation axis to orient the coordinates. There are two special places, the North and South Celestial Poles. As the Earth rotates (to the East), the celestial sphere appears to rotate (to the West). Stars appear to move in circles: small ones near the celestial poles, and large ones close to the celestial equator:

The North Star and circumpolar stars in a photograph with a long shutter speed of several hours. Note that the stars near the celestial pole make less of a trail with the long exposure. (CC-SA-BY 3.0; LCGS Russ)
We again use two orthogonal coordinates to describe a position:
- Declination, like a celestial latitude
- Right Ascension, like a celestial longitude
As with latitude, Declination is measured away from the celestial equator. But there is again no obvious choice for the starting point of the other set of coordinates. Where should we start counting Right Ascension? The rather arbitrary choice made by astronomers long ago was to pick the point at which the Sun appears to cross the celestial equator from South to North as it moves through the sky during the course of a year. We call that point the "vernal equinox".
Once again, there are several ways to express a location. The star Sirius, for example, can be described as at
Right Ascension 101.287 degrees, Declination -16.716 degrees
We can also express the Declination in Degrees:ArcMinutes:ArcSeconds, just as we do for latitude; and, as usual, there are 360 degrees around a full circle. For Right Ascension, astronomers always use the convention of Hours:Minutes:Seconds. There are 24 hours of RA around a circle in the sky, because it takes 24 hours for the Sun to move all the way from sunrise to the next sunrise.
Thus, 1 hour of RA equals 15 degrees of RA. Along the celestial equator, those 15 "degrees of RA" are the same as 15 ordinary degrees. That is, a star located at (RA = 6 hours, Dec = 0 degrees) would be exactly 15 degrees away from a star located at (RA = 7 hours, Dec = 0 degrees). As one moves away from the celestial equator and toward the poles, the lines of RA converge:
For points off the celestial equator, the real distance in the RA direction is smaller by a factor of cos(Dec).
What is the angular separation between two stars at (RA = 6 hours, Dec = +60 degrees) and (RA = 7 hours, Dec = +60 degrees)?
Converting Sirius' position into sexigesimal form, we find
Right Ascension 06:45:09, Declination -16:42:58
- the Right Ascension is 6 hours, 45 minutes, 09 seconds
- the Declination is -16 degrees, 42 arcminutes, 58 arcseconds
one degree is divided into 60 arcminutes
- one arcminute is divided into 60 arcseconds. Therefore, there are 3600 arcseconds in one degree
- one hour of time (equal to 15 degrees at the celestial equator) is divided into 60 minutes of time
- one minute of time (equal to 15 arcminutes at the celestial equator) is divided into 60 seconds of time. Therefore, there are 3600 seconds of time in one hour of time
- one second of time is equal to 15 arcseconds at the celestial equator
- one minute of time (equal to 15 arcminutes at the celestial equator) is divided into 60 seconds of time. Therefore, there are 3600 seconds of time in one hour of time
Spherical Trigonometry
You've learned trigonometry in high school: sines, cosines, the Pythagorean Theorem, and all that jazz. However, unless you went to a really good high school, you probably restricted your calculations to planar geometry. Unfortunately, the sky is not a plane. We measure positions and coordinates on the inner surface of an imaginary sphere. That means that the old rules don't always work anymore. The subject of spherical trigonometry is not a simple one, but, in this course, we will only peek into it.
Given two vectors, \(\vec{a}\) and \(\vec{b}\), what is the distance between them? On a plane, we can break up each vector into its components and use the Pythagorean theorem:
\[ \text{distance} = \sqrt{(a_x-b_x)^2 + (a_y - b_y)^2}\]
Along the surface of the celestial sphere, if we want to find the angular distance between two points \(\vec{a}\) and \(\vec{b}\), we need to use the law of cosines. In the usual case, the two points are expressed in Right Ascension (\(α\)) and Declination (\(δ\)), like so:
\[ a = (\alpha_a, \delta_a)\]
\[ b = (\alpha_b, \delta_b)\]
In this case, the law of cosines becomes
\[ \cos (\gamma) = \cos (90° - \delta_a) \cos (90° - \delta_b) + \sin (90° - \delta_a) \sin (90° - \delta_b) \cos (\alpha_a - \alpha_b)\]
which gives us the cosine of the desired angular distance \(γ\).
If we are interested in very small angular distances on the sky -- the separation between the two components of a binary star, for example, or the distance between two of the moons of Jupiter -- then there are two common approximations. First, if we start with the RA and Dec coordinates of the two points, we can make a pseudo-Pythagorean formula; all we have to do is correct the difference in Right Ascension with the cosine of the Declination.
\[ \gamma \approx \sqrt{[(\alpha_a-\alpha_b)\cos (\delta_a)]^2 + (\delta_a - \delta_b)^2} \label{Pyth} \]
Second, if we start with a picture of some very small region of the sky, together with an indication of the scale in arcseconds, like below, then we can
- pick any two orthogonal directions on the picture
- measure the separation (in arcseconds) in each direction
- use the good old Pythagorean formula (Equation \(\ref{Pyth}\))

Quasar 3C 273, with its jet. Image by Chandra X-ray Observatory. (Public domain; NASA)


