2.2: Collisions and Decays
- Page ID
- 9714
A neutral pion (rest energy 135 MeV) moving at 0.7c decays into a pair of photons. The photons each travel at the same angle from the initial pion velocity. Find this angle and the energy of each photon.
Any process that occurs in nature must obey energy and momentum conservation. To analyze this particle decay, apply both conservation laws to the process.
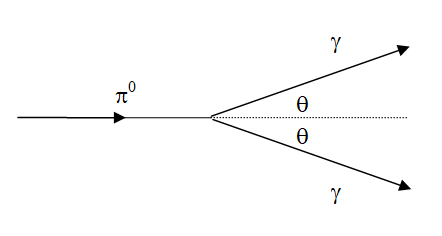
First, find the Lorentz factor for the pion.
\[ \begin{align} \gamma &= \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}} \\[5pt] &= \dfrac{1}{\sqrt{1 - \dfrac{(0.7 c)^2}{c^2}}} \\[5pt] &= 1.4 \end{align}\]
Applying energy conservation yields:
The two photons must have the same energy since they travel in the same direction relative to the initial pion velocity. This is the only way that momentum in this perpendicular direction can be conserved.
Applying momentum conservation (actually conservation of “pc”) along the initial direction of travel and using the relationship yields:
The photons each travel at 45.60 from the direction of the pions initial path.
Collisions and Decays II
A photon of energy 500 keV scatters from an electron at rest. The photon is redirected to an angle of 35° from its initial direction of travel. Find the energy of the scattered photon and the angle and energy of the scattered electron.
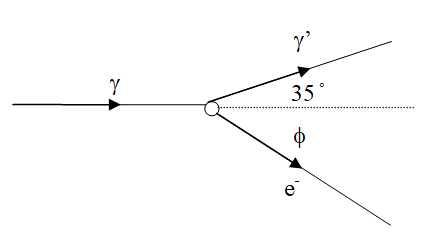
To analyze, apply energy conservation:
\[ E_{photon} + E_{electron} = E_{photon}' + E'_{electron}\]
\[ 500 + 511 = E_{photon}' + E'_{electron}\]
\[ 1011 = E_{photon}' + E'_{electron}\]
note that the electron initially has only rest energy.
Apply x-momentum conservation (and use \(pc = \sqrt{ E_{total}^2 - (mc^2)^2} \)):
Apply y-momentum conservation:
This yields three equations with the requested three unknowns (\(E’_{photon}\), \(E’_{electron}\), and \(\phi\)).
If you enjoy algebra, solve this system of equations by hand. If you have better things to do with your life, use a solver to find:
\[ E'_{photon} = 425\; keV\]
\[E'_{photon} = 586 \, keV\]
\[ \phi = 58.1°\]


