7.2: Air Resistance Proportional to the Speed
( \newcommand{\kernel}{\mathrm{null}\,}\)
As in the previous section, I shall write the x-component of the equation of motion, and of the first and second time integrals, in the left hand column, and the y-component in the right-hand column. The x-component of the air resistance per unit mass is γ˙x and the y-component is γ˙y. Here γ is the damping constant, defined in Section 6.3. The x- and y-components of the initial velocity are, respectively, V0cosα and V0sinα. It should be readily seen that the equations of motion and their time integrals are as follows:
| Horizontal | Vertical | |
|---|---|---|
| ¨x=−γ˙x | ¨y=−g−γ˙y | 7.2.1a,b |
| ˙x=u=V0cosα.e−γt | ˙y=v=V0sinαe−γt−ˆv(1−eγt)whereˆv=g/γ | 7.2.2a,b |
| x=x∞(1−e−γt)where x∞=V0cosαγ | y=1γ(V0sinα+ˆv)(1−e−γt)−ˆvt | 7.2.3a,b |
(In case it is not "readily seen", for the horizontal motion refer to Chapter 6, Section 3, especially Equations 6.3.2, 6.3.3 and 6.3.5, and for the vertical motion refer to Chapter 6, Section 3b, especially Equations 6.3.24, 6.3.25 and 6.3.27.) It will be seen that, as t→∞, u→0, v→−ˆv, x→x∞. The xy-equation to the trajectory is the t-eliminant of Equations 6.2.3a and 6.2.3b. After a small amount of algebra this is found to be:
y=x(V0sinα+ˆv)V0cosα+ˆvγln(1−xx∞).
The range on a horizontal plane is found by setting y = 0, to obtain either
x=−Aln(1−xx∞)
or
x=x∞(1−e−xA),
where
A=ˆvV0cosαγ(V0sinα+ˆv),x∞=V0cosαγ
and
ˆv=gγ.
Suppose
- V0 = 20 ms-1
- α = 50∘
- g =9.8 ms-2
- γ =1.96s-1 (∴ˆv=5 ms−1)
Then A =1.613 870 65 m
and x∞ = 6.55905724 m.
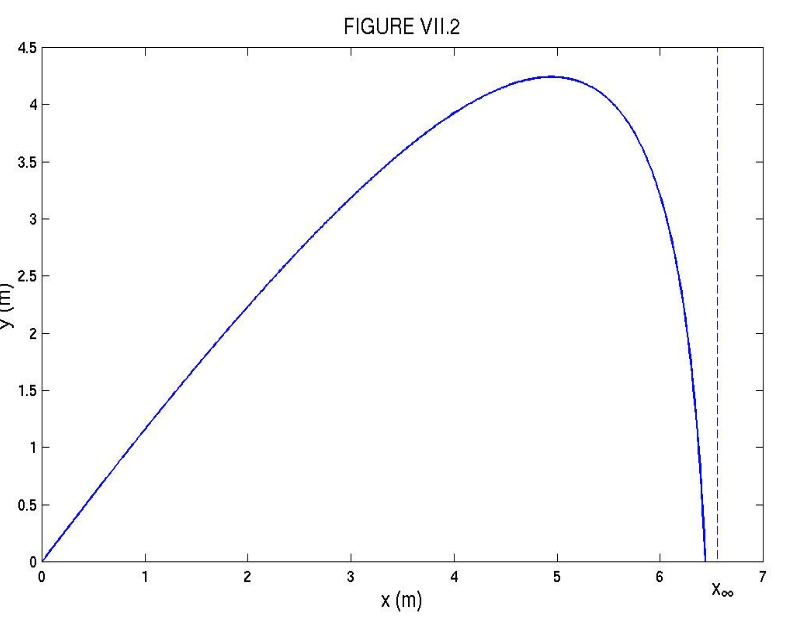
Try to find the range on the horizontal plane, using either Equation 7.2.5 or 7.2.6, to nine significant figures. Which equation works best? Newton-Raphson may fail with a stupid first guess - but it should not be difficult to make a fairly intelligent first guess. I should not tell you, but figure VII.2 was calculated using the data of this example.
I make the answer 6.437 584 2 m.
Here’s a more difficult problem.
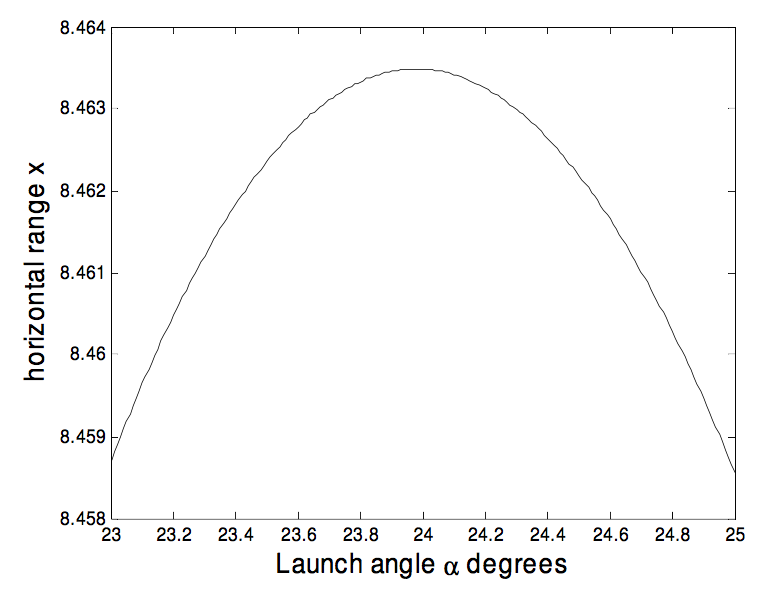
It is well known that, in the absence of air resistance, the maximum range on the horizontal plane is effected by choosing the initial launch elevation to be α = 45∘. What if there is air resistance, with damping constant γ? What, then, should be the angle of launch to achieve the greatest range on the horizontal plane? Given Equation 7.2.6, x=x∞(1−e−xA), for what value of α is x greatest?
Solution
Equation 7.2.6, written in full, is
x=V0cosαγ[1−exp(−γ(V0sinα+ˆv)xˆvV0cosα)].
This can be written
x=acosα[1−exp(−(bsinα+1)xacosα)],
where a=V0γ and b=V0ˆv=γV0g. We have to find for what value of α is x greatest. It seems a simple enough problem, but at the moment I can’t find a good way of solving it. If anyone has a clue, let me know (jtatum@uvic.ca). In the meantime, the best I can offer is, for our particular numerical example, to calculate the range, x, for several values of α and see where it goes through a maximum. For our particular numerical example, a = 10.204 081 63 m and b = 4. Here is a graph of range versus launch angle, for an initial speed of 20 ms−1. A launch angle of about 23∘ 59′ gives a range of about 8.4635 m. For a given γ and g, the optimum launch angle depends on the launch speed V0. Is this intuitively obvious?