20.2.2: Angle of Contact
- Page ID
- 8528
When a static quantity of liquid is in contact with an impermeable solid surface, it generally rests so that there is a characteristic angle (measured in the liquid) between the surface of the liquid and the surface of the solid. This angle is the angle of contact, and is shown as the angle \(\theta \) is Figure XX.3. Figure XX.3(a) shows an acute angle of contact, in which the liquid spreads out a little and "wets" the surface. Figure XX.3(b) shows an obtuse angle of contact, in which the liquid "bunches up", and does not wet the surface, rather like drops of mercury on most surfaces, or drops of water on the surface of a car that has been freshly waxed. In many cases the angle of contact is close to either \( 0 ° \) or \( 180 ° \), although it will be appreciated that if \( \theta \) were exactly zero, the liquid would spread
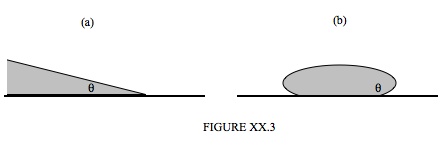
out in an infinitesimally thin layer to cover or "wet" the entire surface; and if it were exactly \( 180 ° \), the liquid, in the absence of other forces (such as its weight!), would form a spherical globule in contact with the surface only at a single point. The angle of contact is determined by the nature of both surfaces, and is very sensitive to any surface contamination. In order to wet a surface, water may need to be helped by a small amount of wetting agent or detergent; only a small amount is necessary, because only the surface, and not the bulk, of the liquid is involved. The chemical nature of wetting agents and detergents is beyond the scope of these notes (i.e. it is beyond my scope!), but how the angle of contact depends on the surface tension provides a useful example of the technique of virtual work (see Section 9.4 of Chapter 9).
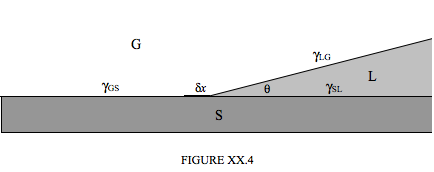
Figure XX.4 represents a liquid, L, (e.g. water) in contact with a solid, S, (e.g. glass) and a gas, G, (e.g. air). The angle of contact is \( \theta \), and the surface tensions (energy per unit area, or, for those who are versed in thermodynamics, the Gibbs free energy per unit area) of the three interfaces are as shown. We'll suppose that the three media extend for a distance \(l\) at right angles to the plane of the paper (or computer screen). The three phases are in equilibrium. Now, if we move the SLG boundary to the left by a distance \( \delta x\), we create a new area \( l \delta x \) of SL interface and a new area \( l \cos \theta \delta x \) of LG interface, while we lose an area \( l \delta x \) of GS interface. The work done on the system is therefore \( \gamma_{SL} l \delta x + \gamma_{LG}l \cos \theta \delta x - \gamma_{GS} l \delta x \). By the principle of virtual work, this is zero, and therefore
\[ \cos \theta = \dfrac{\gamma_{GS} - \gamma_{SL}}{\gamma_{LG}} . \tag{20.2.5}\label{eq:20.2.5} \]
The angle of contact is acute or obtuse, according to whether \( \gamma_{GS} \) is greater than or less than \( \gamma_{SL} \).


