20.4.1: Poiseuille's Law
- Page ID
- 8532
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Poiseuille’s law tells you how the rate of nonturbulent flow of a liquid through a cylindrical pipe depends on the viscosity of the liquid, the radius of the pipe, and the pressure gradient. If all else fails, you can at least try dimensional analysis. Assume that the rate of flow of liquid (in cubic metres per second) is proportional to \( \eta^\alpha a^\beta \left( \frac{dP}{dx}\right)^ \gamma, \) and show by dimensional analysis that \(\alpha = −1, \beta = −4 \) and \(\gamma = 1\), which shows that the rate of flow is very sensitive to the radius of the pipe. That \( \beta = −4 \) tells you that if your arteries are at all constricted, even by a little bit, you had better watch out. Gas flow is more complicated because gases are compressible, (so are liquids, but not by much), but \( \beta = −4 \) tells you that the rate at which you can pump out gas from a system depends a lot on the size of the smallest tube you have between the volume that you are trying to evacuate and the pump. Now let’s try and analyse it further.
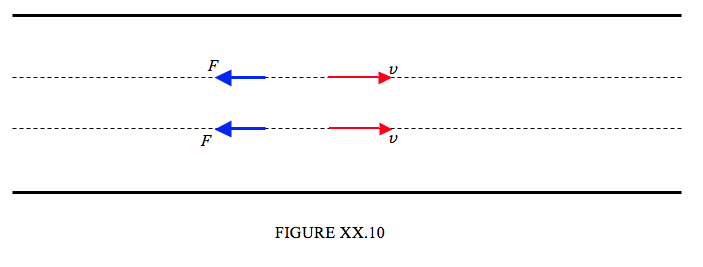
Figure XX.10 represents a pipe of radius \(a\) with liquid flowing to the right. At a distance \(r\) from the axis of the pipe the speed of the liquid is \(v\). The length of the pipe is \(l\), and there is a pressure gradient along the length of the pipe, the pressure at the left end being higher than the pressure at the right by \(P\). There is a velocity gradient in the pipe. The speed of the liquid along the axis of the pipe is v0, and the speed at the circumference of the pipe is zero. That is, the speed decreases from axis to circumference, so that the velocity gradient \( (dv/dr) \) is negative.
Now consider the equilibrium of the liquid inside radius \(r\). (It is in equilibrium because it is moving at constant speed.) It is being pushed forward by the pressure gradient. This rightward force is \( \pi r^2 P \). It is being dragged back by the viscous force acting on the area \( 2 \pi rl\). This leftward force is \( -2 \pi \eta lr(dv/dr) \), this expression for the leftward force being positive.
Therefore
\[ -2 \eta l \frac{dv}{dr} = Pr . \tag{20.4.1}\label{eq:20.4.1} \]
Integrate from the axis \((r = 0, v = v_0) \) to \(r\):
\[ v = v_0 - \frac{Pr^2}{4 \eta l }. \tag{20.4.2}\label{eq:20.4.2} \]
Thus the speed decreases quadratically (parabolically) as you move away from the axis. The speed is zero at the circumference, and hence the speed on the axis is
\[ v_0 =\frac{Pr^2}{4 \eta l }. \tag{20.4.3}\label{eq:20.4.3} \]
Verify the dimensions.
Now the volume flow through a cylindrical shell of radii \(r\) and \(r + dr\) is the speed times the area \( 2 \pi r dr, \), which is \( \frac{\pi r^3 dr}{2 \eta l} \), and if you integrate that through the whole pipe, from 0 to \(a\), you find that the rate of flow of liquid through the pipe (cubic metres per second) is
\[ \frac{ \pi a ^4 P }{ 8 \eta l }. \tag{20.4.4}\label{eq:20.4.4} \]
This is Poiseuille’s Law.