4.4: Angular Momentum

Conservation of momentum followed from the invariance of the Lagrangian on being displaced in arbitrary directions in space, the homogeneity of space, angular momentum conservation is the consequence of the isotropy of space—there is no preferred direction.

So angular momentum of an isolated body in space is invariant even if the body is not symmetric itself.

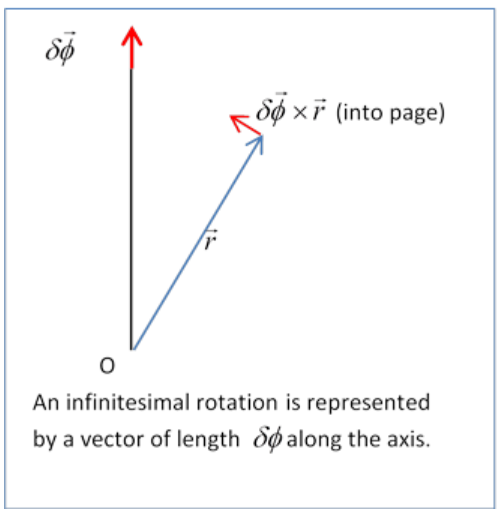
The strategy is just as before, except now instead of an infinitesimal displacement we make an infinitesimal rotation,

\begin{equation}
\delta \vec{r}=\delta \vec{\phi} \times \vec{r}
\end{equation}

and of course the velocities will also be rotated:

\begin{equation}
\delta \vec{v}=\delta \vec{\phi} \times \vec{v}
\end{equation}

We must have

\begin{equation}
\delta L=\sum_{i}\left(\frac{\partial L}{\partial \vec{r}_{i}} \cdot \delta \vec{r}_{i}+\frac{\partial L}{\partial \vec{v}_{i}} \cdot \delta \vec{v}_{i}\right)=0
\end{equation}

Now \(\begin{equation}
\partial L / \partial \vec{v}_{i}=\partial L / \partial \dot{\vec{r}}_{i}=\vec{p}_{i}
\end{equation}\) by definition, and from Lagrange’s equations

\begin{equation}
\partial L / \partial \vec{r}_{i}=(d / d t)\left(\partial L / \partial \dot{\vec{r}}_{i}\right)=\dot{\vec{p}}_{i}
\end{equation}

so the isotropy of space implies that

\begin{equation}
\sum_{i}\left(\vec{p}_{i} \cdot \delta \vec{\phi} \times \vec{r}_{i}+\vec{p}_{i} \cdot \delta \vec{\phi} \times \vec{v}_{i}\right)=0
\end{equation}

Notice the second term is identically zero anyway, since two of the three vectors in the triple product are parallel:

\begin{equation}
\left(d \vec{r}_{i} / d t\right) \times \vec{p}_{i}=\vec{v}_{i} \times m \vec{v}_{i}=0
\end{equation}

That leaves the first term. The equation can be written:

\begin{equation}
\delta \vec{\phi} \cdot \frac{d}{d t} \sum_{i} \vec{r}_{i} \times \vec{p}_{i}=0
\end{equation}

Integrating, we find that

\begin{equation}
\sum_{i} \vec{r}_{i} \times \vec{p}_{i}=\vec{L}
\end{equation}

is a constant of motion, the angular momentum.

The angular momentum of a system is different about different origins. (Think of a single moving particle.) The angular momentum in the rest frame is often called the intrinsic angular momentum, the angular momentum in a frame in which the center of mass is at position \(\begin{equation}
\vec{R} \text { and moving with velocity } \vec{V} \text { is }
\end{equation}\).

\begin{equation}
\vec{L}=\vec{L}_{\mathrm{cm} \mathrm{frame}}+\vec{R} \times \vec{P}
\end{equation}

(Exercise: check this.)

For a system of particles in a fixed external central field \(\begin{equation}
V(r)
\end{equation}\), the system is invariant with respect to rotations about that point, so angular momentum about that point is conserved. For a field “cylindrically” invariant for rotations about an axis, angular momentum about that axis is conserved.