11.1: Paths in Simple Phase Spaces - the SHO and Falling Bodies

Last updated
Save as PDF

Page ID: 29463

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Let’s first think further about paths in phase space. For example, the simple harmonic oscillator, with Hamiltonian \(\begin{equation}
H=p^{2} / 2 m+m \omega^{2} q^{2} / 2
\end{equation}\) describes circles in phase space parameterized with the variables \(\begin{equation}
(p, m \omega q)
\end{equation}\). (A more usual notation is to write the potential term as \(\begin{equation}
\frac{1}{2} k q^{2}
\end{equation}\))

Question: are these circles the only possible paths for the oscillator to follow?

Answer: yes: any other path would intersect a circle, and at that point, with both position and velocity defined, there is only one path forward (and back) in time possible, so the intersection can’t happen.

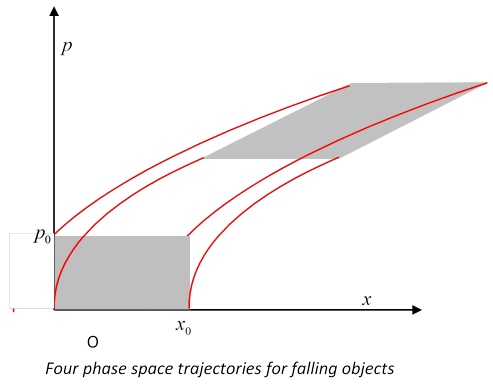
Here’s an example from Taylor of paths in phase space: four identical falling bodies are released simultaneously, see figure, x measures distance vertically down. Two are released with zero momentum from the origin O and from a point \(\begin{equation}
x_{0}
\end{equation}\) meters down, the other two are released with initial momenta \(\begin{equation}
p_{0}
\end{equation}\) again from the points O, \(\begin{equation}
x_{0}
\end{equation}\)

(Note the difference in initial slope.)

Check: convince yourself that all these paths are parts of parabolas centered on the x -axis. (Just as the simple harmonic oscillator phase space is filled with circular paths, this one is filled with parabolas.)

Bodies released with the same initial velocity at the same time will keep the same vertical distance apart, those released with different initial velocities will keep the same velocity difference, since all accelerate at g. Therefore, the area of the parallelogram formed by the four phase space points at a later time will have the same area as the initial square.

Exercise: convince yourself that all the points of an initial vertical side of the square all stay in line as time goes on, even though the line does not stay vertical.

The four sides of the square deform with time to the four sides of the parallelogram, point by point. This means that if we have a falling stone corresponding initially to a point inside the square, it will go to a point inside the parallelogram, because if somehow its path reached the boundary, we would have two paths in phase space intersecting, and a particle at one point in phase space has a uniquely defined future path (and past).