11.6: Jacobians 101

Suppose we are integrating a function over some region of ordinary three-dimensional space,

\[I=\int_{V} f\left(x_{1}, x_{2}, x_{3}\right) d x_{1} d x_{2} d x_{3}\]

but we want to change variables of integration to a different set of coordinates \(\left(q_{1}, q_{2}, q_{3}\right)\) such as, for example, \(\begin{equation}(r, \theta, \phi)\end{equation}\). The new coordinates are of course functions of the original ones \(\begin{equation}q_{1}\left(x_{1}, x_{2}, x_{3}\right)
\end{equation}\) etc., and we assume that in the region of integration they are smooth, well-behaved functions. We can’t simply re-express f  in terms of the new variables, and replace the volume differential \(\begin{equation}d x_{1} d x_{2} d x_{3} \text { by } d q_{1} d q_{2} d q_{3}\end{equation}\) that gives the wrong answer—in a plane, you can’t replace \(dxdy\) with \(drd\theta\), you have to use \(r\,dr\,d\theta\). That extra factor \(r\) is called the Jacobian, it’s clear that in the plane a small element with sides of fixed lengths \(\begin{equation}(\delta r, \delta \theta)\end{equation}\) is bigger the further it is from the origin, not all \(\begin{equation}\delta r \delta \theta\end{equation}\) elements are equal, so to speak. Our task is to construct the Jacobian for a general change of coordinates.

We need to think carefully about the volumes in the three-dimensional space represented by \(d x_{1} d x_{2} d x_{3}\) and by \(d q_{1} d q_{2} d q_{3}\). Of course, the \(x_{i}\)’s are just ordinary perpendicular Cartesian axes so the volume is just the product of the three sides of the little box, \(d x_{1} d x_{2} d x_{3}\).Imagine this little box, its corner closest to the origin at \(\left(x_{1}, x_{2}, x_{3}\right)\) and its furthest point at the other end of the body diagonal at \(\left(x_{1}+d x_{1}, x_{2}+d x_{2}, x_{3}+d x_{3}\right)\) Let’s take these two points in the qi coordinates to be at \(\left(q_{1}, q_{2}, q_{3}\right) \text { and }\left(q_{1}+d q_{1}, q_{2}+d q_{2}, q_{3}+d q_{3}\right)\). In visualizing this, bear in mind that the q axes need not be perpendicular to each other (but they cannot all lie in a plane, that would not be well-behaved).

For the \(x\) coordinate integration, we imagine filling the space with little cubical boxes. For the \(q\) integration, we have a system of space filling infinitesimal parallelepipeds, in general pointing different ways in different regions (think \((r, \theta)\). What we need to find is the volume of the incremental parallelepiped with sides we’ll write as vectors in x -coordinates, \(d \vec{q}_{1}, d \vec{q}_{2}, d \vec{q}_{3}\). These three incremental vectors are along the corresponding \(q\) coordinate axes, and the three added together are the displacement from \(\left(x_{1}, x_{2}, x_{3}\right) \text { to }\)

\[\left(x_{1}+d x_{1}, x_{2}+d x_{2}, x_{3}+d x_{3}\right) \equiv\left(q_{1}+d q_{1}, q_{2}+d q_{2}, q_{3}+d q_{3}\right)\]

Hence, in components,

\[d \vec{q}_{1}=\left(\dfrac{\partial q_{1}}{\partial x_{1}} d x_{1}, \dfrac{\partial q_{1}}{\partial x_{2}} d x_{2}, \dfrac{\partial q_{1}}{\partial x_{3}} d x_{3}\right)\]

Now the volume of the parallelepiped with sides the three vectors from the origin \(\vec{a}, \vec{b}, \vec{c} \text { is } \vec{a} \cdot \vec{b} \times \vec{c} \text { (recall }|\vec{b} \times \vec{c}| \text { is the }\) area of the parallelogram, then the dot product singles out the component of \(\vec{a}\) perpendicular to the plane of \(\vec{b}, \vec{c}\)).

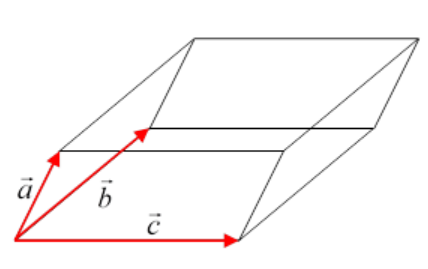
So, the volume corresponding to the increments \(d q_{1}, d q_{2}, d q_{3}\) in \(q\) space is

\[d \vec{q}_{1} \cdot d \vec{q}_{2} \times d \vec{q}_{3}=\left|\begin{array}{lll}
\dfrac{\partial q_{1}}{\partial x_{1}} & \dfrac{\partial q_{1}}{\partial x_{2}} & \dfrac{\partial q_{1}}{\partial x_{3}} \\
\dfrac{\partial q_{2}}{\partial x_{1}} & \dfrac{\partial q_{2}}{\partial x_{2}} & \dfrac{\partial q_{2}}{\partial x_{3}} \\
\dfrac{\partial q_{3}}{\partial x_{1}} & \dfrac{\partial q_{3}}{\partial x_{2}} & \dfrac{\partial q_{3}}{\partial x_{3}}
\end{array}\right| d x_{1} d x_{2} d x_{3}=\operatorname{Ddx}_{1} d x_{2} d x_{3}\]

writing \(D\) (Landau’s notation) for the determinant, which is in fact the Jacobian, often denoted by \(J\).

The standard notation for this determinantal Jacobian is

\[D=\dfrac{\partial\left(q_{1}, q_{2}, q_{3}\right)}{\partial\left(x_{1}, x_{2}, x_{3}\right)}\]

So the appropriate replacement for the three dimensional incremental volume element represented in the integral by \(d q_{1} d q_{2} d q_{3}\) is

\[d q_{1} d q_{2} d q_{3} \rightarrow \dfrac{\partial\left(q_{1}, q_{2}, q_{3}\right)}{\partial\left(x_{1}, x_{2}, x_{3}\right)} d x_{1} d x_{2} d x_{3}\]

The inverse

\[D^{-1}=\dfrac{\partial\left(x_{1}, x_{2}, x_{3}\right)}{\partial\left(q_{1}, q_{2}, q_{3}\right)}\]

is easily established using the chain rule for differentiation.

Exercise \(\PageIndex{1}\)

check this!

Thus the change of variables in an integral is accomplished by rewriting the integrand in the new variables, and replacing

\[I=\int_{V} f\left(x_{1}, x_{2}, x_{3}\right) d x_{1} d x_{2} d x_{3}=\int_{V} f\left(q_{1}, q_{2}, q_{3}\right) \dfrac{\partial\left(x_{1}, x_{2}, x_{3}\right)}{\partial\left(q_{1}, q_{2}, q_{3}\right)} d q_{1} d q_{2} d q_{3}\]

The argument in higher dimensions is just the same: on going to dimension \(n + 1\), the hypervolume element is equal to that of the \(n\) dimensional element multiplied by the component of the new vector perpendicular to the \(n\) dimensional element. The determinantal form does this automatically, since a determinant with two identical rows is zero, so in adding a new vector only the component perpendicular to all the earlier vectors contributes.

We’ve seen that the chain rule for differentiation gives the inverse as just the Jacobian with numerator and denominator reversed, it also readily yields

\[\dfrac{\partial\left(x_{1}, x_{2}, x_{3}\right)}{\partial\left(q_{1}, q_{2}, q_{3}\right)} \cdot \dfrac{\partial\left(q_{1}, q_{2}, q_{3}\right)}{\partial\left(r_{1}, r_{2}, r_{3}\right)}=\dfrac{\partial\left(x_{1}, x_{2}, x_{3}\right)}{\partial\left(r_{1}, r_{2}, r_{3}\right)}\]

and this extends trivially to n dimensions.

It’s also evident form the determinantal form of the Jacobian that

\[\dfrac{\partial\left(x_{1}, x_{2}, x_{3}\right)}{\partial\left(q_{1}, q_{2}, x_{3}\right)}=\dfrac{\partial\left(x_{1}, x_{2}\right)}{\partial\left(q_{1}, q_{2}\right)}\]

identical variables in numerator and denominator can be canceled. Again, this extends easily to \(n\) dimensions.