11.8: Simpler Proof of Liouville’s Theorem

Last updated
Save as PDF

Page ID: 30253

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Landau’s proof given above is extremely elegant: since phase space paths cannot intersect, point inside a volume stay inside, no matter how the volume contorts, and since time development is a canonical transformation, the total volume, given by integrating over volume elements \(dqdp\), stays the same, since it’s an integral over the corresponding volume elements \(dQdP\) and we’ve just shown that \(dQdP=dqdp\).

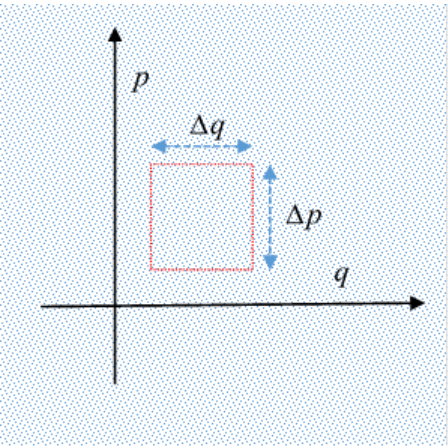
Here we’ll take a slightly different point of view: we’ll look at a small square in phase space and track how its edges are moving, to prove its volume isn’t changing. (We’ll stick to one dimension, but the generalization is straightforward.)

The points here represent a “gas” of many systems in the two dimensional \((q,p)\) phase space, and with a small square area \(\Delta q, \Delta p\) tagged by having all the systems on its boundary represented by dots of a different color. What is the incremental change in area of this initially square piece of phase space in time \(dt\)?

Begin with the top edge: the particles are all moving with velocities \((\dot{q}, \dot{p})\) but of course the only change in area comes from the \(\dot{p}\) term, that’s the outward movement of the boundary, so the area change in \(dt\) from the movement of this boundary will be \(\dot{p} \Delta q d t\). Meanwhile, there will be a similar term from the bottom edge, and the net contribution, top plus bottom edges, will depend on the change in \(\dot{p}\) from bottom to top, that is, a net area change from movement of these edges \((\partial \dot{p} / \partial p) \Delta p \Delta q d t\).

Adding in the other two edges (the sides), with an exactly similar argument, the total area change is

(\partial \dot{p} / \partial p+\partial \dot{q} / \partial q) \Delta p \Delta q d t

But from Hamilton’s equations \(\dot{p}=\partial H / \partial q, \quad \dot{q}=-\partial H / \partial p, \text { so }\)

\(\partial \dot{p} / \partial p=\partial^{2} H / \partial p \partial q, \quad \partial \dot{q} / \partial q=-\partial^{2} H / \partial p \partial q\)

and therefore

\(\partial \dot{p} / \partial p+\partial \dot{q} / \partial q=0\)

establishing that the total incremental area change as the square distorts is zero.

The conclusion is that the flow of the gas of systems in phase space is like an incompressible fluid, but with one important qualification: the density may vary with position! It just doesn’t vary along a dynamical path.