The Mach-Zehnder Interferometer

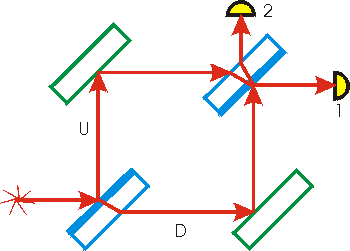The Mach-Zehnder interferometer, invented over one hundred years ago, is still used for many optical measurements. The "Mach" is the same man who proposed Mach's Principle and for whom a unit for the measurement of the speed of sound is named. Here we describe the details of how a simple version of the interferometer works; the discussion is largely non-mathematical but somewhat lengthy. A figure of the interferometer appears to the right.

The "legend" for the figure is:

Light source:		Mirror:
Detector:		Half-silvered mirror:

It turns out that, despite the figure, all of the light from the source ends up at detector 1; no light gets to detector 2. We will prove that this is so.

First, we will need to know the following facts from optics

• The "half-silvered" mirror is just a crummy mirror: it only reflects half the light incident on it, refracting the other half through it. Such mirrors are sometimes called one way glass. Sometimes we shall call it a beam splitter.
• The speed of light in air is almost the speed of light c in a vacuum. In terms of the index of refraction n=c/v ,where v is the speed of light in the medium, the index of refraction of air is almost exactly 1.
• The speed of light in glass is significantly less than c. For most glasses, the index of refraction is on the order of 1.5 or so. Put another way, the speed of light in glass is on the order of two-thirds of the speed of light in a vacuum.
• When a light ray is incident on a surface and the material on the other side of the surface has a higher index of refraction (i.e. a lower speed of light than the medium that the light is traveling in), then the reflected light ray is shifted in its phase by exactly one half a wavelength.
• The index of refraction of a perfect mirror can be thought of as infinite. Thus light reflected by a mirror has its phase changed by one half a wavelength.
• When a light ray is incident on a surface and the material on the other side of the surface has a lower index of refraction, the reflected light ray does not have its phase changed.
• When a light ray goes from one medium into another, its direction changes due to refraction but no phase change occurs at the surfaces of the two mediums.
• When a light ray travels through a medium, such as a glass plate, its phase will be shifted by an amount that depends on the index of refraction of the medium and the path length of the light ray through the medium.

Note we have labeled the two detectors 1 and 2, and have labeled the upper path of the light U and the down path of the light D. We consider the two paths for light arriving at detector 1:

Path "U":

1. Reflected by the front of the first beam splitter, giving a phase change of one-half a wavelength.
2. Reflected by the upper-left mirror, giving a further phase change of one-half a wavelength.
3. Transmitted through the upper-right beam splitter, giving some constant phase change.

Path "D":

1. Transmitted through the lower-left beam splitter, giving some constant phase change.
2. Reflected by the front of the lower-right mirror, giving a phase change of one-half a wavelength.
3. Reflected by the front of the second beam splitter, giving a phase change of one-half a wavelength.

Adding up all the contributions for the two paths, we see that they are the same. Thus light entering detector 1 via the two paths is in phase. Thus we get constructive interference for the light entering detector 1.

Now we consider light entering detector 2:

Path "U":

1. Reflected by the front of the first beam splitter, giving a phase change of one-half a wavelength.
2. Reflected by the upper-left mirror, giving a further phase change of one-half a wavelength.
3. Transmitted through the second beam splitter, giving some constant phase change.
4. Reflected by the inner surface of the second beam splitter, giving no phase change.
5. Transmitted through the beam splitter a second time, giving an additional constant phase change.

Path "D":

1. Transmitted through the lower-left beam splitter, giving some constant phase change.
2. Reflected by the front of the lower-right mirror, giving a phase change of one-half a wavelength.
3. Transmitted through the second beam splitter, giving some constant phase change.

Adding up all these, we see that the total difference between the two paths is that the U path has gone through one additional phase change of one-half a wavelength. Therefore, there will be complete destructive interference, and no light will reach detector 2.

Thus we have proved that, regardless of the wavelength of the light, it all goes to detector 1.

The interferometer is used to measure the phase shift of a thin sample of, say, glass. The sample is placed in either the U or D beam. The phase shift of the sample alters the phase relationships between the two beams that we have just described, and there is no longer complete destructive interference at detector 2. Measuring the relative amount of light entering detector 1 and detector 2 allows a calculation of the phase shift produced by the sample.