Waves and Wave Motion
- Page ID
- 3396
General.
1. Waves come in a variety of types:
Longitudinal or Transverse ; Periodic or Aperiodic ; Traveling or Standing
In this course we will deal mainly with traveling, periodic, transverse waves.
2. For Periodic waves, we can define:
A : the amplitude (the maximum oscillation, measured from the "zero" position).
\(\lambda \): the wavelength (the distance in which the wave repeats itself)
f : the frequency (the number of oscillations in one second)
V : the speed (the length of the wave passing a given point in one second)
I : the intensity of the wave (the amount of energy it carries).
Periodic waves come in many shapes and sizes - square, sinusoidal, sawtooth, to name but a few.
3. Due to these definitions, there is a relationship between wavelength, frequency and speed;
Speed = wavelength times frequency ( or \(V = \lambda f\))
4. Since the speed of a wave in a given medium is constant, dependent on the elastic constants (at a given temperature, pressure, etc.) of the medium, this means that a wave with a low value of frequency has a long wavelength, and vice-versa.
5. One of the most important features of waves arises because of the Superposition Principle which states that the total effect of any number of waves at a point is due to a simple algebraic sum (i.e. the sign of the oscillation at that point has to be taken into account) of the individual contributions from each wave arriving at that point. Due to this principle, waves exhibit interference - examples are the double slit experiment, diffraction of waves; also standing waves can be thought of as the sum of two traveling waves going in opposite directions.
This means that waves can interfere with each other. An example is given in Figure I : here the waves lie exactly on top of each other and are said to be in phase - as a result their waves and troughs add up to provide an example of constructive interference. In Figure II however, the waves and troughs cancel each other out : the waves are said to be out of phase, and in this case they exhibit destructive interference so that their sum is zero.
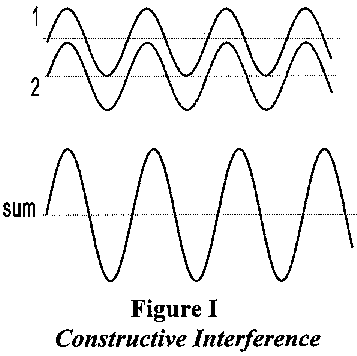
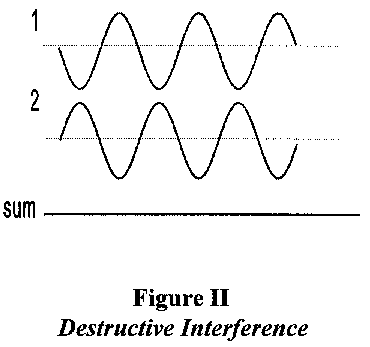
The ability to interfere in this manner is an important signature of waves.
6. The Intensity, I, of a wave is proportional to the square of its amplitude; I = A2 .
7. When a wave encounters a physical object (e.g. an aperture in a barrier, or a small obstacle in the path of the wave) its effect depends on the relative size of the object d and the wavelength of the wave. (e.g. when a wave passes through an aperture in a barrier, the diffraction, or spreading out of the wave will be greater for small apertures). Specifically, note that if the wavelength is much smaller than \(d ( \lambda \ll d )\), wavelike behavior (interference) will not be noticed. If however the wavelength approaches d, interference effects will begin to be observed. In fact, this effect sets the limit on the resolution of optical instruments; for example, if two small objects are closer together than a distance which is about the size of the wavelength used to observe them, the interference effects make it hard or impossible to distinguish between them.
THE NATURE OF LIGHT - the classical view.
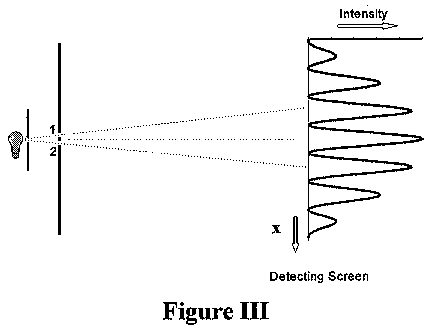
Isaac Newton suggested that light, in view of its ability to travel in straight lines and form sharp shadows round opaque objects, was corpuscular in nature. This hypothesis, supported by Newton's authority and the lack of any contrary evidence, held sway till the 19th century when improved measurements allowed the observation of what appeared to be wave-like properties. The most famous of these experiments was that of Thomas Young. Young illuminated a pair of closely spaced slits in an opaque screen with a monochromatic beam of light (light containing only one color). On another screen, placed at some distance away from the first, on the other side of the light source, he observed interference fringes which are the unmistakable sign of a wave process (see Figure III).
Assuming that light was a wave, the simple classical theory of waves could be used to give a complete description of the intensity distribution of the interference pattern. The calculation of where the the maxima and minima of this pattern should occur is so simple that it is worth repeating here.
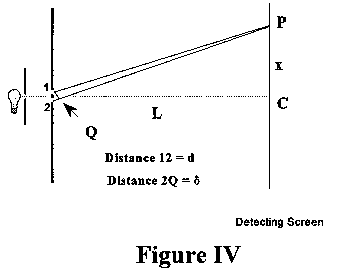
The argument is quite simple. Imagine that you were situated exactly at the center of the detecting screen shown in Figure IV. If you were to look back at the double slit system, the distance the two rays from each slit would have to travel exactly the same distance to reach you. They would thus arrive exactly in phase, and would add constructively. If now you were to move a little to the side of the center of the detecting screen, one ray would have to travel a slightly longer distance than the other to reach you. If the two distances from the slits differed by exactly one half wavelength, the two light waves would arrive exactly out of phase and would destructively interfere, so that you saw no light at that position on the screen. As you moved further away from the center of the screen, the two rays would successively pass into and out of phase, and you would see maxima and minima in the intensity pattern.
The Mathematics of the Interference of Light (optional!)
Assume that the wavelength of the light is \(\lambda\) , the spacing between the slits in the first screen is d, and the perpendicular distance between the two screens is L, as shown in Figure III. For convenience the two slits are labelled as 1 and 2. Consider an arbitrary point, P, on the detecting screen. Only if P were at the exact center of the detecting screen would the length of the light rays from slit 1 be exactly the same as the length of the light ray arriving at P from slit 2. In the general case, the lengths of these two light rays will be different. Consider the case shown in Figure IV where the length of the ray from slit 1 (call it 1) is less than the length of the ray coming from slit 2 (call it 2). If, then, the difference between these two lengths (2 -1) is an exact number of wavelengths, the effect of the two rays will add up - we say that they interfere constructively - and we would expect a maximum of the light intensity. On the other hand, if the difference in lengths (2 -1) is an odd number of half wavelengths, the two rays will cancel, or interfere destructively, and we expect a minimum (zero) of light intensity reaching the point P. At other places, where (2 -1) lies between these two values, we would expect intermediate values of intensity.
If we call the distance (2 -1) = e, we can express these conditions succintly (where n is an integer, 0,1,2,3,....) : if e = n\(\lambda\) , there will be a maximum at P: if e = {(2n +1) /2}\(\lambda\) = (n + 1/2)\(\lambda\) , there will be a minimum at P. Thus the central maximum will occur when e = 0 (at the center of the detecting screen), the first zero at e = \(\lambda\)/2, the next maximum at e =\(\lambda\) , the next zero at e = 3 \(\lambda\)/2, and so on. Now, in Figure II, let us draw in a perpendicular line from slit 1 to the light ray from slit 2 to P; let this line meet the line 2P in Q as shown. If the detecting screen is sufficiently far away from the double slits, to a very good approximation triangles 1CP, 2CP, and 1Q2, are similar (i.e. they have the same shape). Therefore the ratios PC/L = 2Q/d ; but PC is just x, the distance from the center of the detecting screen to the point P, and the distance 2Q is just the distance we have defined above as e. Thus x = Le/d. But the different values of e give us the positions of the zeroes and maxima of the interference pattern observed on the detecting screen. Thus, for example, the first zero is at x1 = Le/d = L\(\lambda\)/2d ; and the next zero is at x2 = Le/d = 3L\(\lambda\) /2d (substituting the values of e given above). So we can predict exactly where the maxima and minima of the interference pattern will occur, if we know the value of the wavelength of the light we are using.
Alternatively, knowing the dimensions of our apparatus, we can calculate the wavelength of the light. For example, the distance between the first two zeroes is given by (x2 - x1) = 3L /2d - L /2d = L /d. So, knowing the values of the distances involved, we can calculate the wavelength. It turns out that the wavelength of visible light is in the range of 4x10-7 (violet) to 7.5x10-7 (red) meters. In a similar, and almost as simple a fashion, the magnitude of the intensity of light at each point on the detecting screen can be calculated; that this simple assumption that light is a wave can yield such an accurate description of observation goes a long way to assuring us that we are on the right track.

