Prologue
- Page ID
- 9697
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two dramatically different philosophical approaches to science were developed in the field of classical mechanics during the 17\(^{th}\) - 18\(^{th}\) centuries. This time period coincided with the Age of Enlightenment in Europe during which remarkable intellectual and philosophical developments occurred. This was a time when both philosophical and causal arguments were equally acceptable in science, in contrast with current convention where there appears to be tacit agreement to discourage use of philosophical arguments in science.
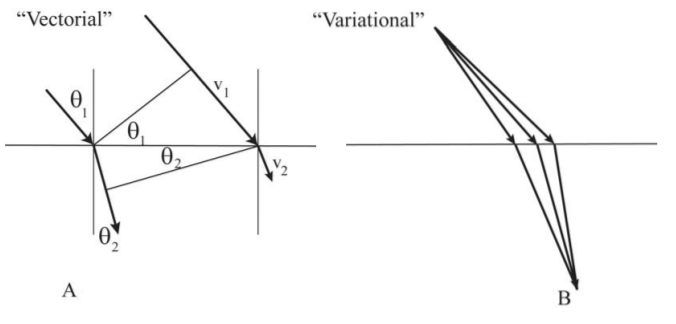
Figure \(\PageIndex{1}\): Vectorial and variational representation of Snell’s Law for refraction of light.
Snell's Law
The genesis of two contrasting philosophical approaches to science relates back to early studies of the reflection and refraction of light. The velocity of light in a medium of refractive index \(\textit{n}\) equals \(\mathit{v = \frac{c}{n} }\). Thus a light beam incident at an angle \( \theta_1 \) to the normal of a plane interface between medium 1 and medium 2 is refracted at an angle \( \theta_2 \) in medium 2 where the angles are related by Snell’s Law.
\[\label{eq:Snell's Law}\tag{Snell's Law}
\frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1} \]
Ibn Sahl of Bagdad (984) first described the refraction of light, while Snell (1621) derived his law mathematically. Both of these scientists used the "vectorial approach" where the light velocity \( \mathit{v} \) is considered to be a vector pointing in the direction of propagation.
Fermat's Principle
Fermat’s principle of least time (1657), which is based on the work of Hero of Alexandria (~ 60) and Ibn al-Haytham (1021), states that "light travels between two given points along the path of shortest time," where the transit time \( \tau \) of a light beam between two locations \(\mathit{A}\) and \(\mathit{B}\) in a medium with position-dependent refractive index \(\mathit{n(s)}\) given by
\[\tag{Fermat's Principle}
\tau= \int_{t_A}^{t_B}dt = \frac{1}{c} \int_A^Bn(s)ds
\label{eq:Fermat's Principle} \]
Fermat’s Principle leads to the derivation of Snell’s Law.
Philosophically the physics underlying the contrasting vectorial and Fermat’s Principle derivations of Snell’s Law are dramatically different. The vectorial approach is based on differential relations between the velocity vectors in the two media, whereas Fermat’s variational approach is based on the fact that the light preferentially selects a path for which the integral of the transit time between the initial location \(A\) and the final location \(B\) is minimized. That is, the first approach is based on “vectorial mechanics” whereas Fermat’s approach is based on variational principles in that the path between the initial and final locations is varied to find the path that minimizes the transit time. Fermat’s enunciation of variational principles in physics played a key role in the historical development, and subsequent exploitation, of the principle of least action in analytical formulations of classical mechanics as discussed below.
Newtonian Mechanics
Momentum and force are vectors that underlie the Newtonian formulation of classical mechanics. Newton’s monumental treatise, entitled “Philosophiae Naturalis Principia Mathematica”, published in 1687, established his three universal laws of motion, the universal theory of gravitation, the derivation of Kepler’s three laws of planetary motion, and the development of calculus. Newton’s three universal laws of motion provide the most intuitive approach to classical mechanics in that they are based on vector quantities like momentum, and the rate of change of momentum, which are related to force. Newton’s equation of motion
\[{\bf F} = \frac{d{\bf p}}{dt} \tag{Newton’s equation of motion}\]
is a vector differential relation between the instantaneous forces and rate of change of momentum, or equivalent instantaneous acceleration, all of which are vector quantities. Momentum and force are easy to visualize, and both cause and effect are embedded in Newtonian mechanics. Thus, if all of the forces, including the constraint forces, acting on the system are known, then the motion is solvable for two body systems. The mathematics for handling Newton’s “vectorial mechanics” approach to classical mechanics is well established.
Analytical Mechanics
Variational principles apply to many aspects of our daily life. Typical examples include; selecting the optimum compromise in quality and cost when shopping, selecting the fastest route to travel from home to work, or selecting the optimum compromise to satisfy the disparate desires of the individuals comprising a family. Variational principles underlie the analytical formulation of mechanics. It is astonishing that the laws of nature are consistent with variational principles involving the principle of least action. Minimizing the action integral led to the development of the mathematical field of variational calculus, plus the analytical variational approaches to classical mechanics, by Euler, Lagrange, Hamilton, and Jacobi.
Leibniz, who was a contemporary of Newton, introduced methods based on a quantity called “vis viva”, which is Latin for “living force” and equals twice the kinetic energy. Leibniz believed in the philosophy that God created a perfect world where nature would be thrifty in all its manifestations. In 1707, Leibniz proposed that the optimum path is based on minimizing the time integral of the vis viva, which is equivalent to the action integral of Lagrangian/Hamiltonian mechanics. In 1744 Euler derived the Leibniz result using variational concepts while Maupertuis restated the Leibniz result based on teleological arguments. The development of Lagrangian mechanics culminated in the 1788 publication of Lagrange’s monumental treatise entitled “Mécanique Analytique”. Lagrange used d’Alembert’s Principle to derive Lagrangian mechanics providing a powerful analytical approach to determine the magnitude and direction of the optimum trajectories, plus the associated forces.
The culmination of the development of analytical mechanics occurred in 1834 when Hamilton proposed his Principle of Least Action, as well as developing Hamiltonian mechanics which is the premier variational approach in science. Hamilton’s concept of least action is defined to be the time integral of the Lagrangian. Hamilton’s Action Principle (1834) minimizes the action integral \(S\) defined by
\[S = \int^B_A L({\bf q}, {\bf \dot{q}}, t ) dt \tag{Hamilton’s Principle}\]
In the simplest form, the Lagrangian \(L({\bf q}, {\bf \dot{q}}, t )\) equals the difference between the kinetic energy \(T\) and the potential energy \(U\). Hamilton’s Least Action Principle underlies Lagrangian mechanics. This Lagrangian is a function of \(n\) generalized coordinates \(q_i\) plus their corresponding velocities \(\dot{q}_i\). Hamilton also developed the premier variational approach, called Hamiltonian mechanics, that is based on the Hamiltonian \(H({\bf q}, {\bf p}, t)\) which is a function of the \(n\) fundamental position \(q_i\) plus the conjugate momentum \(p_i\) variables. In 1843 Jacobi provided the mathematical framework required to fully exploit the power of Hamiltonian mechanics. Note that the Lagrangian, Hamiltonian, and the action integral, all are scalar quantities which simplifies derivation of the equations of motion compared with the vector calculus used by Newtonian mechanics.
Figure \(\PageIndex{2}\) presents a philosophical roadmap illustrating the hierarchy of philosophical approaches based on Hamilton’s Action Principle, that are available for deriving the equations of motion of a system. The primary \({\bf Stage1}\) uses Hamilton’s Action functional, \(S = \int^{t_f}_{t_i} L ({\bf q}, {\bf \dot{q}}, t) dt\) to derive the Lagrangian, and Hamiltonian functionals which provide the most fundamental and sophisticated level of understanding. \({\bf Stage1}\) involves specifying all the active degrees of freedom, as well as the interactions involved. \({\bf Stage2}\) uses the Lagrangian or Hamiltonian functionals, derived at \({\bf Stage1}\), in order to derive the equations of motion for the system of interest. \({\bf Stage3}\) then uses these derived equations of motion to solve for the motion of the system subject to a given set of initial boundary conditions. Note that Lagrange first derived Lagrangian mechanics based on d’ Alembert’s Principle, while Newton’s Laws of Motion specify the equations of motion used in Newtonian mechanics.
The analytical approach to classical mechanics appeared contradictory to Newton’s intuitive vectorial treatment of force and momentum. There is a dramatic difference in philosophy between the vector-differential equations of motion derived by Newtonian mechanics, which relate the instantaneous force to the corresponding instantaneous acceleration, and analytical mechanics, where minimizing the scalar action integral involves integrals over space and time between specified initial and final states. Analytical mechanics uses variational principles to determine the optimum trajectory, from a continuum of tentative possibilities, by requiring that the optimum trajectory minimizes the action integral between specified initial and final conditions.
Initially there was considerable prejudice and philosophical opposition to use of the variational principles approach which is based on the assumption that nature follows the principles of economy. The variational approach is not intuitive, and thus it was considered to be speculative and “metaphysical”, but it was tolerated as an efficient tool for exploiting classical mechanics. This opposition to the variational principles underlying analytical mechanics, delayed full appreciation of the variational approach until the start of the 20\(^{th}\) century. As a consequence, the intuitive Newtonian formulation reigned supreme in classical mechanics for over two centuries, even though the remarkable problem-solving capabilities of analytical mechanics were recognized and exploited following the development of analytical mechanics by Lagrange.
The full significance and superiority of the analytical variational formulations of classical mechanics became well recognised and accepted following the development of the Special Theory of Relativity in 1905. The Theory of Relativity requires that the laws of nature be invariant to the reference frame. This is not satisfied by the Newtonian formulation of mechanics which assumes one absolute frame of reference and a separation of space and time. In contrast, the Lagrangian and Hamiltonian formulations of the principle of least action remain valid in the Theory of Relativity, if the Lagrangian is written in a relativistically-invariant form in space-time. The complete invariance of the variational approach to coordinate frames is precisely the formalism necessary for handling relativistic mechanics.
Hamiltonian mechanics, which is expressed in terms of the conjugate variables \((\mathbf{q}, \mathbf{p})\), relates classical mechanics directly to the underlying physics of quantum mechanics and quantum field theory. As a consequence, the philosophical opposition to exploiting variational principles no longer exists, and Hamiltonian mechanics has become the preeminent formulation of modern physics. The reader is free to draw their own conclusions regarding the philosophical question “is the principle of economy a fundamental law of classical mechanics, or is it a fortuitous consequence of the fundamental laws of nature?”
From the late seventeenth century, until the dawn of modern physics at the start of the twentieth century, classical mechanics remained a primary driving force in the development of physics. Classical mechanics embraces an unusually broad range of topics spanning motion of macroscopic astronomical bodies to microscopic particles in nuclear and particle physics, at velocities ranging from zero to near the velocity of light, from one-body to statistical many-body systems, as well as having extensions to quantum mechanics. Introduction of the Special Theory of Relativity in 1905, and the General Theory of Relativity in 1916, necessitated modifications to classical mechanics for relativistic velocities, and can be considered to be an extended theory of classical mechanics. Since the 1920's, quantal physics has superseded classical mechanics in the microscopic domain. Although quantum physics has played the leading role in the development of physics during much of the past century, classical mechanics still is a vibrant field of physics that recently has led to exciting developments associated with non-linear systems and chaos theory. This has spawned new branches of physics and mathematics as well as changing our notion of causality.
Goals
The primary goal of this book is to introduce the reader to the powerful variational-principles approaches that play such a pivotal role in classical mechanics and many other branches of modern science and engineering. This book emphasizes the intellectual beauty of these remarkable developments, as well as stressing the philosophical implications that have had a tremendous impact on modern science. A secondary goal is to apply variational principles to solve advanced applications in classical mechanics in order to introduce many sophisticated and powerful mathematical techniques that underlie much of modern physics.
This book starts with a review of Newtonian mechanics plus the solutions of the corresponding equations of motion. This is followed by an introduction to Lagrangian mechanics, based on d’Alembert’s Principle, in order to develop familiarity in applying variational principles to classical mechanics. This leads to introduction of the more fundamental Hamilton’s Action Principle, plus Hamiltonian mechanics, to illustrate the power provided by exploiting the full hierarchy of stages available for applying variational principles to classical mechanics. Finally the book illustrates how variational principles in classical mechanics were exploited during the development of both relativisitic mechanics and quantum physics. The connections and applications of classical mechanics to modern physics, are emphasized throughout the book in an effort to span the chasm that divides the Newtonian vector-differential formulation, and the integral variational formulation, of classical mechanics. This chasm is especially applicable to quantum mechanics which is based completely on variational principles. Note that variational principles, developed in the field of classical mechanics, now are used in a diverse and wide range of fields outside of physics, including economics, meteorology, engineering, and computing.
This study of classical mechanics involves climbing a vast mountain of knowledge, and the pathway to the top leads to elegant and beautiful theories that underlie much of modern physics. This book exploits variational principles applied to four major topics in classical mechanics to illustrate the power and importance of variational principles in physics. Being so close to the summit provides the opportunity to take a few extra steps beyond the normal introductory classical mechanics syllabus to glimpse the exciting physics found at the summit. This new physics includes topics such as quantum, relativistic, and statistical mechanics.


