4.7: Further Applications of Newton’s Laws of Motion
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Apply problem-solving techniques to solve for quantities in more complex systems of forces.
- Integrate concepts from kinematics to solve problems using Newton’s laws of motion.
There are many interesting applications of Newton’s laws of motion, a few more of which are presented in this section. These serve also to illustrate some further subtleties of physics and to help build problem-solving skills.
Example 4.7.1: Drag Force on a Barge
Suppose two tugboats push on a barge at different angles, as shown in Figure. The first tugboat exerts a force of 2.7×105N in the x-direction, and the second tugboat exerts a force of 3.6×105N in the y-direction.
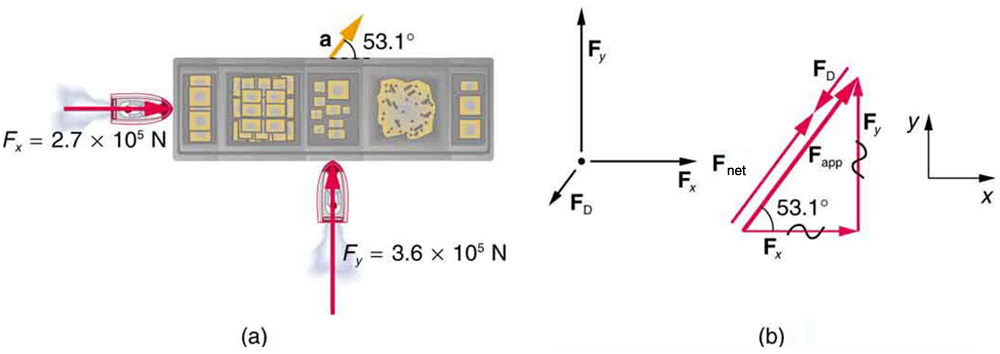
If the mass of the barge is 5.0×106 kg and its acceleration is observed to be 7.5×10−2m/s2 in the direction shown, what is the drag force of the water on the barge resisting the motion? (Note: drag force is a frictional force exerted by fluids, such as air or water. The drag force opposes the motion of the object.)
Strategy
The directions and magnitudes of acceleration and the applied forces are given in Figure (a). We will define the total force of the tugboats on the barge as Fapp so that:Fapp=Fx+Fy
Since the barge is flat bottomed, the drag of the water FD will be in the direction opposite to Fapp as shown in the free-body diagram in Figure (b). The system of interest here is the barge, since the forces on it are given as well as its acceleration. Our strategy is to find the magnitude and direction of the net applied force Fapp, and then apply Newton’s second law to solve for the drag force FD.
Solution
Since Fx and Fy are perpendicular, the magnitude and direction of Fapp are easily found. First, the resultant magnitude is given by the Pythagorean theorem:
Fapp=√F2x+F2y
Fapp=√(2.7×105N)2+(3.6×105N)2=4.5×105N.
The angle is given by θ=tan−1(FyFx)
θ=tan−1(3.6×105N2.7×105N)=53o,
which we know, because of Newton’s first law, is the same direction as the acceleration. FD is in the opposite direction of Fapp, since it acts to slow down the acceleration. Therefore, the net external force is in the same direction as Fapp, but its magnitude is slightly less than Fapp. The problem is now one-dimensional. From Figure (b) we can see that
Fnet=Fapp−FD.
Thus, Fapp−FD=ma
This can be solved for the magnitude of the drag force of the water FD in terms of known quantities: FD=Fapp−ma
The direction of FD has already been determined to be in the direction opposite to Fapp or at an angle of 53o south of west.
Discussion
The numbers used in this example are reasonable for a moderately large barge. It is certainly difficult to obtain larger accelerations with tugboats, and small speeds are desirable to avoid running the barge into the docks. Drag is relatively small for a well-designed hull at low speeds, consistent with the answer to this example, where FD is less than 1/600th of the weight of the ship.
In the earlier example of a tightrope walker we noted that the tensions in wires supporting a mass were equal only because the angles on either side were equal. Consider the following example, where the angles are not equal; slightly more trigonometry is involved.
Example 4.7.2: Different Tensions at Different Angles
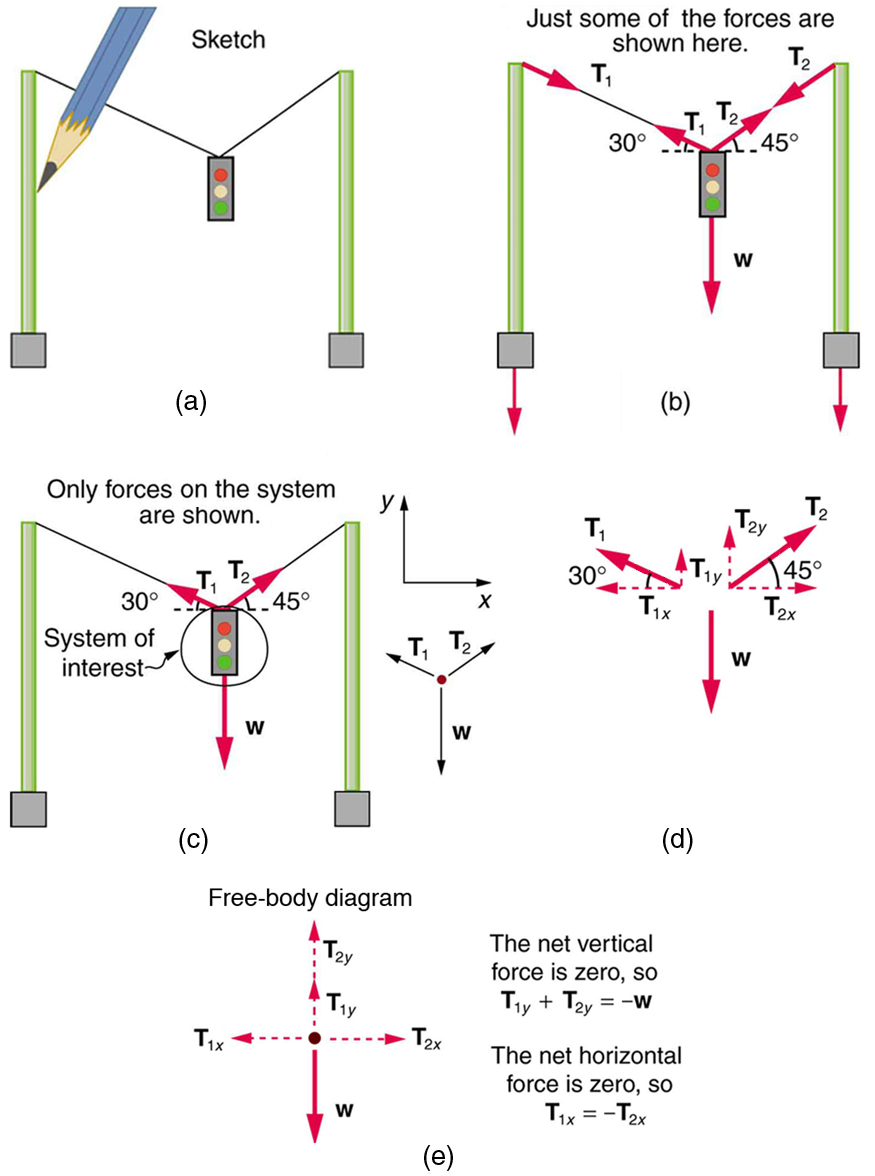
Consider the traffic light (mass 15.0 kg) suspended from two wires as shown in Figure. Find the tension in each wire, neglecting the masses of the wires.
Strategy
The system of interest is the traffic light, and its free-body diagram is shown in Figure(c). The three forces involved are not parallel, and so they must be projected onto a coordinate system. The most convenient coordinate system has one axis vertical and one horizontal, and the vector projections on it are shown in part (d) of the figure. There are two unknowns in this problem (T1 and T_2\)), so two equations are needed to find them. These two equations come from applying Newton’s second law along the vertical and horizontal axes, noting that the net external force is zero along each axis because acceleration is zero.
Solution
First consider the horizontal or x-axis: Fnetx=T2x−T1x=0.
Thus, as you might expect, T1x=T2x
This gives us the following relationship between T1 and T2: T1cos30o=T2cos 45o
Thus, T2=(1.225)T1.
Note that T1 and T2 are not equal in this case, because the angles on either side are not equal. It is reasonable that T2 ends up being greater than T1, because it is exerted more vertically than T1.
Now consider the force components along the vertical or y-axis:
Fnety=T1y+T2y−w=0
This implies T1y+T2y=w
Substituting the expressions for the vertical components gives T1sin(30o)+T2sin(45o)=w.
There are two unknowns in this equation, but substituting the expression for T2 in terms of T1 reduces this to one equation with one unknown:
T1(0.500)+(1.225T1)(0.707)=w=mg
which yields (1.366)T1=(15.0kg)(9.80m/s2).
Solving this last equation gives the magnitude of T1 to be T1=108N.
Finally, the magnitude of T2 is determined using the relationship between them, T2=1.225T1 found above. Thus we obtain
T2=132N.
Discussion
Both tensions would be larger if both wires were more horizontal, and they will be equal if and only if the angles on either side are the same (as they were in the earlier example of a tightrope walker).
The bathroom scale is an excellent example of a normal force acting on a body. It provides a quantitative reading of how much it must push upward to support the weight of an object. But can you predict what you would see on the dial of a bathroom scale if you stood on it during an elevator ride? Will you see a value greater than your weight when the elevator starts up? What about when the elevator moves upward at a constant speed: will the scale still read more than your weight at rest? Consider the following example.
Example 4.7.3: What does the Bathroom Scale Read in an Elevator?
Figure shows a 75.0-kg man (weight of about 165 lb) standing on a bathroom scale in an elevator. Calculate the scale reading: (a) if the elevator accelerates upward at a rate of 1.20m/s2 and (b) if the elevator moves upward at a constant speed of 1 m/s.
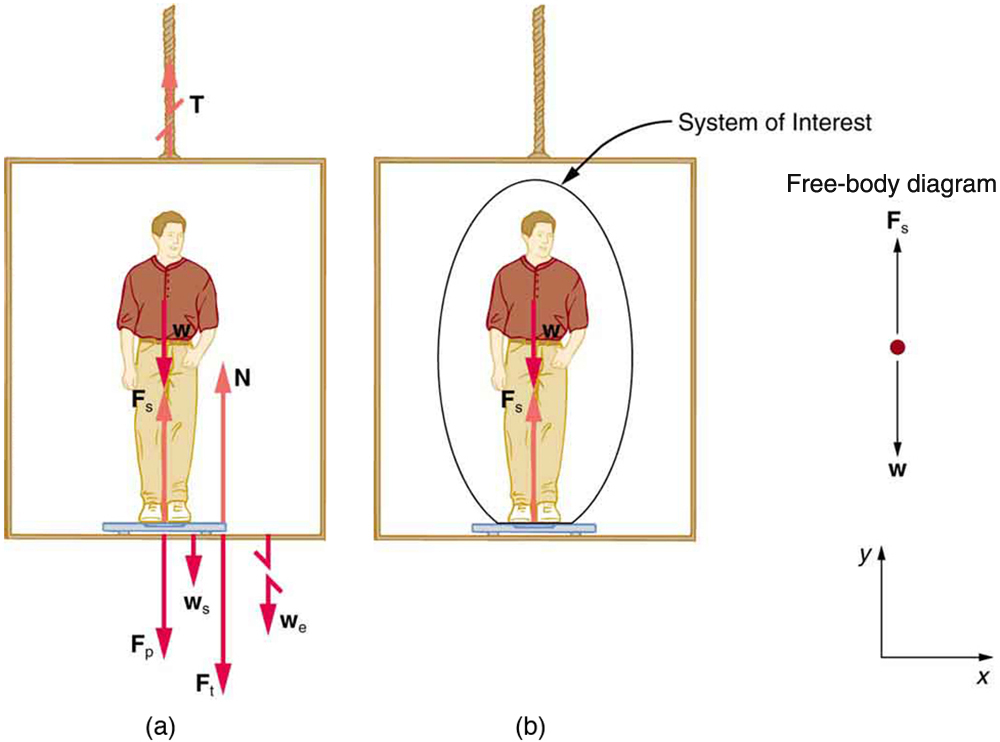
Strategy
If the scale is accurate, its reading will equal Fp the magnitude of the force the person exerts downward on it. Figure (a) shows the numerous forces acting on the elevator, scale, and person. It makes this one-dimensional problem look much more formidable than if the person is chosen to be the system of interest and a free-body diagram is drawn as in Figure (b). Analysis of the free-body diagram using Newton’s laws can produce answers to both parts (a) and (b) of this example, as well as some other questions that might arise. The only forces acting on the person are his weight w and the upward force of the scale Fs. According to Newton’s third law Fp and Fs are equal in magnitude and opposite in direction, so that we need to find Fs in order to find what the scale reads. We can do this, as usual, by applying Newton’s second law,
Fnet=ma
From the free-body diagram we see that Fnet=Fs−w, so that Fs−w=ma.
Solving for Fs gives an equation with only one unknown: Fs=ma+w,
or, because w=mg, simply Fs=ma+mg.
No assumptions were made about the acceleration, and so this solution should be valid for a variety of accelerations in addition to the ones in this exercise.
Solution for (a)
In this part of the problem, a=1.20m/s2, so that
Fs=(75.0kg)(1.20m/s2)+(75.0kg)(9.80m/s2),
yielding Fs=825N.
Discussion for (a)
This is about 185 lb. What would the scale have read if he were stationary? Since his acceleration would be zero, the force of the scale would be equal to his weight:
Fnet=ma=0=Fs−w
Fs=w=mg
Fs=(75.0kg)(9.80m/s2)
Fs=735N.
So, the scale reading in the elevator is greater than his 735-N (165 lb) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators.
Solution for (b)
Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more than his weight? For any constant velocity—up, down, or stationary—acceleration is zero because a=ΔvΔt and Δv=0.
Thus, Fs=ma+mg=0+mg.
Now Fs=(75.0kg)(9.80m/s2),
which gives Fs=735N.
Discussion for (b)
The scale reading is 735 N, which equals the person’s weight. This will be the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.
The solution to the previous example also applies to an elevator accelerating downward, as mentioned. When an elevator accelerates downward, a is negative, and the scale reading is less than the weight of the person, until a constant downward velocity is reached, at which time the scale reading again becomes equal to the person’s weight. If the elevator is in free-fall and accelerating downward at g, then the scale reading will be zero and the person will appear to be weightless.
Integrating Concepts: Newton’s Laws of Motion and Kinematics
Physics is most interesting and most powerful when applied to general situations that involve more than a narrow set of physical principles. Newton’s laws of motion can also be integrated with other concepts that have been discussed previously in this text to solve problems of motion. For example, forces produce accelerations, a topic of kinematics, and hence the relevance of earlier chapters. When approaching problems that involve various types of forces, acceleration, velocity, and/or position, use the following steps to approach the problem:
Problem-Solving Strategy
Step 1. Identify which physical principles are involved. Listing the givens and the quantities to be calculated will allow you to identify the principles involved.
Step 2. Solve the problem using strategies outlined in the text. If these are available for the specific topic, you should refer to them. You should also refer to the sections of the text that deal with a particular topic. The following worked example illustrates how these strategies are applied to an integrated concept problem.
Example 4.7.4: What Force Must a Soccer Player Exert to Reach Top Speed?
A soccer player starts from rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 s. (a) What was his average acceleration? (b) What average force did he exert backward on the ground to achieve this acceleration? The player’s mass is 70.0 kg, and air resistance is negligible.
Strategy
- To solve an integrated concept problem, we must first identify the physical principles involved and identify the chapters in which they are found. Part (a) of this example considers acceleration along a straight line. This is a topic of kinematics. Part (b) deals with force, a topic of dynamics found in this chapter.
- The following solutions to each part of the example illustrate how the specific problem-solving strategies are applied. These involve identifying knowns and unknowns, checking to see if the answer is reasonable, and so forth.
Solution for (a)
We are given the initial and final velocities (zero and 8.00 m/s forward); thus, the change in velocity is Δv=8.00m/s. We are given the elapsed time, and so Δt=2.50s. The unknown is acceleration, which can be found from its definition:
a=ΔvΔt.
Substituting the known values yields a=8.00m/s2.50s=3.20m/s2
Discussion for (a)
This is an attainable acceleration for an athlete in good condition.
Solution for (b)
Here we are asked to find the average force the player exerts backward to achieve this forward acceleration. Neglecting air resistance, this would be equal in magnitude to the net external force on the player, since this force causes his acceleration. Since we now know the player’s acceleration and are given his mass, we can use Newton’s second law to find the force exerted. That is,
Fnet=ma
Substituting the known values of m and a gives
Fnet=(70kg)(3.2m/s2)=224N.
Discussion for (b)
This is about 50 pounds, a reasonable average force.
This worked example illustrates how to apply problem-solving strategies to situations that include topics from different chapters. The first step is to identify the physical principles involved in the problem. The second step is to solve for the unknown using familiar problem-solving strategies. These strategies are found throughout the text, and many worked examples show how to use them for single topics. You will find these techniques for integrated concept problems useful in applications of physics outside of a physics course, such as in your profession, in other science disciplines, and in everyday life. The following problems will build your skills in the broad application of physical principles.
Summary
- Newton’s laws of motion can be applied in numerous situations to solve problems of motion.
- Some problems will contain multiple force vectors acting in different directions on an object. Be sure to draw diagrams, resolve all force vectors into horizontal and vertical components, and draw a free-body diagram. Always analyze the direction in which an object accelerates so that you can determine whether Fnet=ma or Fnet=0.
- The normal force on an object is not always equal in magnitude to the weight of the object. If an object is accelerating, the normal force will be less than or greater than the weight of the object. Also, if the object is on an inclined plane, the normal force will always be less than the full weight of the object.
- Some problems will contain various physical quantities, such as forces, acceleration, velocity, or position. You can apply concepts from kinematics and dynamics in order to solve these problems of motion.


