9.6: Forces and Torques in Muscles and Joints
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Explain the forces exerted by muscles.
- State how a bad posture causes back strain.
- Discuss the benefits of skeletal muscles attached close to joints.
- Discuss various complexities in the real system of muscles, bones, and joints.
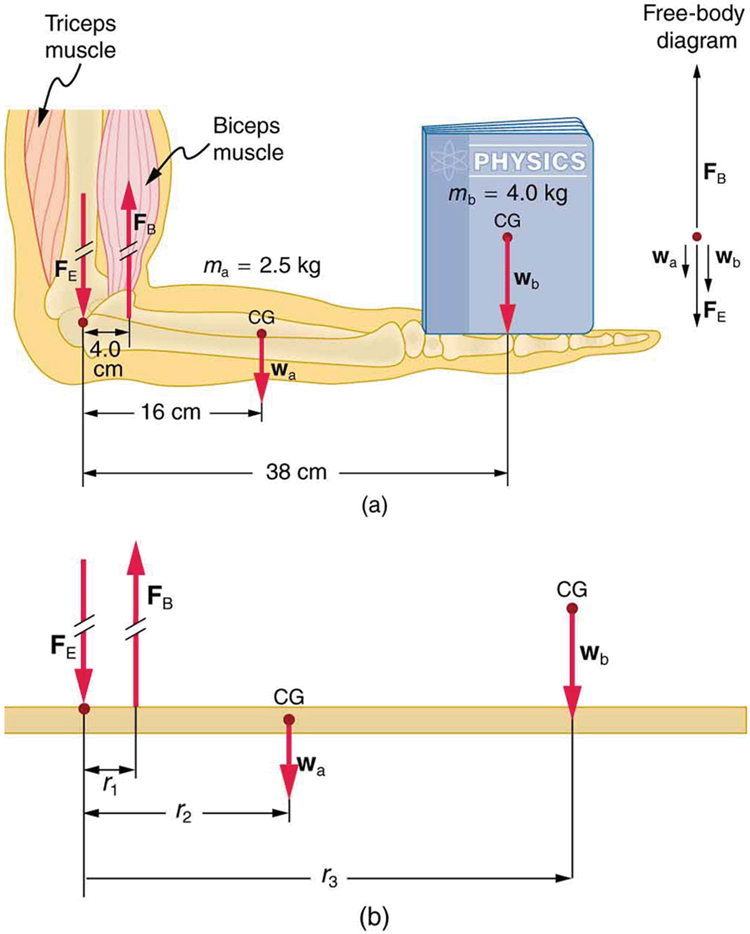
Muscles, bones, and joints are some of the most interesting applications of statics. There are some surprises. Muscles, for example, exert far greater forces than we might think. Figure shows a forearm holding a book and a schematic diagram of an analogous lever system. The schematic is a good approximation for the forearm, which looks more complicated than it is, and we can get some insight into the way typical muscle systems function by analyzing it.
Muscles can only contract, so they occur in pairs. In the arm, the biceps muscle is a flexor—that is, it closes the limb. The triceps muscle is an extensor that opens the limb. This configuration is typical of skeletal muscles, bones, and joints in humans and other vertebrates. Most skeletal muscles exert much larger forces within the body than the limbs apply to the outside world. The reason is clear once we realize that most muscles are attached to bones via tendons close to joints, causing these systems to have mechanical advantages much less than one. Viewing them as simple machines, the input force is much greater than the output force, as seen in Figure.
Example 9.6.1: Muscles Exert Bigger Forces Than You Might Think
Calculate the force the biceps muscle must exert to hold the forearm and its load as shown in Figure, and compare this force with the weight of the forearm plus its load. You may take the data in the figure to be accurate to three significant figures.
Strategy
There are four forces acting on the forearm and its load (the system of interest). The magnitude of the force of the biceps is FB; that of the elbow joint is FE; that of the weights of the forearm is wa, and its loadis wb. Two of these are unknown (FB and FE) so that the first condition for equilibrium cannot by itself yield FB. But if we use the second condition and choose the pivot to be at the elbow, then the torque due to FB is zero, and the only unknown becomes FB.
Solution
The torques created by the weights are clockwise relative to the pivot, while the torque created by the biceps is counterclockwise; thus, the second condition for equilibrium (netτ=0) becomes
r2wa+r3wb=r1FB.
Note that sinθ=1 for all forces, since θ=90o for all forces. This equation can easily be solved for FB in terms of known quantities, yielding FB=r2wa+r3wbr1.
Entering the known values gives
FB=(0.160m)(2.50kg)(9.80m/s2)+(0.380m)(4.00kg)(9.80m/s2)0.0400m
which yields FB=470N.
Now, the combined weight of the arm and its load is
(6.50kg)(9.80m/s2)=63.7N, so that the ratio of the force exerted by the biceps to the total weight is
FBwa+wb=47063.7=7.38.
Discussion
This means that the biceps muscle is exerting a force 7.38 times the weight supported.
In the above example of the biceps muscle, the angle between the forearm and upper arm is 90°. If this angle changes, the force exerted by the biceps muscle also changes. In addition, the length of the biceps muscle changes. The force the biceps muscle can exert depends upon its length; it is smaller when it is shorter than when it is stretched.
Very large forces are also created in the joints. In the previous example, the downward force FE exerted by the humerus at the elbow joint equals 407 N, or 6.38 times the total weight supported. (The calculation of FE is straightforward and is left as an end-of-chapter problem.) Because muscles can contract, but not expand beyond their resting length, joints and muscles often exert forces that act in opposite directions and thus subtract. (In the above example, the upward force of the muscle minus the downward force of the joint equals the weight supported—that is, 470N−470N=63N, approximately equal to the weight supported.) Forces in muscles and joints are largest when their load is a long distance from the joint, as the book is in the previous example.
In racquet sports such as tennis the constant extension of the arm during game play creates large forces in this way. The mass times the lever arm of a tennis racquet is an important factor, and many players use the heaviest racquet they can handle. It is no wonder that joint deterioration and damage to the tendons in the elbow, such as “tennis elbow,” can result from repetitive motion, undue torques, and possibly poor racquet selection in such sports. Various tried techniques for holding and using a racquet or bat or stick not only increases sporting prowess but can minimize fatigue and long-term damage to the body. For example, tennis balls correctly hit at the “sweet spot” on the racquet will result in little vibration or impact force being felt in the racquet and the body—less torque as explained in Collisions of Extended Bodies in Two Dimensions. Twisting the hand to provide top spin on the ball or using an extended rigid elbow in a backhand stroke can also aggravate the tendons in the elbow.
Training coaches and physical therapists use the knowledge of relationships between forces and torques in the treatment of muscles and joints. In physical therapy, an exercise routine can apply a particular force and torque which can, over a period of time, revive muscles and joints. Some exercises are designed to be carried out under water, because this requires greater forces to be exerted, further strengthening muscles. However, connecting tissues in the limbs, such as tendons and cartilage as well as joints are sometimes damaged by the large forces they carry. Often, this is due to accidents, but heavily muscled athletes, such as weightlifters, can tear muscles and connecting tissue through effort alone.
The back is considerably more complicated than the arm or leg, with various muscles and joints between vertebrae, all having mechanical advantages less than 1. Back muscles must, therefore, exert very large forces, which are borne by the spinal column. Discs crushed by mere exertion are very common. The jaw is somewhat exceptional—the masseter muscles that close the jaw have a mechanical advantage greater than 1 for the back teeth, allowing us to exert very large forces with them. A cause of stress headaches is persistent clenching of teeth where the sustained large force translates into fatigue in muscles around the skull.
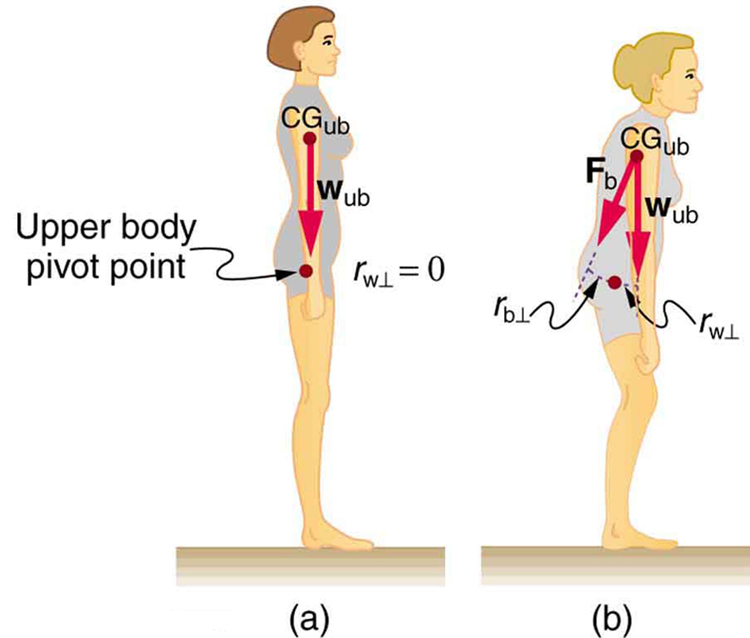
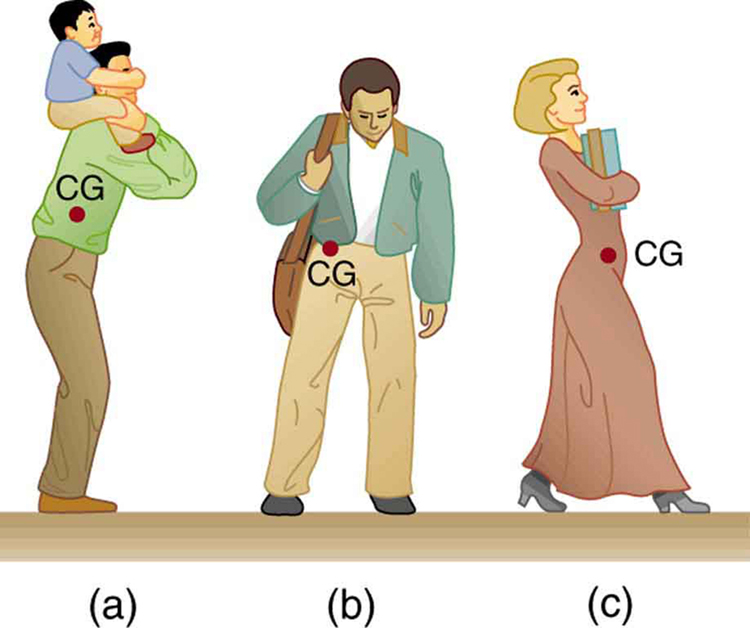
Figure shows how bad posture causes back strain. In part (a), we see a person with good posture. Note that her upper body’s cg is directly above the pivot point in the hips, which in turn is directly above the base of support at her feet. Because of this, her upper body’s weight exerts no torque about the hips. The only force needed is a vertical force at the hips equal to the weight supported. No muscle action is required, since the bones are rigid and transmit this force from the floor. This is a position of unstable equilibrium, but only small forces are needed to bring the upper body back to vertical if it is slightly displaced. Bad posture is shown in part (b); we see that the upper body’s cg is in front of the pivot in the hips. This creates a clockwise torque around the hips that is counteracted by muscles in the lower back. These muscles must exert large forces, since they have typically small mechanical advantages. (In other words, the perpendicular lever arm for the muscles is much smaller than for the cg.) Poor posture can also cause muscle strain for people sitting at their desks using computers. Special chairs are available that allow the body’s CG to be more easily situated above the seat, to reduce back pain. Prolonged muscle action produces muscle strain. Note that the cg of the entire body is still directly above the base of support in part (b) of Figure. This is compulsory; otherwise the person would not be in equilibrium. We lean forward for the same reason when carrying a load on our backs, to the side when carrying a load in one arm, and backward when carrying a load in front of us, as seen in Figure.
You have probably been warned against lifting objects with your back. This action, even more than bad posture, can cause muscle strain and damage discs and vertebrae, since abnormally large forces are created in the back muscles and spine.
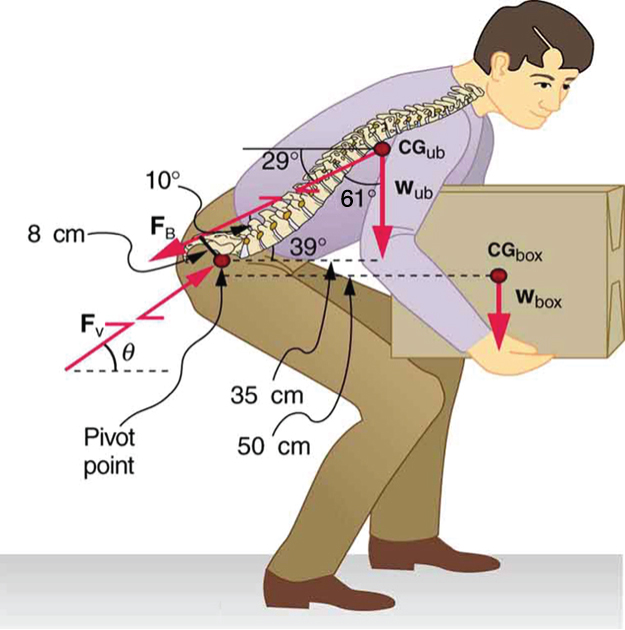
Example: 9.6.1: Do Not Lift with Your Back
Consider the person lifting a heavy box with his back, shown in Figure. (a) Calculate the magnitude of the force FB - in the back muscles that is needed to support the upper body plus the box and compare this with his weight. The mass of the upper body is 55.0 kg and the mass of the box is 30.0 kg. (b) Calculate the magnitude and direction of the force FV - exerted by the vertebrae on the spine at the indicated pivot point. Again, data in the figure may be taken to be accurate to three significant figures.
Strategy
By now, we sense that the second condition for equilibrium is a good place to start, and inspection of the known values confirms that it can be used to solve for FB - if the pivot is chosen to be at the hips. The torques created by wab and wbox - are clockwise, while that created by FB - is counterclockwise.
Solution for (a)
Using the perpendicular lever arms given in the figure, the second condition for equilibrium (netτ=0) becomes
(0.350m)(55.0kg)(9.80m/s2)+(0.500m)(30.0kg)(9.80m/s2)=(0.0800m)FB
The ratio of the force the back muscles exert to the weight of the upper body plus its load is
FBwub+wbox=4200N833N=5.04.
This force is considerably larger than it would be if the load were not present.
Solution for (b)
More important in terms of its damage potential is the force on the vertebrae FV The first condition for equilibrium (netF=0) can be used to find its magnitude and direction. Using y fo4r vertical and x for horizontal, the condition for the net external forces along those axes to be zero
netFy=0andnetFx=0
Starting with the vertical (y) components, this yields
FVy−wub−wbox−FBsin29o=0.
FVy=wub+wbox+FBsin29.0o
=833N+(4200N)sin29.0o
FVy=2.87×103N.
Similarly, for the horizontal (x) components,
FVx−FBcos29.0o=0
FVx=3.67×103N.
The magnitude of FV is given by the Pythagorean theorem:
FV=√F2Vx+F2VY=4.66×103N.
The direction of FV is
θ=tan−1(FVyFVx)=38.0o.
Note that the ratio of FV to the weight supported is \]\dfrac{F_V}{w_{ub} + w_{box}} = \dfrac{4660 \, N}{833 \, N} = 5.59.\]
Discussion
This force is about 5.6 times greater than it would be if the person were standing erect. The trouble with the back is not so much that the forces are large—because similar forces are created in our hips, knees, and ankles—but that our spines are relatively weak. Proper lifting, performed with the back erect and using the legs to raise the body and load, creates much smaller forces in the back—in this case, about 5.6 times smaller.
What are the benefits of having most skeletal muscles attached so close to joints? One advantage is speed because small muscle contractions can produce large movements of limbs in a short period of time. Other advantages are flexibility and agility, made possible by the large numbers of joints and the ranges over which they function. For example, it is difficult to imagine a system with biceps muscles attached at the wrist that would be capable of the broad range of movement we vertebrates possess.
There are some interesting complexities in real systems of muscles, bones, and joints. For instance, the pivot point in many joints changes location as the joint is flexed, so that the perpendicular lever arms and the mechanical advantage of the system change, too. Thus the force the biceps muscle must exert to hold up a book varies as the forearm is flexed. Similar mechanisms operate in the legs, which explain, for example, why there is less leg strain when a bicycle seat is set at the proper height. The methods employed in this section give a reasonable description of real systems provided enough is known about the dimensions of the system. There are many other interesting examples of force and torque in the body—a few of these are the subject of end-of-chapter problems.
Summary
- Statics plays an important part in understanding everyday strains in our muscles and bones.
- Many lever systems in the body have a mechanical advantage of significantly less than one, as many of our muscles are attached close to joints.
- Someone with good posture stands or sits in such a way that their center of gravity lies directly above the pivot point in their hips, thereby avoiding back strain and damage to disks.


