11.3: Pressure
- Page ID
- 1563
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Define pressure.
- Explain the relationship between pressure and force.
- Calculate force given pressure and area.
You have no doubt heard the word pressure being used in relation to blood (high or low blood pressure) and in relation to the weather (high- and low-pressure weather systems). These are only two of many examples of pressures in fluids.
Definition: Pressure
Pressure is defined as the force divided by the area perpendicular to the force over which the force is applied, or
\[P = \dfrac{F}{A}. \label{pressure}\]
where \(F\) is a force applied to an area \(A\) that is perpendicular to the force.
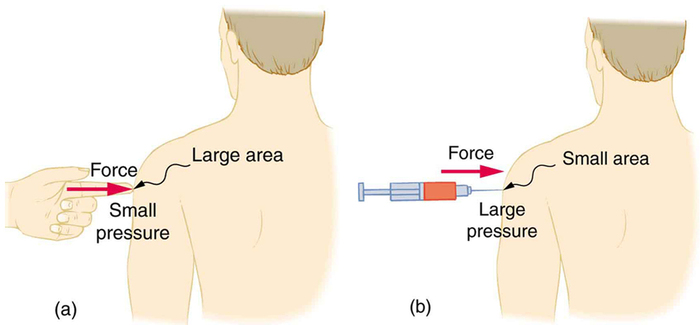
A given force can have a significantly different effect depending on the area over which the force is exerted, as shown in Figure Figure \(\PageIndex{1}\). The SI unit for pressure is the pascal, where
\[1 \, Pa = 1 \, N/m^2.\]
In addition to the pascal, there are many other units for pressure that are in common use. In meteorology, atmospheric pressure is often described in units of millibar (mb), where
\[100 \, mb = 1 \times 10^4 \, Pa.\]
Pounds per square inch \((lb/in^2 \, or \, psi)\) is still sometimes used as a measure of tire pressure, and millimeters of mercury (mm Hg) is still often used in the measurement of blood pressure. Pressure is defined for all states of matter but is particularly important when discussing fluids.
Example \(\PageIndex{1}\): Calculating Force Exerted by the Air - What Force Does a Pressure Exert?
An astronaut is working outside the International Space Station where the atmospheric pressure is essentially zero. The pressure gauge on her air tank reads \(6.9 \times 10^6 \, Pa\). What force does the air inside the tank exert on the flat end of the cylindrical tank, a disk 0.150 m in diameter?
Strategy
We can find the force exerted from the definition of pressure (Equation \red{pressure}) provided we can find the area \(A\) acted upon.
Solution
By rearranging the definition of pressure (Equation \red{pressure}) to solve for force, we see that
\[F = PA.\nonumber\]
Here, the pressure \(P\) is given, as is the area of the end of the cylinder \(A\), given by \(A = \pi r^2\). Thus
\[ \begin{align*} F &= (6.90 \times 10^6 \, Pa)(3.14)(0.0750 \, m)^2 \\[5pt] &= 1.22 \times 10^5 \, N. \end{align*}\]
Discussion
Wow! No wonder the tank must be strong. Since we found \(F = PA\), we see that the force exerted by a pressure is directly proportional to the area acted upon as well as the pressure itself.
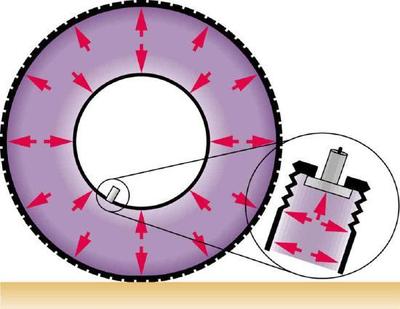
The force exerted on the end of the tank is perpendicular to its inside surface. This direction is because the force is exerted by a static or stationary fluid. We have already seen that fluids cannot withstand shearing (sideways) forces; they cannot exert shearing forces, either. Fluid pressure has no direction, being a scalar quantity. The forces due to pressure have well-defined directions: they are always exerted perpendicular to any surface. (See the tire in Figure \(\PageIndex{2}\), for example.)
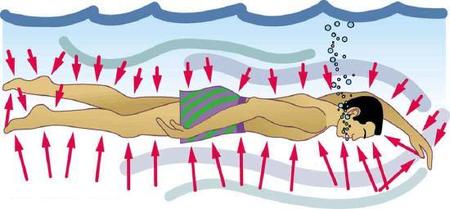
Finally, note that pressure is exerted on all surfaces. Swimmers, as well as the tire, feel pressure on all sides (Figure \(\PageIndex{3}\)).
PHET EXPLORATIONS: GAS PROPERTIES
Pump gas molecules in this simulation to a box and see what happens as you change the volume, add or remove heat, change gravity, and more. Measure the temperature and pressure, and discover how the properties of the gas vary in relation to each other.
Summary
- Pressure is the force per unit perpendicular area over which the force is applied. In equation form, pressure is defined as \[F = PA. \nonumber\]
- The SI unit of pressure is pascal and \(1 \, Pa = 1 \, N/m^2.\)
Glossary
- pressure
- the force per unit area perpendicular to the force, over which the force acts