19.1: Electric Potential Energy- Potential Difference
- Page ID
- 2650
Learning Objectives
By the end of this section, you will be able to:
- Define electric potential and electric potential energy.
- Describe the relationship between potential difference and electrical potential energy.
- Explain electron volt and its usage in submicroscopic process.
- Determine electric potential energy given potential difference and amount of charge.
When a free positive charge \(q\) is accelerated by an electric field, such as shown in Figure \(\PageIndex{1}\), it is given kinetic energy. The process is analogous to an object being accelerated by a gravitational field. It is as if the charge is going down an electrical hill where its electric potential energy is converted to kinetic energy. Let us explore the work done on a charge \(q\) by the electric field in this process, so that we may develop a definition of electric potential energy.
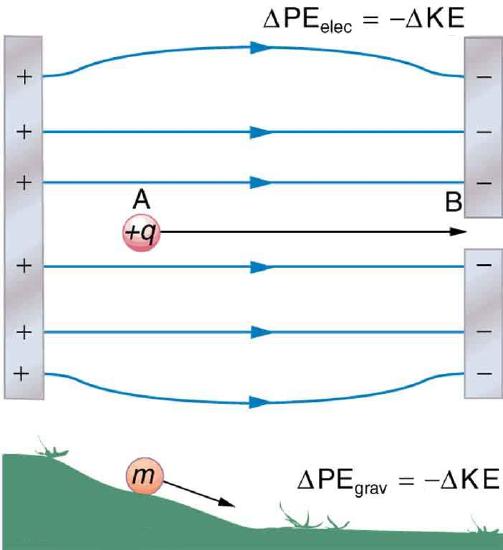
The electrostatic or Coulomb force is conservative, which means that the work done on \(q\) is independent of the path taken. This is exactly analogous to the gravitational force in the absence of dissipative forces such as friction. When a force is conservative, it is possible to define a potential energy associated with the force, and it is usually easier to deal with the potential energy (because it depends only on position) than to calculate the work directly.
We use the letters PE to denote electric potential energy, which has units of joules (J). The change in potential energy, \(\Delta \mathrm{PE}\), is crucial, since the work done by a conservative force is the negative of the change in potential energy; that is, \(W=-\Delta \mathrm{PE}\). For example, work \(W\) done to accelerate a positive charge from rest is positive and results from a loss in PE, or a negative \(\Delta \mathrm{PE}\). There must be a minus sign in front of \(\Delta \mathrm{PE}\) to make \(W\) positive. PE can be found at any point by taking one point as a reference and calculating the work needed to move a charge to the other point.
POTENTIAL ENERGY
\(W=-\Delta \mathrm{PE}\). For example, work \(W\) done to accelerate a positive charge from rest is positive and results from a loss in PE, or a negative \(\Delta \mathrm{PE}\) There must be a minus sign in front of \(\Delta \mathrm{PE}\) to make \(W\) positive. PE can be found at any point by taking one point as a reference and calculating the work needed to move a charge to the other point.
Gravitational potential energy and electric potential energy are quite analogous. Potential energy accounts for work done by a conservative force and gives added insight regarding energy and energy transformation without the necessity of dealing with the force directly. It is much more common, for example, to use the concept of voltage (related to electric potential energy) than to deal with the Coulomb force directly.
Calculating the work directly is generally difficult, since \(W=Fd\cos \theta\) and the direction and magnitude of \(F\) can be complex for multiple charges, for odd-shaped objects, and along arbitrary paths. But we do know that, since \(F=qE\), the work, and hence \(\Delta \mathrm{PE}\), is proportional to the test charge \(q\) To have a physical quantity that is independent of test charge, we define electric potential \(V\) (or simply potential, since electric is understood) to be the potential energy per unit charge:
\[V=\dfrac{\mathrm{PE}}{q}.\]
ELECTRIC POTENTIAL
This is the electric potential energy per unit charge.
\[V=\dfrac{\mathrm{PE}}{q}\]
Since PE is proportional to \(q\), the dependence on \(q\) cancels. Thus \(V\) does not depend on \(q\). The change in potential energy \(\Delta \mathrm{PE}\) is crucial, and so we are concerned with the difference in potential or potential difference \(\Delta V\) between two points, where
\[\Delta V =V_{B}-V_{A}=\dfrac{\Delta \mathrm{PE}}{q}.\]
The potential difference between points A and B, \(V_{B}-V_{A}\), is thus defined to be the change in potential energy of a charge \(q\) moved from A to B, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta.
\[1\mathrm{V}=1\mathrm{\dfrac{J}{C}}\]
POTENTIAL DIFFERENCE
The potential difference between points A and B, \(V_{B}-V_{A}\), is defined to be the change in potential energy of a charge \(q\) moved from A to B, divided by the charge. Units of potential difference are joules per coulomb, given the name volt (V) after Alessandro Volta.
\[1\mathrm{V}=1\mathrm{\dfrac{J}{C}}\]
The familiar term voltage is the common name for potential difference. Keep in mind that whenever a voltage is quoted, it is understood to be the potential difference between two points. For example, every battery has two terminals, and its voltage is the potential difference between them. More fundamentally, the point you choose to be zero volts is arbitrary. This is analogous to the fact that gravitational potential energy has an arbitrary zero, such as sea level or perhaps a lecture hall floor.
In summary, the relationship between potential difference (or voltage) and electrical potential energy is given by
\[\Delta V=\dfrac{\Delta \mathrm{PE}}{q}\: \mathrm{and}\: \Delta \mathrm{PE}=q\Delta V.\]
POTENTIAL DIFFERENCE AND ELECTRICAL POTENTIAL ENERGY
The relationship between potential difference (or voltage) and electrical potential energy is given by
\[\Delta =\dfrac{\Delta \mathrm{PE}}{q}\: \mathrm{and}\: \Delta \mathrm{PE}=q\Delta V.\]
The second equation is equivalent to the first.
Voltage is not the same as energy. Voltage is the energy per unit charge. Thus a motorcycle battery and a car battery can both have the same voltage (more precisely, the same potential difference between battery terminals), yet one stores much more energy than the other since \(\Delta PE=q\Delta V\). The car battery can move more charge than the motorcycle battery, although both are 12 V batteries.
Example \(\PageIndex{1}\):Calculating Energy
Suppose you have a 12.0 V motorcycle battery that can move 5000 C of charge, and a 12.0 V car battery that can move 60,000 C of charge. How much energy does each deliver? (Assume that the numerical value of each charge is accurate to three significant figures.)
Strategy
To say we have a 12.0 V battery means that its terminals have a 12.0 V potential difference. When such a battery moves charge, it puts the charge through a potential difference of 12.0 V, and the charge is given a change in potential energy equal to \(\Delta PE=q\Delta V\).
So to find the energy output, we multiply the charge moved by the potential difference.
Solution
For the motorcycle battery, \(q=5000 \mathrm{C}\) and \(\Delta =12.0\mathrm{V}\). The total energy delivered by the motorcycle battery is
\[\Delta \mathrm{PE}_{cycle}=(5000\mathrm{C})(12.0\mathrm{V})\]
\[=(5000\mathrm{C})(12.0\mathrm{J/C})\]
\[=6.00\times 10^{4}\mathrm{J}.\]
Similarly, for the car battery, \(q=60,000\mathrm{C}\) and
\[\Delta \mathrm{PE}_{car}=(60,000\mathrm{C})(12.0\mathrm{V})\]
\[=7.20\times 10^{5}\mathrm{J}.\]
Discussion
While voltage and energy are related, they are not the same thing. The voltages of the batteries are identical, but the energy supplied by each is quite different. Note also that as a battery is discharged, some of its energy is used internally and its terminal voltage drops, such as when headlights dim because of a low car battery. The energy supplied by the battery is still calculated as in this example, but not all of the energy is available for external use.
Note that the energies calculated in the previous example are absolute values. The change in potential energy for the battery is negative, since it loses energy. These batteries, like many electrical systems, actually move negative charge—electrons in particular. The batteries repel electrons from their negative terminals (A) through whatever circuitry is involved and attract them to their positive terminals (B) as shown in Figure \(\PageIndex{2}\). The change in potential is \(\Delta V =V_{B}-V_{A}=+12\mathrm{V}\) and the charge \(q\) is negative, so that \(\Delta \mathrm{PE}=q\Delta V\) is negative, meaning the potential energy of the battery has decreased when \(q\) has moved from A to B.
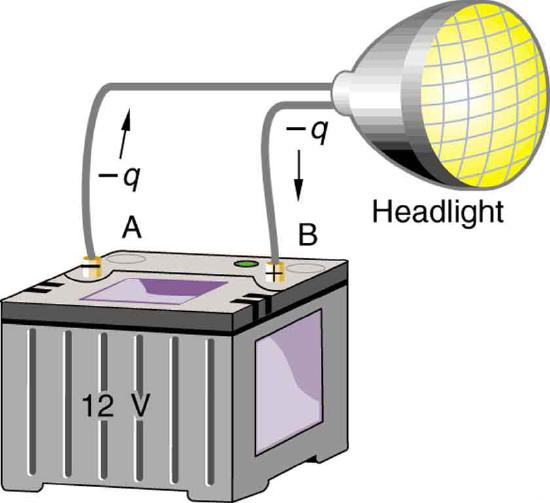
Example \(\PageIndex{2}\): How Many Electrons Move through a Headlight Each Second?
When a 12.0 V car battery runs a single 30.0 W headlight, how many electrons pass through it each second?
Strategy
To find the number of electrons, we must first find the charge that moved in 1.00 s. The charge moved is related to voltage and energy through the equation \(\Delta \mathrm{PE}=q\Delta V\). A 30.0 W lamp uses 30.0 joules per second. Since the battery loses energy, we have \(\Delta \mathrm{PE}=-30.0J\) and, since the electrons are going from the negative terminal to the positive, we see that \(\Delta V=+12.0V\).
Solution
To find the charge \(q\) moved, we solve the equation \(\Delta \mathrm{PE}=q\Delta V\):
\[q=\dfrac{\Delta \mathrm{PE}}{\Delta V}.\]
Entering the values for \(\Delta PE\) and \(\Delta V\), we get
\[q=\dfrac{-30.0\mathrm{J}}{+12.0\mathrm{V}}=\dfrac{-30.0\mathrm{J}}{+12.0\mathrm{J/C}}=-2.50\mathrm{C}.\]
The number of electrons \(n_{e}\) is the total charge divided by the charge per electron. That is,
\[n_{e}=\dfrac{-2.50\mathrm{C}}{-1.60\times 10^{-19}\mathrm{C/e^{-}}}=1.56\times 10^{19} \mathrm{electrons}.\]
Discussion
This is a very large number. It is no wonder that we do not ordinarily observe individual electrons with so many being present in ordinary systems. In fact, electricity had been in use for many decades before it was determined that the moving charges in many circumstances were negative. Positive charge moving in the opposite direction of negative charge often produces identical effects; this makes it difficult to determine which is moving or whether both are moving.
The Electron Volt
The energy per electron is very small in macroscopic situations like that in the previous example—a tiny fraction of a joule. But on a submicroscopic scale, such energy per particle (electron, proton, or ion) can be of great importance. For example, even a tiny fraction of a joule can be great enough for these particles to destroy organic molecules and harm living tissue. The particle may do its damage by direct collision, or it may create harmful x rays, which can also inflict damage. It is useful to have an energy unit related to submicroscopic effects. Figure \(\PageIndex{3}\) shows a situation related to the definition of such an energy unit. An electron is accelerated between two charged metal plates as it might be in an old-model television tube or oscilloscope. The electron is given kinetic energy that is later converted to another form—light in the television tube, for example. (Note that downhill for the electron is uphill for a positive charge.) Since energy is related to voltage by \(\Delta PE=q\Delta V\) we can think of the joule as a coulomb-volt.
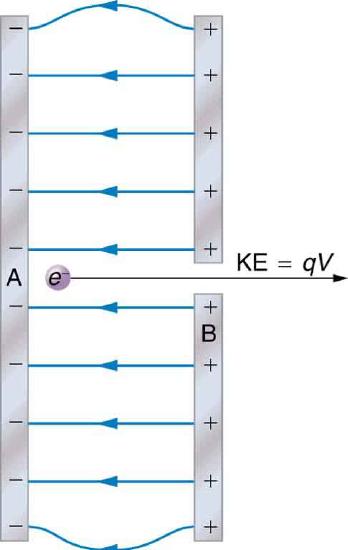
On the submicroscopic scale, it is more convenient to define an energy unit called the electron volt (eV), which is the energy given to a fundamental charge accelerated through a potential difference of 1 V. In equation form,
\[1\mathrm{ev}=(1.60\times 10^{-19}\mathrm{C})(1\mathrm{V})=(1.60\times 10^{-19}\mathrm{C})(1\mathrm{J/C})\]
\[=1.60\times 10^{-19}J.\]
ELECTRON VOLT
On the submicroscopic scale, it is more convenient to define an energy unit called the electron volt (eV), which is the energy given to a fundamental charge accelerated through a potential difference of 1 V. In equation form,
\[1 \mathrm{eV}=(1.60\times 10^{-19} \mathrm{C})(1 \mathrm{V})=(1.60\times 10^{-19} \mathrm{C}) (1\mathrm{J/C})\]
\[=1.60\times 10^{-19} \mathrm{C}\]
An electron accelerated through a potential difference of 1 V is given an energy of 1 eV. It follows that an electron accelerated through 50 V is given 50 eV. A potential difference of 100,000 V (100 kV) will give an electron an energy of 100,000 eV (100 keV), and so on. Similarly, an ion with a double positive charge accelerated through 100 V will be given 200 eV of energy. These simple relationships between accelerating voltage and particle charges make the electron volt a simple and convenient energy unit in such circumstances.
CONNECTIONS: ENERGY UNITS
The electron volt (eV) is the most common energy unit for submicroscopic processes. This will be particularly noticeable in the chapters on modern physics. Energy is so important to so many subjects that there is a tendency to define a special energy unit for each major topic. There are, for example, calories for food energy, kilowatt-hours for electrical energy, and therms for natural gas energy.
The electron volt is commonly employed in submicroscopic processes—chemical valence energies and molecular and nuclear binding energies are among the quantities often expressed in electron volts. For example, about 5 eV of energy is required to break up certain organic molecules. If a proton is accelerated from rest through a potential difference of 30 kV, it is given an energy of 30 keV (30,000 eV) and it can break up as many as 6000 of these molecules ( \(30,000 \mathrm{eV}\div 5\mathrm{eV}\) per molecule \(=6000\) molecules). Nuclear decay energies are on the order of 1 MeV (1,000,000 eV) per event and can, thus, produce significant biological damage.
Conservation of Energy
The total energy of a system is conserved if there is no net addition (or subtraction) of work or heat transfer. For conservative forces, such as the electrostatic force, conservation of energy states that mechanical energy is a constant.
Mechanical energy is the sum of the kinetic energy and potential energy of a system; that is, \(KE + PE=\: \mathrm{constant}\). A loss of PE of a charged particle becomes an increase in its KE. Here PE is the electric potential energy. Conservation of energy is stated in equation form as
\[\mathrm{KE}+\mathrm{PE}=\mathrm{constant}\]
or
\[\mathrm{KE}_{i}+\mathrm{PE}_{i}=\mathrm{KE}_{f}+\mathrm{PE}_{f},\]
where i and f stand for initial and final conditions. As we have found many times before, considering energy can give us insights and facilitate problem solving.
Example \(\PageIndex{3}\): Electrical Potential Energy Converted to Kinetic Energy
Calculate the final speed of a free electron accelerated from rest through a potential difference of 100 V. (Assume that this numerical value is accurate to three significant figures.)
Strategy
We have a system with only conservative forces. Assuming the electron is accelerated in a vacuum, and neglecting the gravitational force (we will check on this assumption later), all of the electrical potential energy is converted into kinetic energy. We can identify the initial and final forms of energy to be \(\mathrm{KE}_{i}=0,\mathrm{KE}_{f}=\dfrac{1}{2}mv^{2}, \mathrm{PE}_{i}=qV,\: \mathrm{and}\: \mathrm{PE}_{f}=0\).
Solution
Conservation of energy states that
\[\mathrm{KE}_{i}+\mathrm{PE}_{i}=\mathrm{KE}_{f}+\mathrm{PE}_{f}\]
Entering the forms identified above, we obtain
\[qV=\dfrac{mv^{2}}{2}.\]
We solve this for \(v\):
\[v=\sqrt {\dfrac{2qV}{m}}.\]
Entering values for \(q,\: V,\: \mathrm{and}\: m\) gives
\[v=\sqrt{\dfrac{2(-1.60\times 10^{-19}\mathrm{C})(-100 \mathrm{J/C})}{9.11\times 10^{-31}\mathrm{kg}}}\]
\[=5.93\times 10^{6} \mathrm{m/s}.\]
Discussion
Note that both the charge and the initial voltage are negative, as in Figure. From the discussions in Electric Charge and Electric Field, we know that electrostatic forces on small particles are generally very large compared with the gravitational force. The large final speed confirms that the gravitational force is indeed negligible here. The large speed also indicates how easy it is to accelerate electrons with small voltages because of their very small mass. Voltages much higher than the 100 V in this problem are typically used in electron guns. Those higher voltages produce electron speeds so great that relativistic effects must be taken into account. That is why a low voltage is considered (accurately) in this example.
Summary
- Electric potential is potential energy per unit charge.
- The potential difference between points A and B, \(V_{\mathrm{B}}-V_{\mathrm{A}}\), defined to be the change in potential energy of a charge \(q\) moved from A to B, is equal to the change in potential energy divided by the charge, Potential difference is commonly called voltage, represented by the symbol \(\Delta V\).
\(\Delta V= \dfrac{\Delta \mathrm{PE}}{q}\: \mathrm{and}\: \Delta \mathrm{PE}=q\Delta V.\)
- An electron volt is the energy given to a fundamental charge accelerated through a potential difference of 1 V. In equation form,
\(1\mathrm{eV}=(1.60\times 10^{-19}\mathrm{C})(1 \mathrm{V})=(1.60\times 10^{-19}\mathrm{C})(1 \mathrm{J/C})\)
\(=1.60\times 10^{-19}\mathrm{J}.\)
- Mechanical energy is the sum of the kinetic energy and potential energy of a system, that is, \(\mathrm{KE}+\mathrm{PE}\) This sum is a constant.
Glossary
- electric potential
- potential energy per unit charge
- potential difference (or voltage)
- change in potential energy of a charge moved from one point to another, divided by the charge; units of potential difference are joules per coulomb, known as volt
- electron volt
- the energy given to a fundamental charge accelerated through a potential difference of one volt
- mechanical energy
- sum of the kinetic energy and potential energy of a system; this sum is a constant


