30.E: Atomic Physics (Exercises)
- Last updated
- Save as PDF
- Page ID
- 9290
Conceptual Questions
30.1: Discovery of the Atom
1. Name three different types of evidence for the existence of atoms.
2. Explain why patterns observed in the periodic table of the elements are evidence for the existence of atoms, and why Brownian motion is a more direct type of evidence for their existence.
3. If atoms exist, why can’t we see them with visible light?
30.2: Discovery of the Parts of the Atom: Electrons and Nuclei
4. What two pieces of evidence allowed the first calculation of me, the mass of the electron? Justify your response.
(a) The ratios \(\displaystyle q_e/m_e\) and \(\displaystyle q_p/m_p\).
(b) The values of \(\displaystyle q_e\) and \(\displaystyle E_B\).
(c) The ratio \(\displaystyle q_e/m_e\) and \(\displaystyle q_e\).
5. How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around the sun? Explain how the correspondence principle applies here.
30.3: Bohr’s Theory of the Hydrogen Atom
6. How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around the sun? Explain how the correspondence principle applies here.
7. Explain how Bohr’s rule for the quantization of electron orbital angular momentum differs from the actual rule.
8. What is a hydrogen-like atom, and how are the energies and radii of its electron orbits related to those in hydrogen?
30.4: X Rays- Atomic Origins and Applications
9. Explain why characteristic x rays are the most energetic in the EM emission spectrum of a given element.
10. Why does the energy of characteristic x rays become increasingly greater for heavier atoms?
11. Observers at a safe distance from an atmospheric test of a nuclear bomb feel its heat but receive none of its copious x rays. Why is air opaque to x rays but transparent to infrared?
12. Lasers are used to burn and read CDs. Explain why a laser that emits blue light would be capable of burning and reading more information than one that emits infrared.
13. Crystal lattices can be examined with x rays but not UV. Why?
14. CT scanners do not detect details smaller than about 0.5 mm. Is this limitation due to the wavelength of x rays? Explain.
30.5: Applications of Atomic Excitations and De-Excitations
15. How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around the sun? Explain how the correspondence principle applies here.
16. Atomic and molecular spectra are discrete. What does discrete mean, and how are discrete spectra related to the quantization of energy and electron orbits in atoms and molecules?
17. Hydrogen gas can only absorb EM radiation that has an energy corresponding to a transition in the atom, just as it can only emit these discrete energies. When a spectrum is taken of the solar corona, in which a broad range of EM wavelengths are passed through very hot hydrogen gas, the absorption spectrum shows all the features of the emission spectrum. But when such EM radiation passes through room-temperature hydrogen gas, only the Lyman series is absorbed. Explain the difference.
18. Lasers are used to burn and read CDs. Explain why a laser that emits blue light would be capable of burning and reading more information than one that emits infrared.
19. The coating on the inside of fluorescent light tubes absorbs ultraviolet light and subsequently emits visible light. An inventor claims that he is able to do the reverse process. Is the inventor’s claim possible?
20. What is the difference between fluorescence and phosphorescence?
21. How can you tell that a hologram is a true three-dimensional image and that those in 3-D movies are not?
30.6: The Wave Nature of Matter Causes Quantization
22. How is the de Broglie wavelength of electrons related to the quantization of their orbits in atoms and molecules?
30.7: Patterns in Spectra Reveal More Quantization
23. What is the Zeeman effect, and what type of quantization was discovered because of this effect?
30.8: Quantum Numbers and Rules
24. Define the quantum numbers \(\displaystyle n, l,m_l, s\), and \(\displaystyle m_s\).
25. For a given value of \(\displaystyle n\), what are the allowed values of \(\displaystyle l\)?
26. For a given value of \(\displaystyle l\), what are the allowed values of \(\displaystyle m_l\)? What are the allowed values of \(\displaystyle m_l\) for a given value of \(\displaystyle n\)? Give an example in each case.
27. List all the possible values of \(\displaystyle s\) and \(\displaystyle m_s\) for an electron. Are there particles for which these values are different? The same?
30.9: The Pauli Exclusion Principle
28. Identify the shell, subshell, and number of electrons for the following:
(a) \(\displaystyle 2p^3\).
(b) \(\displaystyle 4d^9\).
(c) \(\displaystyle 3s^1\).
(d) \(\displaystyle 5g^{16}\).
29. Which of the following are not allowed? State which rule is violated for any that are not allowed.
(a) \(\displaystyle 1p^3\)
(b) \(\displaystyle 2p^8\)
(c) \(\displaystyle 3g^{11}\)
(d) \(\displaystyle 4f^2\)
Problems & Exercises
30.1: Discovery of the Atom
30. Using the given charge-to-mass ratios for electrons and protons, and knowing the magnitudes of their charges are equal, what is the ratio of the proton’s mass to the electron’s? (Note that since the charge-to-mass ratios are given to only three-digit accuracy, your answer may differ from the accepted ratio in the fourth digit.)
Solution
\(\displaystyle 1.84×10^3\)
31. (a) Calculate the mass of a proton using the charge-to-mass ratio given for it in this chapter and its known charge.
(b) How does your result compare with the proton mass given in this chapter?
32. If someone wanted to build a scale model of the atom with a nucleus 1.00 m in diameter, how far away would the nearest electron need to be?
Solution
50 km
30.2: Discovery of the Parts of the Atom: Electrons and Nuclei
33. Rutherford found the size of the nucleus to be about 10−15m. This implied a huge density. What would this density be for gold?
Solution
\(\displaystyle 6×10^{20}kg/m^3\)
34. In Millikan’s oil-drop experiment, one looks at a small oil drop held motionless between two plates. Take the voltage between the plates to be 2033 V, and the plate separation to be 2.00 cm. The oil drop (of density \(\displaystyle 0.81 g/cm^3\)) has a diameter of \(\displaystyle 4.0×10^{−6}m\). Find the charge on the drop, in terms of electron units.
35. (a) An aspiring physicist wants to build a scale model of a hydrogen atom for her science fair project. If the atom is 1.00 m in diameter, how big should she try to make the nucleus?
(b) How easy will this be to do?
Solution
(a) \(\displaystyle 10.0 μm\)
(b) It isn’t hard to make one of approximately this size. It would be harder to make it exactly 10.0 μm.
30.3: Bohr’s Theory of the Hydrogen Atom
36. By calculating its wavelength, show that the first line in the Lyman series is UV radiation.
Solution
\(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2_i})⇒λ=\frac{1}{R}[\frac{(n_i⋅n_f)^2}{n^2_i−n^2_f}];n_i=2,n_f=1,\) so that
\(\displaystyle λ=(\frac{m}{1.097×10^7})[\frac{(2×1)^2}{2^2−1^2}]=1.22×10^{−7}m=122 nm\) , which is UV radiation.
37. Find the wavelength of the third line in the Lyman series, and identify the type of EM radiation.
38. Look up the values of the quantities in \(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}\), and verify that the Bohr radius \(\displaystyle a_B\) is \(\displaystyle 0.529×10^{−10}m\).
Solution
\(\displaystyle a_B=\frac{h^2}{4π^2mekZq^2_e}=\frac{(6.626×10^{−34}J⋅s)^2}{4π^2(9.109×10^{−31}kg)(8.988×10^9N⋅m^2/C^2)(1)(1.602×10^{−19}C)^2}=0.529×10^{−10}m\)
39. Verify that the ground state energy \(\displaystyle E_0\) is 13.6 eV by using \(\displaystyle E0=\frac{2π^2q^4_em_ek^2}{h^2}\).
40. If a hydrogen atom has its electron in the \(\displaystyle n=4\) state, how much energy in eV is needed to ionize it?
Solution
0.850 eV
41. A hydrogen atom in an excited state can be ionized with less energy than when it is in its ground state. What is n for a hydrogen atom if 0.850 eV of energy can ionize it?
42. Find the radius of a hydrogen atom in the \(\displaystyle n=2\) state according to Bohr’s theory.
Solution
\(\displaystyle 2.12×10^{–10}m\)
43. Show that \(\displaystyle (13.6 eV)/hc=1.097×10^7m=R\) (Rydberg’s constant), as discussed in the text.
44. What is the smallest-wavelength line in the Balmer series? Is it in the visible part of the spectrum?
Solution
365 nm
It is in the ultraviolet.
45. Show that the entire Paschen series is in the infrared part of the spectrum. To do this, you only need to calculate the shortest wavelength in the series.
46. Do the Balmer and Lyman series overlap? To answer this, calculate the shortest-wavelength Balmer line and the longest-wavelength Lyman line.
Solution
No overlap
365 nm
122 nm
47. (a) Which line in the Balmer series is the first one in the UV part of the spectrum?
(b) How many Balmer series lines are in the visible part of the spectrum?
(c) How many are in the UV?
48. A wavelength of \(\displaystyle 4.653 μm\) is observed in a hydrogen spectrum for a transition that ends in the \(\displaystyle n_f=5\) level. What was \(\displaystyle n_i\) for the initial level of the electron?
Solution
7
49. A singly ionized helium ion has only one electron and is denoted \(\displaystyle He^+\). What is the ion’s radius in the ground state compared to the Bohr radius of hydrogen atom?
50. A beryllium ion with a single electron (denoted \(\displaystyle Be^{3+}\)) is in an excited state with radius the same as that of the ground state of hydrogen.
(a) What is \(\displaystyle n\) for the \(\displaystyle Be^{3+}\) ion?
(b) How much energy in eV is needed to ionize the ion from this excited state?
Solution
(a) 2
(b) 54.4 eV
51. Atoms can be ionized by thermal collisions, such as at the high temperatures found in the solar corona. One such ion is \(\displaystyle C^{+5}\), a carbon atom with only a single electron.
(a) By what factor are the energies of its hydrogen-like levels greater than those of hydrogen?
(b) What is the wavelength of the first line in this ion’s Paschen series?
(c) What type of EM radiation is this?
52. Verify Equations \(\displaystyle r_n=\frac{n^2}{Z}a_B\) and \(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}=0.529×10^{−10}m\) using the approach stated in the text. That is, equate the Coulomb and centripetal forces and then insert an expression for velocity from the condition for angular momentum quantization.
Solution
\(\displaystyle \frac{kZq^2_e}{r^2_n}=\frac{m_eV^2}{r_n}\), so that \(\displaystyle r_n=\frac{kZq^2_e}{m_eV^2}=\frac{kZq^2_e}{m_e}\frac{1}{V^2}\). From the equation \(\displaystyle m_evr_n=n\frac{h}{2π}\), we can substitute for the velocity, giving: \(\displaystyle r_n=\frac{kZq^2_e}{m_e}⋅\frac{4π^2m^2_er^2_n}{n^2h^2}\) so that \(\displaystyle r_n=\frac{n^2}{Z}\frac{h^2}{4π^2m_ekq^2_e}=\frac{n^2}{Z}a_B\), where \(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}\).
53. The wavelength of the four Balmer series lines for hydrogen are found to be 410.3, 434.2, 486.3, and 656.5 nm. What average percentage difference is found between these wavelength numbers and those predicted by \(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2+i})\)? It is amazing how well a simple formula (disconnected originally from theory) could duplicate this phenomenon.
30.4: X Rays- Atomic Origins and Applications
54. (a) What is the shortest-wavelength x-ray radiation that can be generated in an x-ray tube with an applied voltage of 50.0 kV?
(b) Calculate the photon energy in eV.
(c) Explain the relationship of the photon energy to the applied voltage.
Solution
(a) \(\displaystyle 0.248×10^{−10}m\)
(b) 50.0 keV
(c) The photon energy is simply the applied voltage times the electron charge, so the value of the voltage in volts is the same as the value of the energy in electron volts.
55. A color television tube also generates some x rays when its electron beam strikes the screen. What is the shortest wavelength of these x rays, if a 30.0-kV potential is used to accelerate the electrons? (Note that TVs have shielding to prevent these x rays from exposing viewers.)
56. An x ray tube has an applied voltage of 100 kV.
(a) What is the most energetic x-ray photon it can produce? Express your answer in electron volts and joules.
(b) Find the wavelength of such an X–ray.
Solution
(a) \(\displaystyle 100×10^3eV, 1.60×10^{−14}J\)
(b) \(\displaystyle 0.124×10^{−10}m\)
57. The maximum characteristic x-ray photon energy comes from the capture of a free electron into a \(\displaystyle K\) shell vacancy. What is this photon energy in keV for tungsten, assuming the free electron has no initial kinetic energy?
58. What are the approximate energies of the \(\displaystyle K_α\) and \(\displaystyle K_β\) x rays for copper?
Solution
(a) 8.00 keV
(b) 9.48 keV
30.5: Applications of Atomic Excitations and De-Excitations
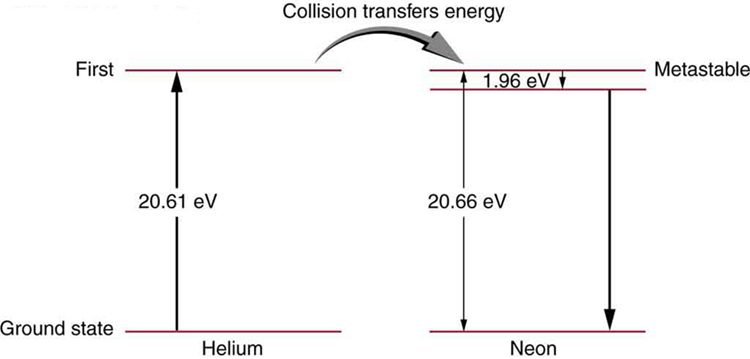
59. Figure shows the energy-level diagram for neon.
(a) Verify that the energy of the photon emitted when neon goes from its metastable state to the one immediately below is equal to 1.96 eV.
(b) Show that the wavelength of this radiation is 633 nm.
(c) What wavelength is emitted when the neon makes a direct transition to its ground state?
Solution
(a) 1.96 eV
(b) \(\displaystyle (1240 eV⋅nm)/(1.96 eV)=633 nm\)
(c) 60.0 nm
60. A helium-neon laser is pumped by electric discharge. What wavelength electromagnetic radiation would be needed to pump it? See Figure for energy-level information.
61. Ruby lasers have chromium atoms doped in an aluminum oxide crystal. The energy level diagram for chromium in a ruby is shown in Figure. What wavelength is emitted by a ruby laser?

Chromium atoms in an aluminum oxide crystal have these energy levels, one of which is metastable. This is the basis of a ruby laser. Visible light can pump the atom into an excited state above the metastable state to achieve a population inversion.
Solution
693 nm
62. (a) What energy photons can pump chromium atoms in a ruby laser from the ground state to its second and third excited states?
(b) What are the wavelengths of these photons? Verify that they are in the visible part of the spectrum.
63. Some of the most powerful lasers are based on the energy levels of neodymium in solids, such as glass, as shown in Figure.
(a) What average wavelength light can pump the neodymium into the levels above its metastable state?
(b) Verify that the 1.17 eV transition produces \(\displaystyle 1.06 μm\) radiation.
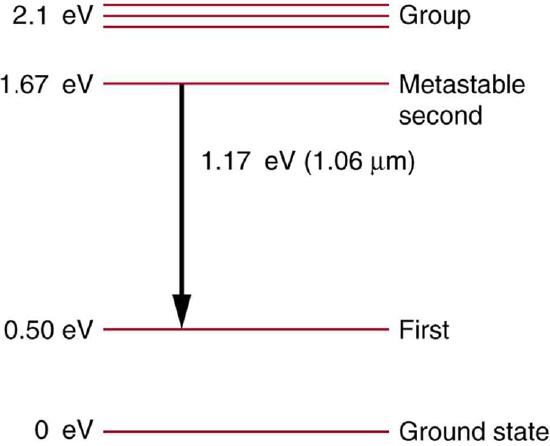
Neodymium atoms in glass have these energy levels, one of which is metastable. The group of levels above the metastable state is convenient for achieving a population inversion, since photons of many different energies can be absorbed by atoms in the ground state.
Solution
(a) 590 nm
(b) \(\displaystyle (1240 eV⋅nm)/(1.17 eV)=1.06 μm\)
30.8: Quantum Numbers and Rules
64. If an atom has an electron in the \(\displaystyle n=5\) state with \(\displaystyle m_l=3\), what are the possible values of \(\displaystyle l\)?
Solution
\(\displaystyle l=4, 3\) are possible since \(\displaystyle l<n\) and \(\displaystyle ∣m_l∣≤l\).
65. An atom has an electron with \(\displaystyle m_l=2\). What is the smallest value of \(\displaystyle n\) for this electron?
66. What are the possible values of \(\displaystyle m_l\) for an electron in the \(\displaystyle n=4\) state?
Solution
\(\displaystyle n=4⇒l=3, 2, 1, 0⇒m_l=±3,±2,±1, 0\) are possible.
67. What, if any, constraints does a value of \(\displaystyle m_l=1\) place on the other quantum numbers for an electron in an atom?
68. (a) Calculate the magnitude of the angular momentum for an \(\displaystyle l=1\) electron.
(b) Compare your answer to the value Bohr proposed for the \(\displaystyle n=1\) state.
Solution
(a) \(\displaystyle 1.49×10^{−34}J⋅s\)
(b) \(\displaystyle 1.06×10^{−34}J⋅s\)
69. (a) What is the magnitude of the angular momentum for an \(\displaystyle l=1\) electron?
(b) Calculate the magnitude of the electron’s spin angular momentum.
(c) What is the ratio of these angular momenta?
70. Repeat Exercise for \(\displaystyle l=3\).
Solution
(a) \(\displaystyle 3.66×10^{−34}J⋅s\)
(b) \(\displaystyle s=9.13×10^{−35}J⋅s\)
(c) \(\displaystyle \frac{L}{S}=\frac{\sqrt{12}}{\sqrt{3/4}}=4\)
71. (a) How many angles can \(\displaystyle L\) make with the z-axis for an \(\displaystyle l=2\) electron?
(b) Calculate the value of the smallest angle.
72. What angles can the spin \(\displaystyle S\)of an electron make with the z-axis?
Solution
\(\displaystyle θ=54.7º, 125.3º\)
30.9: The Pauli Exclusion Principle
73. (a) How many electrons can be in the \(\displaystyle n=4\) shell?
(b) What are its subshells, and how many electrons can be in each?
Solution
(a) 32.
(b) \(\displaystyle 2\) in \(\displaystyle s\), \(\displaystyle 6\) in \(\displaystyle p\),\(\displaystyle 10\) in \(\displaystyle d\), and 14 in \(\displaystyle f\), for a total of 32.
74. (a) What is the minimum value of 1 for a subshell that has 11 electrons in it?
(b) If this subshell is in the \(\displaystyle n=5\) shell, what is the spectroscopic notation for this atom?
75. (a) If one subshell of an atom has 9 electrons in it, what is the minimum value of \(\displaystyle l\)?
(b) What is the spectroscopic notation for this atom, if this subshell is part of the \(\displaystyle n=3\) shell?
Solution
(a) 2
(b) \(\displaystyle 3d^9\)
76. (a) List all possible sets of quantum numbers \(\displaystyle (n,l,m_l,m_s)\) for the \(\displaystyle n=3\) shell, and determine the number of electrons that can be in the shell and each of its subshells.
(b) Show that the number of electrons in the shell equals \(\displaystyle 2n^2\) and that the number in each subshell is \(\displaystyle 2(2l+1)\).
77. Which of the following spectroscopic notations are not allowed? State which rule is violated for each that is not allowed.
(a) \(\displaystyle 5s^1\)
(b) \(\displaystyle 1d^1\)
(c) \(\displaystyle 4s^3\)
(d) \(\displaystyle 3p^7\)
(e) \(\displaystyle 5g^{15}\).
Solution
(b) \(\displaystyle n≥l\) is violated,
(c) cannot have 3 electrons in \(\displaystyle s\) subshell since \(\displaystyle 3>(2l+1)=2\)
(d) cannot have 7 electrons in \(\displaystyle p\) subshell since \(\displaystyle 7>(2l+1)=2(2+1)=6\)
78. Which of the following spectroscopic notations are allowed (that is, which violate none of the rules regarding values of quantum numbers)?
(a) \(\displaystyle 1s^1\)
(b) \(\displaystyle 1d^3\)
(c) \(\displaystyle 4s^2\)
(d) \(\displaystyle 3p^7\)
(e) \(\displaystyle 6h^{20}\)
79. (a) Using the Pauli exclusion principle and the rules relating the allowed values of the quantum numbers \(\displaystyle (n,l,m_l,m_s)\), prove that the maximum number of electrons in a subshell is \(\displaystyle 2n^2\).
(b) In a similar manner, prove that the maximum number of electrons in a shell is \(\displaystyle 2n^2\).
Solution
(a) The number of different values of \(\displaystyle m_l\) is \(\displaystyle ±l,±(l−1),...,0\) for each \(\displaystyle l>0\) and one for \(\displaystyle l=0⇒(2l+1)\). Also an overall factor of 2 since each \(\displaystyle m_l\) can have \(\displaystyle m_s\) equal to either \(\displaystyle +1/2\) or \(\displaystyle −1/2⇒2(2l+1)\).
(b) for each value of \(\displaystyle l\), you get \(\displaystyle 2(2l+1)=0, 1, 2, ...,(n–1)⇒2{[(2)(0)+1]+[(2)(1)+1]+....+[(2)(n−1)+1]}=2[1+3+...+(2n−3)+(2n−1)]\) to see that the expression in the box is \(\displaystyle =n^2\), imagine taking \(\displaystyle (n−1)\) from the last term and adding it to first term \(\displaystyle =2[1+(n–1)+3+...+(2n−3)+(2n−1)–(n−1)]=2[n+3+....+(2n−3)+n]\). Now take \(\displaystyle (n−3)\) from penultimate term and add to the second term \(\displaystyle 2[n+n+...+n+n]=2n^2\).
80. Integrated Concepts
Estimate the density of a nucleus by calculating the density of a proton, taking it to be a sphere 1.2 fm in diameter. Compare your result with the value estimated in this chapter.
81. Integrated Concepts
The electric and magnetic forces on an electron in the CRT in [link] are supposed to be in opposite directions. Verify this by determining the direction of each force for the situation shown. Explain how you obtain the directions (that is, identify the rules used).
Solution
The electric force on the electron is up (toward the positively charged plate). The magnetic force is down (by the RHR).
82. (a) What is the distance between the slits of a diffraction grating that produces a first-order maximum for the first Balmer line at an angle of \(\displaystyle 20.0º\)?
(b) At what angle will the fourth line of the Balmer series appear in first order?
(c) At what angle will the second-order maximum be for the first line?
83. Integrated Concepts
A galaxy moving away from the earth has a speed of \(\displaystyle 0.0100c\). What wavelength do we observe for an \(\displaystyle n_i=7\) to \(\displaystyle n_f=2\) transition for hydrogen in that galaxy?
Solution
401 nm
84. Integrated Concepts
Calculate the velocity of a star moving relative to the earth if you observe a wavelength of 91.0 nm for ionized hydrogen capturing an electron directly into the lowest orbital (that is, a \(\displaystyle n_i=∞\) to \(\displaystyle n_f=1\), or a Lyman series transition).
85. Integrated Concepts
In a Millikan oil-drop experiment using a setup like that in [link], a 500-V potential difference is applied to plates separated by 2.50 cm.
(a) What is the mass of an oil drop having two extra electrons that is suspended motionless by the field between the plates?
(b) What is the diameter of the drop, assuming it is a sphere with the density of olive oil?
Solution
(a) \(\displaystyle 6.54×10^{−16}kg\)
(b) \(\displaystyle 5.54×10^{−7}m\)
86. Integrated Concepts
What double-slit separation would produce a first-order maximum at \(\displaystyle 3.00º\) for 25.0-keV x rays? The small answer indicates that the wave character of x rays is best determined by having them interact with very small objects such as atoms and molecules.
87. Integrated Concepts
In a laboratory experiment designed to duplicate Thomson’s determination of \(\displaystyle q_e/m_e\), a beam of electrons having a velocity of \(\displaystyle 6.00×10^7m/s\) enters a \(\displaystyle 5.00×10^{−3}T\) magnetic field. The beam moves perpendicular to the field in a path having a 6.80-cm radius of curvature. Determine \(\displaystyle q_e/m_e\) from these observations, and compare the result with the known value.
Solution
\(\displaystyle 1.76×10^{11}C/kg\), which agrees with the known value of \(\displaystyle 1.759×10^{11}C/kg\) to within the precision of the measurement
88. Integrated Concepts
Find the value of \(\displaystyle l\), the orbital angular momentum quantum number, for the moon around the earth. The extremely large value obtained implies that it is impossible to tell the difference between adjacent quantized orbits for macroscopic objects.
89. Integrated Concepts
Particles called muons exist in cosmic rays and can be created in particle accelerators. Muons are very similar to electrons, having the same charge and spin, but they have a mass 207 times greater. When muons are captured by an atom, they orbit just like an electron but with a smaller radius, since the mass in \(\displaystyle a_B=\frac{h^2}{4π^2m_ekq^2_e}=0.529×10^{−10}m\) is \(\displaystyle 207 m_e\).
(a) Calculate the radius of the \(\displaystyle n=1\) orbit for a muon in a uranium ion \(\displaystyle (Z=92)\).
(b) Compare this with the 7.5-fm radius of a uranium nucleus. Note that since the muon orbits inside the electron, it falls into a hydrogen-like orbit. Since your answer is less than the radius of the nucleus, you can see that the photons emitted as the muon falls into its lowest orbit can give information about the nucleus.
Solution
(a) 2.78 fm
(b) 0.37 of the nuclear radius.
90. Integrated Concepts
Calculate the minimum amount of energy in joules needed to create a population inversion in a helium-neon laser containing \(\displaystyle 1.00×10^{−4}\) moles of neon.
91. Integrated Concepts
A carbon dioxide laser used in surgery emits infrared radiation with a wavelength of \(\displaystyle 10.6 μm\). In 1.00 ms, this laser raised the temperature of \(\displaystyle 1.00 cm^3\) of flesh to \(\displaystyle 100ºC\) and evaporated it.
(a) How many photons were required? You may assume flesh has the same heat of vaporization as water.
(b) What was the minimum power output during the flash?
Solution
(a) \(\displaystyle 1.34×10^{23}\)
(b) 2.52 MW
92. Integrated Concepts
Suppose an MRI scanner uses 100-MHz radio waves.
(a) Calculate the photon energy.
(b) How does this compare to typical molecular binding energies?
93. Integrated Concepts
(a) An excimer laser used for vision correction emits 193-nm UV. Calculate the photon energy in eV.
(b) These photons are used to evaporate corneal tissue, which is very similar to water in its properties. Calculate the amount of energy needed per molecule of water to make the phase change from liquid to gas. That is, divide the heat of vaporization in kJ/kg by the number of water molecules in a kilogram.
(c) Convert this to eV and compare to the photon energy. Discuss the implications.
Solution
(a) 6.42 eV
(b) \(\displaystyle 7.27×10^{−20}J/molecule\)
(c) 0.454 eV, 14.1 times less than a single UV photon. Therefore, each photon will evaporate approximately 14 molecules of tissue. This gives the surgeon a rather precise method of removing corneal tissue from the surface of the eye.
94. Integrated Concepts
A neighboring galaxy rotates on its axis so that stars on one side move toward us as fast as 200 km/s, while those on the other side move away as fast as 200 km/s. This causes the EM radiation we receive to be Doppler shifted by velocities over the entire range of ±200 km/s. What range of wavelengths will we observe for the 656.0-nm line in the Balmer series of hydrogen emitted by stars in this galaxy. (This is called line broadening.)
95. Integrated Concepts
A pulsar is a rapidly spinning remnant of a supernova. It rotates on its axis, sweeping hydrogen along with it so that hydrogen on one side moves toward us as fast as 50.0 km/s, while that on the other side moves away as fast as 50.0 km/s. This means that the EM radiation we receive will be Doppler shifted over a range of \(\displaystyle ±50.0 km/s\). What range of wavelengths will we observe for the 91.20-nm line in the Lyman series of hydrogen? (Such line broadening is observed and actually provides part of the evidence for rapid rotation.)
Solution
91.18 nm to 91.22 nm
96. Integrated Concepts
Prove that the velocity of charged particles moving along a straight path through perpendicular electric and magnetic fields is \(\displaystyle v=E/B\). Thus crossed electric and magnetic fields can be used as a velocity selector independent of the charge and mass of the particle involved.
97. Unreasonable Results
(a) What voltage must be applied to an X-ray tube to obtain 0.0100-fm-wavelength X-rays for use in exploring the details of nuclei?
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
Solution
(a) \(\displaystyle 1.24×10^{11}V\)
(b) The voltage is extremely large compared with any practical value.
(c) The assumption of such a short wavelength by this method is unreasonable.
98. Unreasonable Results
A student in a physics laboratory observes a hydrogen spectrum with a diffraction grating for the purpose of measuring the wavelengths of the emitted radiation. In the spectrum, she observes a yellow line and finds its wavelength to be 589 nm.
(a) Assuming this is part of the Balmer series, determine \(\displaystyle n_i\), the principal quantum number of the initial state.
(b) What is unreasonable about this result?
(c) Which assumptions are unreasonable or inconsistent?
99. Construct Your Own Problem
The solar corona is so hot that most atoms in it are ionized. Consider a hydrogen-like atom in the corona that has only a single electron. Construct a problem in which you calculate selected spectral energies and wavelengths of the Lyman, Balmer, or other series of this atom that could be used to identify its presence in a very hot gas. You will need to choose the atomic number of the atom, identify the element, and choose which spectral lines to consider.
100. Construct Your Own Problem
Consider the Doppler-shifted hydrogen spectrum received from a rapidly receding galaxy. Construct a problem in which you calculate the energies of selected spectral lines in the Balmer series and examine whether they can be described with a formula like that in the equation \(\displaystyle \frac{1}{λ}=R(\frac{1}{n^2_f}−\frac{1}{n^2_i})\), but with a different constant \(\displaystyle R\).
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


