9.E: Statics and Torque (Exercises)
- Last updated
- Save as PDF
- Page ID
- 10287
Conceptual Questions
9.1: The First Condition for Equilibrium
1. What can you say about the velocity of a moving body that is in dynamic equilibrium? Draw a sketch of such a body using clearly labeled arrows to represent all external forces on the body.
2. Under what conditions can a rotating body be in equilibrium? Give an example.
9.2: The Second Condition for Equilibrium
3. What three factors affect the torque created by a force relative to a specific pivot point?
4. A wrecking ball is being used to knock down a building. One tall unsupported concrete wall remains standing. If the wrecking ball hits the wall near the top, is the wall more likely to fall over by rotating at its base or by falling straight down? Explain your answer. How is it most likely to fall if it is struck with the same force at its base? Note that this depends on how firmly the wall is attached at its base.
5. Mechanics sometimes put a length of pipe over the handle of a wrench when trying to remove a very tight bolt. How does this help? (It is also hazardous since it can break the bolt.)
9.3: Stability
6. A round pencil lying on its side as in Figure is in neutral equilibrium relative to displacements perpendicular to its length. What is its stability relative to displacements parallel to its length?
7. Explain the need for tall towers on a suspension bridge to ensure stable equilibrium.
9.4: Applications of Statics, Including Problem-Solving Strategies
8. When visiting some countries, you may see a person balancing a load on the head. Explain why the center of mass of the load needs to be directly above the person’s neck vertebrae.
9.5: Simple Machines
9. Scissors are like a double-lever system. Which of the simple machines in Figure and Figure is most analogous to scissors?
10. Suppose you pull a nail at a constant rate using a nail puller as shown in Figure. Is the nail puller in equilibrium? What if you pull the nail with some acceleration – is the nail puller in equilibrium then? In which case is the force applied to the nail puller larger and why?
11. Why are the forces exerted on the outside world by the limbs of our bodies usually much smaller than the forces exerted by muscles inside the body?
12. Explain why the forces in our joints are several times larger than the forces we exert on the outside world with our limbs. Can these forces be even greater than muscle forces (see previous Question)?
9.6: Forces and Torques in Muscles and Joints
13. Why are the forces exerted on the outside world by the limbs of our bodies usually much smaller than the forces exerted by muscles inside the body?
14. Explain why the forces in our joints are several times larger than the forces we exert on the outside world with our limbs. Can these forces be even greater than muscle forces?
15. Certain types of dinosaurs were bipedal (walked on two legs). What is a good reason that these creatures invariably had long tails if they had long necks?
16. Swimmers and athletes during competition need to go through certain postures at the beginning of the race. Consider the balance of the person and why start-offs are so important for races.
17. If the maximum force the biceps muscle can exert is 1000 N, can we pick up an object that weighs 1000 N? Explain your answer.
18. Suppose the biceps muscle was attached through tendons to the upper arm close to the elbow and the forearm near the wrist. What would be the advantages and disadvantages of this type of construction for the motion of the arm?
19. Explain one of the reasons why pregnant women often suffer from back strain late in their pregnancy.
Problems & Exercises
9.2: The Second Condition for Equilibrium
20. (a) When opening a door, you push on it perpendicularly with a force of 55.0 N at a distance of 0.850m from the hinges. What torque are you exerting relative to the hinges?
(b) Does it matter if you push at the same height as the hinges?
Solution
a) 46.8 N⋅m
b) It does not matter at what height you push. The torque depends on only the magnitude of the force applied and the perpendicular distance of the force’s application from the hinges. (Children don’t have a tougher time opening a door because they push lower than adults, they have a tougher time because they don’t push far enough from the hinges.)
21. When tightening a bolt, you push perpendicularly on a wrench with a force of 165 N at a distance of 0.140 m from the center of the bolt.
(a) How much torque are you exerting in newton × meters (relative to the center of the bolt)?
(b) Convert this torque to footpounds.
22. Two children push on opposite sides of a door during play. Both push horizontally and perpendicular to the door. One child pushes with a force of 17.5 N at a distance of 0.600 m from the hinges, and the second child pushes at a distance of 0.450 m. What force must the second child exert to keep the door from moving? Assume friction is negligible.
Solution
23.3 N
23. Use the second condition for equilibrium (\(\displaystyle net τ = 0\)) to calculate \(\displaystyle F_p\) in Example, employing any data given or solved for in part (a) of the example.
24. Repeat the seesaw problem in Example with the center of mass of the seesaw 0.160 m to the left of the pivot (on the side of the lighter child) and assuming a mass of 12.0 kg for the seesaw. The other data given in the example remain unchanged. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium.
Solution
Given:
\(\displaystyle m_1=26.0 kg,m_2=32.0 kg,m_s=12.0 kg,\)
\(\displaystyle r_1=1.60 m,r_s=0.160 m,\) find \(\displaystyle (a)r_2,(b)Fp\)
a) Since children are balancing:
net \(\displaystyle τ_{cw}=–\)net\(\displaystyle τ_{ccw}⇒w_1r_1+m_sgr_s=w_2r_2\)
So, solving for \(r^2\)gives:
\(\displaystyle r_2=\frac{w_1r_1+m_sgr_s}{w_2}=\frac{m_1gr_1+m_sgr_s}{m_2g}=\frac{m_1r_1+m_sr_s}{m_2}\)
\(\displaystyle =\frac{(26.0 kg)(1.60 m)+(12.0 kg)(0.160 m)}{32.0 kg}\)
\(\displaystyle =1.36 m\)
b) Since the children are not moving:
net \(\displaystyle F=0=F_p–w_1–w_2–w_s⇒F_p=w_1+w_2+w_s\)
So that
\(\displaystyle F_p=(26.0 kg+32.0 kg+12.0 kg)(9.80m/s^2)=686 N\)
9.3: Stability
25. Suppose a horse leans against a wall as in Figure. Calculate the force exerted on the wall assuming that force is horizontal while using the data in the schematic representation of the situation. Note that the force exerted on the wall is equal in magnitude and opposite in direction to the force exerted on the horse, keeping it in equilibrium. The total mass of the horse and rider is 500 kg. Take the data to be accurate to three digits.
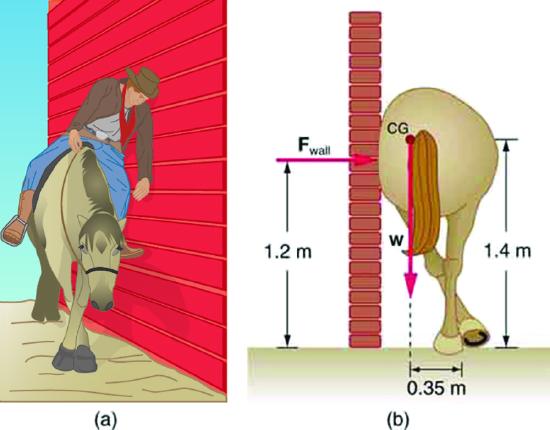
Solution
\(\displaystyle F_{wall}=1.43×10^3N\)
26. Two children of mass 20.0 kg and 30.0 kg sit balanced on a seesaw with the pivot point located at the center of the seesaw. If the children are separated by a distance of 3.00 m, at what distance from the pivot point is the small child sitting in order to maintain the balance?
27. (a) Calculate the magnitude and direction of the force on each foot of the horse in Figure (two are on the ground), assuming the center of mass of the horse is midway between the feet. The total mass of the horse and rider is 500kg.
(b) What is the minimum coefficient of friction between the hooves and ground? Note that the force exerted by the wall is horizontal.
Solution
a) \(\displaystyle 2.55×10^3N, 16.3º\) to the left of vertical (i.e., toward the wall)
b) 0.292
28. A person carries a plank of wood 2.00 m long with one hand pushing down on it at one end with a force \(\displaystyle F_1\) and the other hand holding it up at .500 m from the end of the plank with force \(\displaystyle F_2\). If the plank has a mass of 20.0 kg and its center of gravity is at the middle of the plank, what are the magnitudes of the forces \(\displaystyle F_1\) and \(\displaystyle F_2\)?
29. A 17.0-m-high and 11.0-m-long wall under construction and its bracing are shown in Figure. The wall is in stable equilibrium without the bracing but can pivot at its base. Calculate the force exerted by each of the 10 braces if a strong wind exerts a horizontal force of 650 N on each square meter of the wall. Assume that the net force from the wind acts at a height halfway up the wall and that all braces exert equal forces parallel to their lengths. Neglect the thickness of the wall.
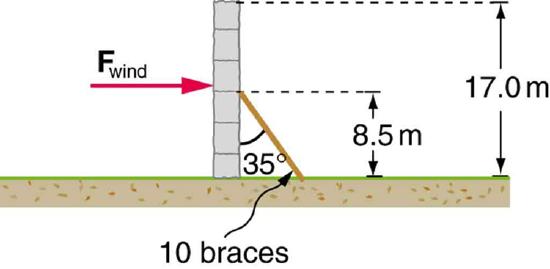
Solution
\(\displaystyle F_B=2.12×10^4N\)
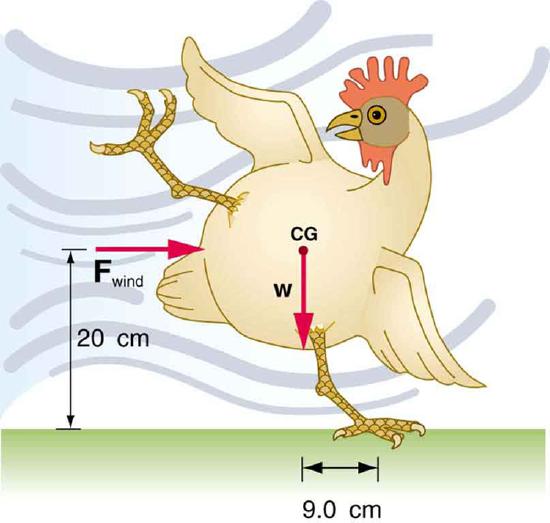
30. (a) What force must be exerted by the wind to support a 2.50-kg chicken in the position shown in Figure?
(b) What is the ratio of this force to the chicken’s weight?
(c) Does this support the contention that the chicken has a relatively stable construction?
31. Suppose the weight of the drawbridge in Figure is supported entirely by its hinges and the opposite shore, so that its cables are slack.
(a) What fraction of the weight is supported by the opposite shore if the point of support is directly beneath the cable attachments?
(b) What is the direction and magnitude of the force the hinges exert on the bridge under these circumstances? The mass of the bridge is 2500 kg.
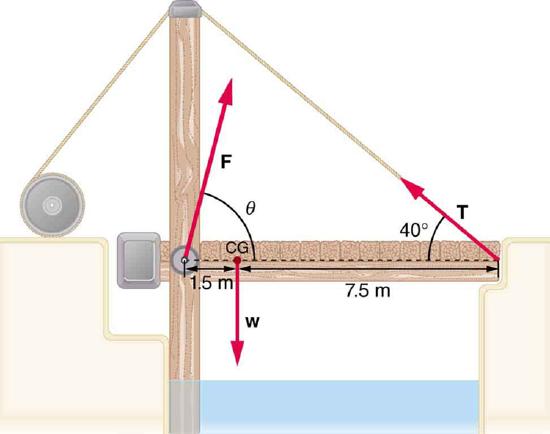
A small drawbridge, showing the forces on the hinges (\(\displaystyle F\)), its weight (\(\displaystyle w\)), and the tension in its wires (\(\displaystyle T\)).
Solution
a) 0.167, or about one-sixth of the weight is supported by the opposite shore.
b) \(\displaystyle F=2.0×10^4N\), straight up.
32. Suppose a 900-kg car is on the bridge in Figure with its center of mass halfway between the hinges and the cable attachments. (The bridge is supported by the cables and hinges only.)
(a) Find the force in the cables.
(b) Find the direction and magnitude of the force exerted by the hinges on the bridge.
33. A sandwich board advertising sign is constructed as shown in Figure. The sign’s mass is 8.00 kg.
(a) Calculate the tension in the chain assuming no friction between the legs and the sidewalk.
(b) What force is exerted by each side on the hinge?
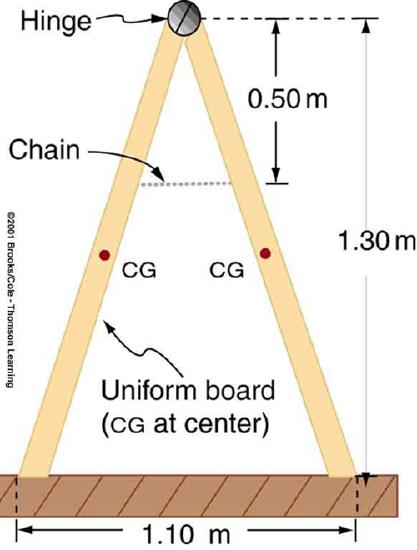
A sandwich board advertising sign demonstrates tension.
Solution
a) 21.6 N
b) 21.6 N
34. (a) What minimum coefficient of friction is needed between the legs and the ground to keep the sign in Figure in the position shown if the chain breaks?
(b) What force is exerted by each side on the hinge?
35. A gymnast is attempting to perform splits. From the information given in Figure, calculate the magnitude and direction of the force exerted on each foot by the floor.
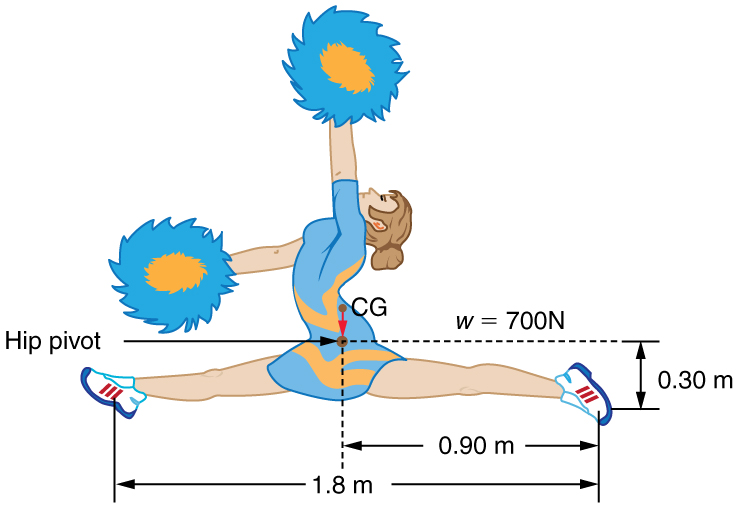
A gymnast performs full split. The center of gravity and the various distances from it are shown.
Solution
350 N directly upwards
9.4: Applications of Statics, Including Problem-Solving Strategies
36. To get up on the roof, a person (mass 70.0 kg) places a 6.00-m aluminum ladder (mass 10.0 kg) against the house on a concrete pad with the base of the ladder 2.00 m from the house. The ladder rests against a plastic rain gutter, which we can assume to be frictionless. The center of mass of the ladder is 2 m from the bottom. The person is standing 3 m from the bottom. What are the magnitudes of the forces on the ladder at the top and bottom?
37. In Figure, the cg of the pole held by the pole vaulter is 2.00 m from the left hand, and the hands are 0.700 m apart. Calculate the force exerted by
(a) his right hand and
(b) his left hand.
(c) If each hand supports half the weight of the pole in Figure, show that the second condition for equilibrium (net \(\displaystyle τ=0\)) is satisfied for a pivot other than the one located at the center of gravity of the pole. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium described above.
9.5: Simple Machines
38. What is the mechanical advantage of a nail puller—similar to the one shown in Figure —where you exert a force 45 cm from the pivot and the nail is 1.8 cm on the other side? What minimum force must you exert to apply a force of 1250 N to the nail?
Solution
25
50 N
39. Suppose you needed to raise a 250-kg mower a distance of 6.0 cm above the ground to change a tire. If you had a 2.0-m long lever, where would you place the fulcrum if your force was limited to 300 N?
40. a) What is the mechanical advantage of a wheelbarrow, such as the one in Figure, if the center of gravity of the wheelbarrow and its load has a perpendicular lever arm of 5.50 cm, while the hands have a perpendicular lever arm of 1.02 m?
(b) What upward force should you exert to support the wheelbarrow and its load if their combined mass is 55.0 kg?
(c) What force does the wheel exert on the ground?
Solution
a) \(\displaystyle MA=18.5\)
b) \(\displaystyle F_i=29.1 N\)
c) 510 N downward
41. A typical car has an axle with \(\displaystyle 1.10 cm\) radius driving a tire with a radius of \(\displaystyle 27.5 cm\). What is its mechanical advantage assuming the very simplified model in Figure(b)?
42. What force does the nail puller in Exercise exert on the supporting surface? The nail puller has a mass of 2.10 kg.
Solution
\(\displaystyle 1.3×10^3N\)
43. If you used an ideal pulley of the type shown in Figure(a) to support a car engine of mass 115 kg,
(a) What would be the tension in the rope?
(b) What force must the ceiling supply, assuming you pull straight down on the rope? Neglect the pulley system’s mass.
44. Repeat Exercise for the pulley shown in Figure(c), assuming you pull straight up on the rope. The pulley system’s mass is 7.00 kg .
Solution
a) \(\displaystyle T=299 N\)
b) 897 N upward
9.6: Forces and Torques in Muscles and Joints
45. Verify that the force in the elbow joint in Example is 407 N, as stated in the text.
Solution
\(\displaystyle F_B=470 N;r_1=4.00 cm;w_a=2.50 kg;r_2=16.0 cm;w_b=4.00 kg;r_3=38.0 cm\)
\(\displaystyle F_E=w_a(\frac{r_2}{r_1}−1)+w_b(\frac{r_3}{r_1}−1)\)
\(\displaystyle =(2.50 kg)(9.80m/s^2)(\frac{16.0 cm}{4.0 cm}–1)+(4.00 kg)(9.80m/s^2)(\frac{38.0 cm}{4.00 cm}–1)\)
\(\displaystyle =407 N\)
46. Two muscles in the back of the leg pull on the Achilles tendon as shown in Figure. What total force do they exert?
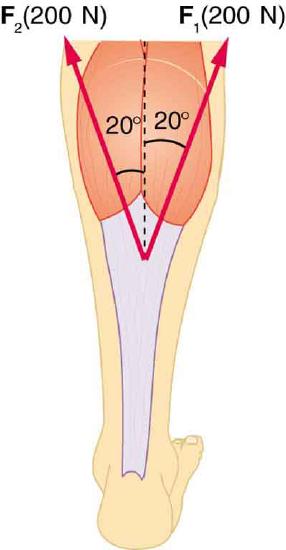
The Achilles tendon of the posterior leg serves to attach plantaris, gastrocnemius, and soleus muscles to calcaneus bone.
47. The upper leg muscle (quadriceps) exerts a force of 1250 N, which is carried by a tendon over the kneecap (the patella) at the angles shown in Figure. Find the direction and magnitude of the force exerted by the kneecap on the upper leg bone (the femur).
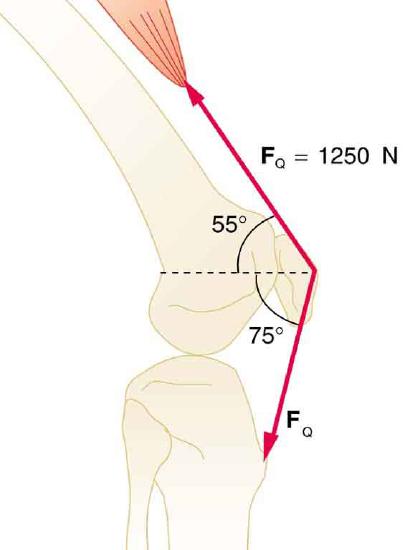
The knee joint works like a hinge to bend and straighten the lower leg. It permits a person to sit, stand, and pivot.
Solution
\(\displaystyle 1.1×10^3N\) \(\displaystyle θ=190º\) ccw from positive x axis
48. A device for exercising the upper leg muscle is shown in Figure, together with a schematic representation of an equivalent lever system. Calculate the force exerted by the upper leg muscle to lift the mass at a constant speed. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium in Applications of Statistics, Including Problem-Solving Strategies.
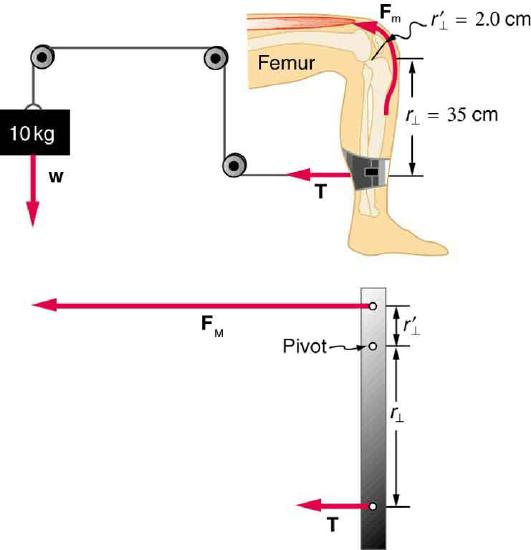
A mass is connected by pulleys and wires to the ankle in this exercise device.
49. A person working at a drafting board may hold her head as shown in Figure, requiring muscle action to support the head. The three major acting forces are shown. Calculate the direction and magnitude of the force supplied by the upper vertebrae \(\displaystyle F_V\) to hold the head stationary, assuming that this force acts along a line through the center of mass as do the weight and muscle force.
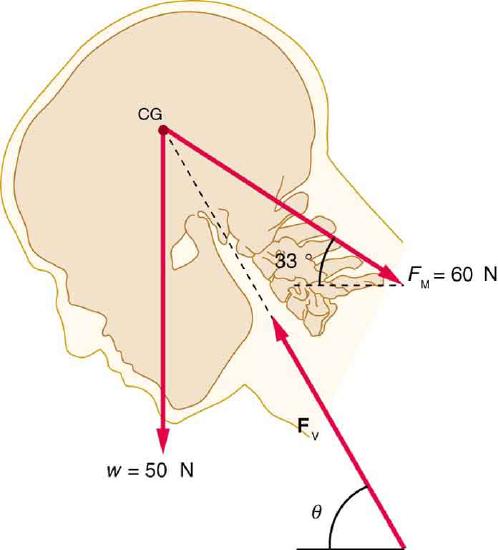
Solution
\(\displaystyle F_V=97N,θ=59º\)
50. We analyzed the biceps muscle example with the angle between forearm and upper arm set at 90º. Using the same numbers as in Example, find the force exerted by the biceps muscle when the angle is 120º and the forearm is in a downward position.
51. Even when the head is held erect, as in Figure, its center of mass is not directly over the principal point of support (the atlanto-occipital joint). The muscles at the back of the neck should therefore exert a force to keep the head erect. That is why your head falls forward when you fall asleep in the class.
(a) Calculate the force exerted by these muscles using the information in the figure.
(b) What is the force exerted by the pivot on the head?
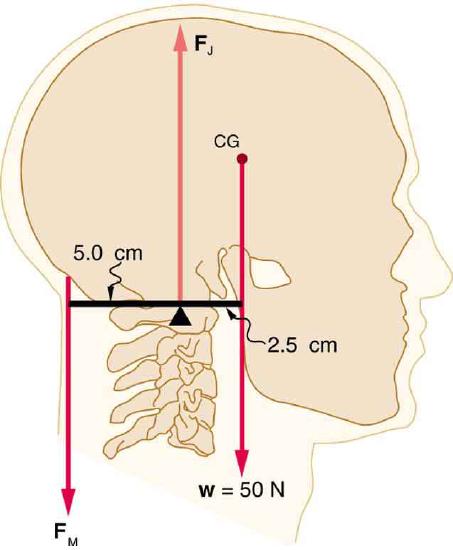
The center of mass of the head lies in front of its major point of support, requiring muscle action to hold the head erect. A simplified lever system is shown.
Solution
(a) 25 N downward
(b) 75 N upward
52. A 75-kg man stands on his toes by exerting an upward force through the Achilles tendon, as in Figure.
(a) What is the force in the Achilles tendon if he stands on one foot?
(b) Calculate the force at the pivot of the simplified lever system shown—that force is representative of forces in the ankle joint.
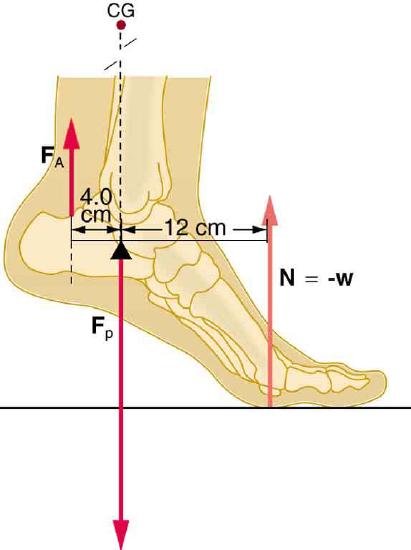
The muscles in the back of the leg pull the Achilles tendon when one stands on one’s toes. A simplified lever system is shown.
Solution
(a) \(\displaystyle F_A=2.21×10^3N\) upward
(b) \(\displaystyle F_B=2.94×10^3N\) downward
53. A father lifts his child as shown in Figure. What force should the upper leg muscle exert to lift the child at a constant speed?
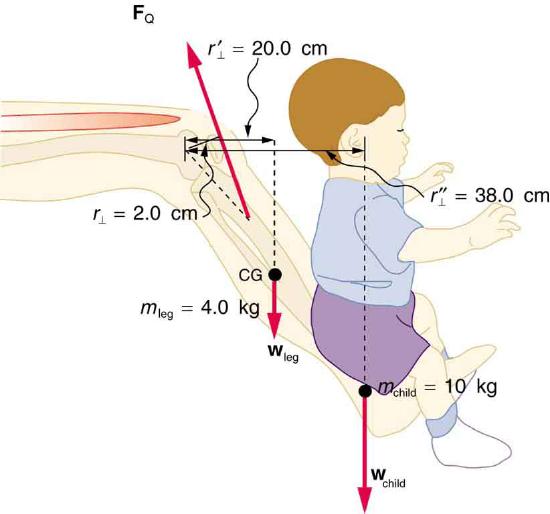
A child being lifted by a father’s lower leg.
54. Unlike most of the other muscles in our bodies, the masseter muscle in the jaw, as illustrated in Figure, is attached relatively far from the joint, enabling large forces to be exerted by the back teeth.
(a) Using the information in the figure, calculate the force exerted by the lower teeth on the bullet.
(b) Calculate the force on the joint.
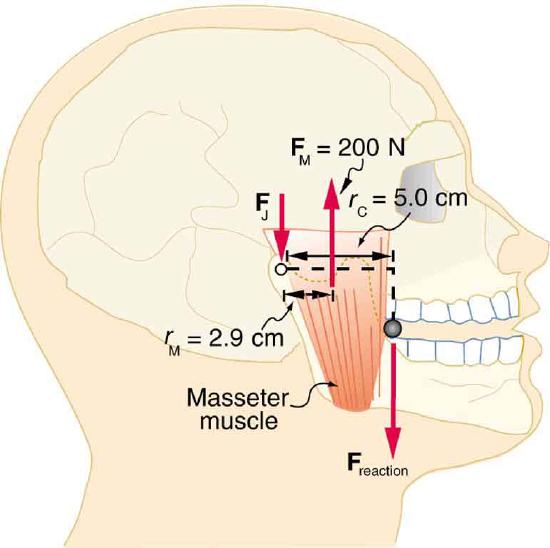
A person clenching a bullet between his teeth.
Solution
(a) \(\displaystyle F_{\text{teeth on bullet}}=1.2×10^2N\) upward
(b) \(\displaystyle F_J=84 N\) downward
55. Integrated Concepts
Suppose we replace the 4.0-kg book in Exercise of the biceps muscle with an elastic exercise rope that obeys Hooke’s Law. Assume its force constant \(\displaystyle k=600N/m\).
(a) How much is the rope stretched (past equilibrium) to provide the same force \(\displaystyle F_B\) as in this example? Assume the rope is held in the hand at the same location as the book.
(b) What force is on the biceps muscle if the exercise rope is pulled straight up so that the forearm makes an angle of \(\displaystyle 25º\)with the horizontal? Assume the biceps muscle is still perpendicular to the forearm.
56. (a) What force should the woman in Figure exert on the floor with each hand to do a push-up? Assume that she moves up at a constant speed.
(b) The triceps muscle at the back of her upper arm has an effective lever arm of 1.75 cm, and she exerts force on the floor at a horizontal distance of 20.0 cm from the elbow joint. Calculate the magnitude of the force in each triceps muscle, and compare it to her weight.
(c) How much work does she do if her center of mass rises 0.240 m? (d) What is her useful power output if she does 25 pushups in one minute?
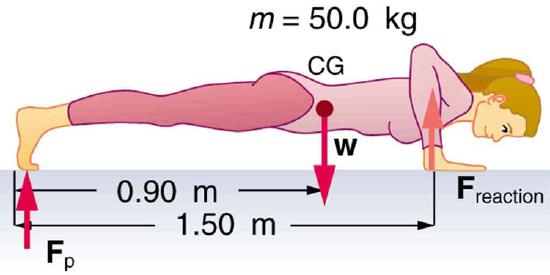
A woman doing pushups.
Solution
(a) 147 N downward
(b) 1680 N, 3.4 times her weight
(c) 118 J
(d) 49.0 W
57. You have just planted a sturdy 2-m-tall palm tree in your front lawn for your mother’s birthday. Your brother kicks a 500 g ball, which hits the top of the tree at a speed of 5 m/s and stays in contact with it for 10 ms. The ball falls to the ground near the base of the tree and the recoil of the tree is minimal.
(a) What is the force on the tree?
(b) The length of the sturdy section of the root is only 20 cm. Furthermore, the soil around the roots is loose and we can assume that an effective force is applied at the tip of the 20 cm length. What is the effective force exerted by the end of the tip of the root to keep the tree from toppling? Assume the tree will be uprooted rather than bend.
(c) What could you have done to ensure that the tree does not uproot easily?
58. Unreasonable Results
Suppose two children are using a uniform seesaw that is 3.00 m long and has its center of mass over the pivot. The first child has a mass of 30.0 kg and sits 1.40 m from the pivot.
(a) Calculate where the second 18.0 kg child must sit to balance the seesaw.
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent?
Solution
a) \(\displaystyle \bar{x}_2=2.33 m\)
b) The seesaw is 3.0 m long, and hence, there is only 1.50 m of board on the other side of the pivot. The second child is off the board.
c) The position of the first child must be shortened, i.e. brought closer to the pivot.
59. Construct Your Own Problem
Consider a method for measuring the mass of a person’s arm in anatomical studies. The subject lies on her back, extends her relaxed arm to the side and two scales are placed below the arm. One is placed under the elbow and the other under the back of her hand. Construct a problem in which you calculate the mass of the arm and find its center of mass based on the scale readings and the distances of the scales from the shoulder joint. You must include a free body diagram of the arm to direct the analysis. Consider changing the position of the scale under the hand to provide more information, if needed. You may wish to consult references to obtain reasonable mass values.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

