01. Concepts and Principles
( \newcommand{\kernel}{\mathrm{null}\,}\)
If the forces acting on an object are not constant, then the acceleration of the object is not constant. To analyze the kinematics of an object undergoing non-constant acceleration requires the use of calculus. By re-examining our original definitions, valid in the limit of very small time intervals during which the acceleration is approximately constant, the relationships between position, velocity, and acceleration can be constructed in terms of the derivative.
Position (r)
Let r(t) be the location of the object at every time, t, in the time interval of interest.
Velocity (v)
Our original definition of velocity,
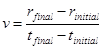
remains valid if the acceleration is constant. The acceleration will always be constant in the limit of infinitesimally small time intervals. By the fundamental definition of calculus, the above expression, in the limit of infinitesimally small time intervals, becomes the derivative of the position function. Thus, v(t), the velocity of the object at every time, t, is defined to be the derivative of the position function, r(t).
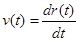
Acceleration (a)
Our original definition of acceleration,
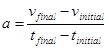
also remains valid only in the limit of infinitesimally small time intervals. By the fundamental definition of calculus, the above expression, in the limit of infinitesimally small time intervals, becomes the derivative of the velocity function. Thus, a(t), the acceleration of the object at every time, t, is defined to be the derivative of the velocity function, v(t).
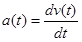
Thus, if the position of the object is known as a function of time, the velocity and acceleration functions can be constructed through differentiation of r(t).
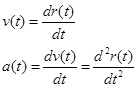
On the other hand, if the acceleration of the object is known as a function of time, the velocity and position functions can be constructed through anti-differentiation, or integration, of a(t).
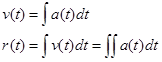
An important distinction, however, is that when integrating a(t) to form v(t), an arbitrary constant will be introduced into the expression for v(t). This constant can often be determined from knowledge of the object’s velocity at some specific instant in time. Another integration, to form r(t), will introduce an additional arbitrary constant that can often be determined from knowledge of the object’s position at some specific instant in time.
In closing, please remember that the kinematic relations that have been used throughout this course were derived assuming a constant acceleration. If the acceleration is not constant, those relations are incorrect, and the correct kinematic relationships must be determined through direct integration and differentiation.


