03. Elastic Potential Energy

1. Elastic Potential Energy
2. Applying the Work-Energy Relation with Elastic Potential Energy

Elastic Potential Energy

When an object interacts with a spring, or other elastic material, a common model is that the material reacts linearly, i.e., with a force directly proportional to the deformation of the material. It is possible to calculate the work done by the linear material in general, and to rewrite the work-energy relation in such a way as to incorporate the effects of this work from the start. This is referred to as constructing a potential energy function for the work done by the elastic material. We did exactly the same thing earlier for the force of gravity. Imagine a spring of spring constant k, initially deformed by a distance s_i. It changes its deformation, ultimately resulting in deformation s_f. To calculate the work done by the spring on the object causing the deformation:

\[ Work = \int_{r_i}^{r_f}F \; cos \phi \; dr \]

\[ Work = \int_{r_i}^{r_f}(-ks) cos \phi \; dr \]

Choosing a coordinate system in which s and r are interchangeable (the origin is located at the point where the spring is at its natural length and the direction of elongation is positive) and allowing the force and the displacement to be in the same direction (f = 0) results in,

\[ Work = \int_{r_i}^{r_f}(-ks) cos 0 \; dr \]

\[ Work = -\dfrac{1}{2} k s_f^2 + \dfrac{1}{2}S_i^2 \]

The terms, ¹/₂ks², are referred to as elastic potential energy. Inserting this result into the work-energy relation results in

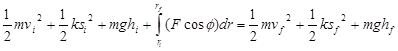
with the understanding that the forces remaining in the equation, which may do work on the system, do not include the force of gravity or the force of the spring. The work done by the force of gravity and the force of the spring are already included in the relation via the inclusion of the potential energy terms.

Applying the Work-Energy Relation with Elastic Potential Energy

A 0.15 kg ball is launched vertically upward by means of a spring-loaded plunger, pulled back 8.0 cm and released. It requires a force of about 10 N to push the plunger back 8.0 cm.

The spring constant of the plunger is known to be 125 N/m from above. Applying the work-energy relation with potential energy terms between the instant the plunger is released and the instant the ball reaches its maximum height results in

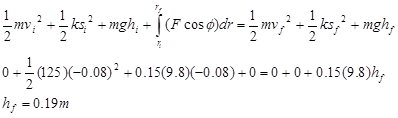
Of course, this results in the same answer as before.

Paul D’Alessandris (Monroe Community College)