04. Analysis Tools 3
( \newcommand{\kernel}{\mathrm{null}\,}\)
Applying the Impulse-Momentum Relation to a Collision
Probably the most useful application of the impulse-momentum relation is in the study of collisions. For example:
Far from the earth, a 250 kg space probe, moving at 5 km/s, collides head-on with a 65 kg piece of space debris initially at rest. The debris becomes entangled in the probe’s solar collectors.
Let’s choose:
Event 1: The instant before the collision.
Event 2: The instant the debris and probe reach a common velocity.
The free-body diagrams for the two objects during this time interval are shown below.
Applying the impulse-momentum relation to each object separately yields:
Notice that the final velocities of the two objects are the same, because they remain joined together following the collision. Also, the Dt’s are the same because the time interval over which the force of the debris acts on the probe must be the same as the time interval over which the force of the probe acts on the debris. In fact, these two forces must be equal to each other in magnitude by Newton’s Third Law.
Thus, the impulses must cancel if the two equations are added together:
The probe slows to a speed of 4032 m/s (and the debris changes direction and accelerates to a speed of 4032 m/s) via the collision. Thus, even though we do not know the magnitude of the force involved, or the duration of the collision, we can calculate the final velocities of the two objects colliding. This is because the forces involved comprise an interaction, and by Newton’s Third Law forces that comprise an interaction are always equal in magnitude and opposite in direction.
In fact, in problems involving collisions (or explosions, which to physicists are merely collisions played backward in time!), you should almost always apply the impulse-momentum relation to the interacting objects because the forces involved comprise an interaction. Thus, by adding your equations together, these terms will always add to zero. This will often allow you to determine the final velocities of the colliding objects.
In conclusion, I should point out that the probe loses momentum during the collision and that the debris gains the exact same amount of momentum (check the numbers to verify this statement). The momentum is transferred from the probe to the debris through the action of the impulse the probe and debris exert on each other. The momentum transfer from the probe to the debris is analogous to throwing a wooden block from the playroom into the yard: The playroom now has one less block and the yard has one more!
Applying the Work-Energy Relation to the Same Collision
Let’s return to the collision scenario discussed above and attempt to investigate it using work-energy.
Far from the earth, a 250 kg space probe, moving at 5 km/s, collides head-on with a 65 kg piece of space debris initially at rest. The debris becomes entangled in the probe’s solar collectors.
Let’s choose:
Event 1: The instant before the collision.
Event 2: The instant the debris and probe reach a common velocity.
The free-body diagrams for the two objects during this time interval are shown below.
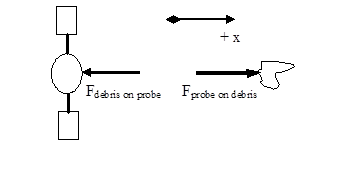
Applying the work-energy relation to each object separately yields:
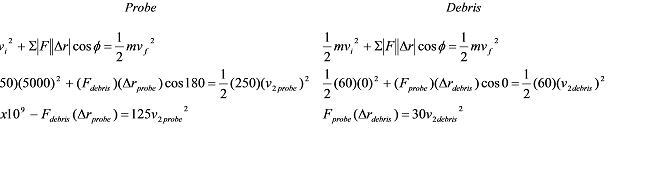
The final velocities of the two objects are the same, because they remain joined together following the collision, and the two forces are the same by Newton’s Third Law. However, these two equations can not be added together and solved because the two distances over which the forces act, Drprobe and Drdebris, are not necessarily equal. During the collision, the center of the probe will move a different distance that the center of the debris[1]. Since these two distances are different, the works willnot cancel as the impulses did, and the equations are not solvable!
In fact, since we know v2 = 4032 m/s from our momentum analysis,
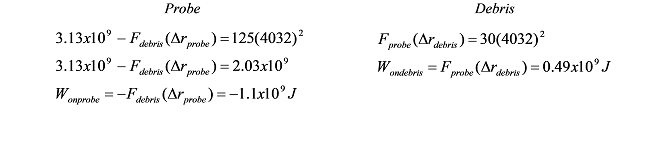
Obviously, the two works do not cancel. In fact, the internal work, or work done by the objects on each other, totals -0.61 x 109 J. This means that there is 0.61 x 109 J less kinetic energy in the system of the probe and the debris after the collision than before the collision. This is sometimes referred to as the energy lost in the collision, although the energy is not lost but rather converted into other forms of energy (i.e., other hiding places for the wooden blocks that have yet to be discussed), such as thermal energy.
In short, the work-energy relation (as it now stands) can not be used to effectively analyze collisions unless additional information regarding the internal energy is available. Occasionally, an approximation is made in which the total internal work is zero. When this approximation is made, the collision is referred to as an elastic collision. Realistic collisions, in which the total internal energy is not zero and kinetic energy is “lost”, are referred to as inelastic collisions. In other words, during an elastic collision the two objects “bounce apart” whereas during an inelastic collision they “stick together.”
[1] If the two objects were actually particles, rather than beingapproximated as particles, then the two distances would have to be the same and the two works would cancel when the equation were added together.


