03. Using the Calculus Another Example

1. Another Example

Another Example

Investigate the scenario described below.

A sports car can accelerate from rest to a speed of 40 m/s while traveling a distance of 200 m. Assume the acceleration of the car can be modeled as a decreasing linear function of time, with a maximum acceleration of 10.4 m/s².

Between event 1 and 2, the car's acceleration can be modeled by a generic linear function of time, or

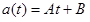
Since the acceleration is decreasing, the maximum value occurs at t = 0 s,

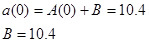
Since we don’t know the value of the acceleration at t₂, or even the value of t₂, we can’t determine A, and all we can currently say about the acceleration function is that it is given by:

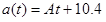
Nonetheless, we can still integrate the acceleration to determine the velocity,

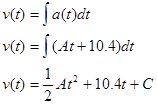
Since we know v = 0 m/s when t = 0 s, we can determine the integration constant:

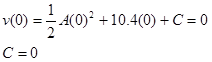
We also know that v = 40 m/s at t₂, so:

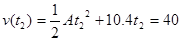
This equation can’t be solved, since it involves two unknowns. However, if we can generate a second equation involving the same two unknowns, we can solve the two equations simultaneously. This second equation must involve the position function of the car:

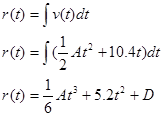
Since we know r = 0 when t = 0 s, we can determine the integration constant:

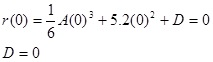
We also know that r = 200 m at t₂, so:

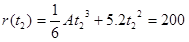
These two equations,

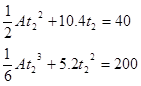
can be solved by substitution (or by using a solver). Solve the first equation for A, and substitute this expression into the second equation. This will result in a quadratic equation for t₂. The solution is t₂ = 7.57 s, the time for the car to reach 40 m/s. Plugging this value back into the original equations allows you to complete the description of the car’s motion.

Paul D’Alessandris (Monroe Community College)