5.E: Further Applications of Newton's Laws (Exercises)
- Last updated
- Jul 6, 2021
- Save as PDF
- Page ID
- 8796
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
5.1: Friction
1. Define normal force. What is its relationship to friction when friction behaves simply?
2. The glue on a piece of tape can exert forces. Can these forces be a type of simple friction? Explain, considering especially that tape can stick to vertical walls and even to ceilings.
3. When you learn to drive, you discover that you need to let up slightly on the brake pedal as you come to a stop or the car will stop with a jerk. Explain this in terms of the relationship between static and kinetic friction.
4. When you push a piece of chalk across a chalkboard, it sometimes screeches because it rapidly alternates between slipping and sticking to the board. Describe this process in more detail, in particular explaining how it is related to the fact that kinetic friction is less than static friction. (The same slip-grab process occurs when tires screech on pavement.)
5.2: Drag Forces
5. Athletes such as swimmers and bicyclists wear body suits in competition. Formulate a list of pros and cons of such suits.
6. Two expressions were used for the drag force experienced by a moving object in a liquid. One depended upon the speed, while the other was proportional to the square of the speed. In which types of motion would each of these expressions be more applicable than the other one?
7. As cars travel, oil and gasoline leaks onto the road surface. If a light rain falls, what does this do to the control of the car? Does a heavy rain make any difference?
8. Why can a squirrel jump from a tree branch to the ground and run away undamaged, while a human could break a bone in such a fall?
5.3: Elasticity: Stress and Strain
9. The elastic properties of the arteries are essential for blood flow. Explain the importance of this in terms of the characteristics of the flow of blood (pulsating or continuous).
10. What are you feeling when you feel your pulse? Measure your pulse rate for 10 s and for 1 min. Is there a factor of 6 difference?
11. Examine different types of shoes, including sports shoes and thongs. In terms of physics, why are the bottom surfaces designed as they are? What differences will dry and wet conditions make for these surfaces?
12. Would you expect your height to be different depending upon the time of day? Why or why not?
13. Why can a squirrel jump from a tree branch to the ground and run away undamaged, while a human could break a bone in such a fall?
14. Explain why pregnant women often suffer from back strain late in their pregnancy.
15. An old carpenter’s trick to keep nails from bending when they are pounded into hard materials is to grip the center of the nail firmly with pliers. Why does this help?
16. When a glass bottle full of vinegar warms up, both the vinegar and the glass expand, but vinegar expands significantly more with temperature than glass. The bottle will break if it was filled to its tightly capped lid. Explain why, and also explain how a pocket of air above the vinegar would prevent the break. (This is the function of the air above liquids in glass containers.)
Problems & Exercises
5.1: Friction
17. A physics major is cooking breakfast when he notices that the frictional force between his steel spatula and his Teflon frying pan is only 0.200 N. Knowing the coefficient of kinetic friction between the two materials, he quickly calculates the normal force. What is it?
Solution
5.00N
18. (a) When rebuilding her car’s engine, a physics major must exert 300 N of force to insert a dry steel piston into a steel cylinder. What is the magnitude of the normal force between the piston and cylinder?
(b) What is the magnitude of the force would she have to exert if the steel parts were oiled?
19. (a) What is the maximum frictional force in the knee joint of a person who supports 66.0 kg of her mass on that knee?
(b) During strenuous exercise it is possible to exert forces to the joints that are easily ten times greater than the weight being supported. What is the maximum force of friction under such conditions? The frictional forces in joints are relatively small in all circumstances except when the joints deteriorate, such as from injury or arthritis. Increased frictional forces can cause further damage and pain.
20. Suppose you have a 120-kg wooden crate resting on a wood floor.
(a) What maximum force can you exert horizontally on the crate without moving it?
(b) If you continue to exert this force once the crate starts to slip, what will the magnitude of its acceleration then be?
Solution
(a) 588 N
(b) 1.96m/s2
21. (a) If half of the weight of a small 1.00×103kg utility truck is supported by its two drive wheels, what is the magnitude of the maximum acceleration it can achieve on dry concrete?
(b) Will a metal cabinet lying on the wooden bed of the truck slip if it accelerates at this rate?
(c) Solve both problems assuming the truck has four-wheel drive.
22. A team of eight dogs pulls a sled with waxed wood runners on wet snow (mush!). The dogs have average masses of 19.0 kg, and the loaded sled with its rider has a mass of 210 kg.
(a) Calculate the magnitude of the acceleration starting from rest if each dog exerts an average force of 185 N backward on the snow.
(b) What is the magnitude of the acceleration once the sled starts to move?
(c) For both situations, calculate the magnitude of the force in the coupling between the dogs and the sled.
Solution
(a) 3.29m/s2
(b) 3.52m/s2
(c) 980 N; 945 N
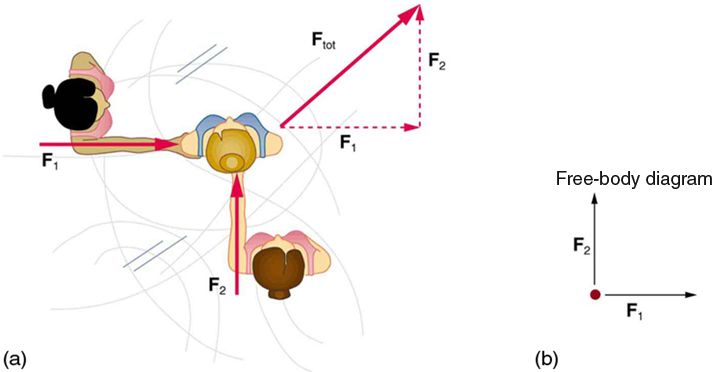
23. Consider the 65.0-kg ice skater being pushed by two others shown in Figure.
(a) Find the direction and magnitude of Ftot, the total force exerted on her by the others, given that the magnitudes F1 and F2 are 26.4 N and 18.6 N, respectively.
(b) What is her initial acceleration if she is initially stationary and wearing steel-bladed skates that point in the direction of Ftot?
(c) What is her acceleration assuming she is already moving in the direction of Ftot? (Remember that friction always acts in the direction opposite that of motion or attempted motion between surfaces in contact.)
24. Show that the acceleration of any object down a frictionless incline that makes an angle θ with the horizontal is a=gsinθ. (Note that this acceleration is independent of mass.)
25. Show that the acceleration of any object down an incline where friction behaves simply (that is, where fk=μkN) is a=g(sinθ−μkcosθ). Note that the acceleration is independent of mass and reduces to the expression found in the previous problem when friction becomes negligibly small (μk=0).
26. Calculate the deceleration of a snow boarder going up a ∗5.0º. slope assuming the coefficient of friction for waxed wood on wet snow. The result of Exercise 25 may be useful, but be careful to consider the fact that the snow boarder is going uphill. Explicitly show how you follow the steps in Problem-Solving Strategies.
Solution
1.83m/s2
27. (a) Calculate the acceleration of a skier heading down a 10.0º slope, assuming the coefficient of friction for waxed wood on wet snow.
(b) Find the angle of the slope down which this skier could coast at a constant velocity. You can neglect air resistance in both parts, and you will find the result of Exercise 25 to be useful. Explicitly show how you follow the steps in the Problem-Solving Strategies.
28. If an object is to rest on an incline without slipping, then friction must equal the component of the weight of the object parallel to the incline. This requires greater and greater friction for steeper slopes. Show that the maximum angle of an incline above the horizontal for which an object will not slide down is θ=tan–1μs. You may use the result of the previous problem. Assume that a=0 and that static friction has reached its maximum value.
29. Calculate the maximum deceleration of a car that is heading down a 6º slope (one that makes an angle of 6º with the horizontal) under the following road conditions. You may assume that the weight of the car is evenly distributed on all four tires and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the deceleration. (Ignore rolling.) Calculate for a car:
(a) On dry concrete.
(b) On wet concrete.
(c) On ice, assuming that μs=0.100, the same as for shoes on ice.
30. Calculate the maximum acceleration of a car that is heading up a 4º slope (one that makes an angle of 4º with the horizontal) under the following road conditions. Assume that only half the weight of the car is supported by the two drive wheels and that the coefficient of static friction is involved—that is, the tires are not allowed to slip during the acceleration. (Ignore rolling.)
(a) On dry concrete.
(b) On wet concrete.
(c) On ice, assuming that μs=0.100, the same as for shoes on ice.
Solution
(a) 4.20m/s2
(b) 2.74m/s2
(c) –0.195m/s2
31. Repeat Exercise for a car with four-wheel drive.
32. A freight train consists of two 8.00×105−kg engines and 45 cars with average masses of 5.50×105kg
(a) What force must each engine exert backward on the track to accelerate the train at a rate of 5.00×10−2m/s2 if the force of friction is 7.50×105N, assuming the engines exert identical forces? This is not a large frictional force for such a massive system. Rolling friction for trains is small, and consequently trains are very energy-efficient transportation systems.
(b) What is the magnitude of the force in the coupling between the 37th and 38th cars (this is the force each exerts on the other), assuming all cars have the same mass and that friction is evenly distributed among all of the cars and engines?
Solution
(a) 1.03×106N
(b) 3.48×105N
33. Consider the 52.0-kg mountain climber in Figure.
(a) Find the tension in the rope and the force that the mountain climber must exert with her feet on the vertical rock face to remain stationary. Assume that the force is exerted parallel to her legs. Also, assume negligible force exerted by her arms.
(b) What is the minimum coefficient of friction between her shoes and the cliff?
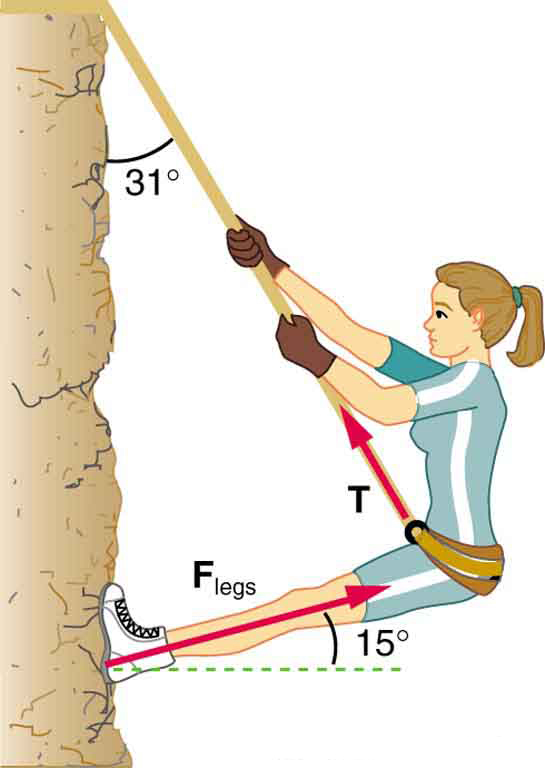
Part of the climber’s weight is supported by her rope and part by friction between her feet and the rock face.
34. A contestant in a winter sporting event pushes a 45.0-kg block of ice across a frozen lake as shown in Figure(a).
(a) Calculate the minimum force F he must exert to get the block moving.
(b) What is the magnitude of its acceleration once it starts to move, if that force is maintained?
Solution
(a) 51.0N
(b) 0.720m/s2
35. Repeat Exercise 34 with the contestant pulling the block of ice with a rope over his shoulder at the same angle above the horizontal as shown in Figure(b).
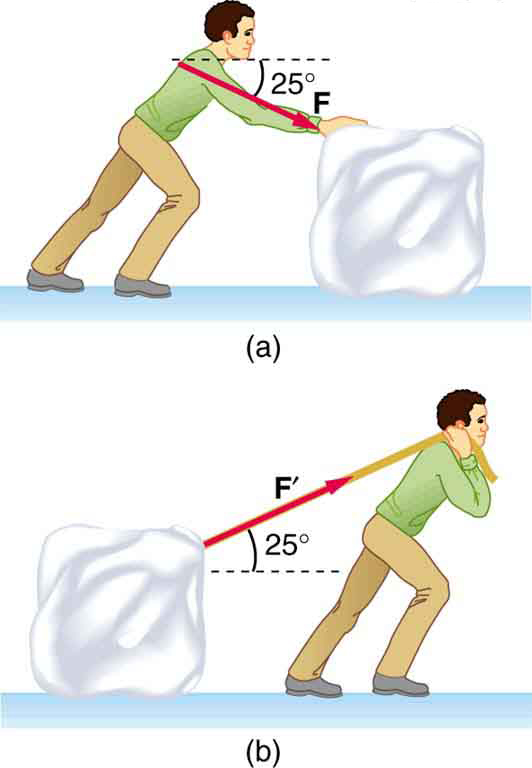
Which method of sliding a block of ice requires less force—(a) pushing or (b) pulling at the same angle above the horizontal?
5.2: Drag Forces
36. The terminal velocity of a person falling in air depends upon the weight and the area of the person facing the fluid. Find the terminal velocity (in meters per second and kilometers per hour) of an 80.0-kg skydiver falling in a pike (headfirst) position with a surface area of 0.140m2..
Solution
115m/s;414km/hr
37. A 60-kg and a 90-kg skydiver jump from an airplane at an altitude of 6000 m, both falling in the pike position. Make some assumption on their frontal areas and calculate their terminal velocities. How long will it take for each skydiver to reach the ground (assuming the time to reach terminal velocity is small)? Assume all values are accurate to three significant digits.
38. A 560-g squirrel with a surface area of 930cm2 falls from a 5.0-m tree to the ground. Estimate its terminal velocity. (Use a drag coefficient for a horizontal skydiver.) What will be the velocity of a 56-kg person hitting the ground, assuming no drag contribution in such a short distance?
Solution
25m/s;9.9m/s
39. To maintain a constant speed, the force provided by a car’s engine must equal the drag force plus the force of friction of the road (the rolling resistance).
(a) What are the magnitudes of drag forces at 70 km/h and 100 km/h for a Toyota Camry? (Drag area is 0.70m2
(b) What is the magnitude of drag force at 70 km/h and 100 km/h for a Hummer H2? (Drag area is 2.44m2) Assume all values are accurate to three significant digits.
40. By what factor does the drag force on a car increase as it goes from 65 to 110 km/h?
Solution
2.9
41. Calculate the speed a spherical rain drop would achieve falling from 5.00 km (a) in the absence of air drag (b) with air drag. Take the size across of the drop to be 4 mm, the density to be 1.00×103kg/m3, and the surface area to be πr2
42. Using Stokes’ law, verify that the units for viscosity are kilograms per meter per second.
Solution
[η]=[Fs][r][v]=kg⋅m/s2m⋅m/s=kgm⋅s
43. Find the terminal velocity of a spherical bacterium (diameter 2.00μm falling in water. You will first need to note that the drag force is equal to the weight at terminal velocity. Take the density of the bacterium to be 1.10×103kg/m3.
44. Stokes’ law describes sedimentation of particles in liquids and can be used to measure viscosity. Particles in liquids achieve terminal velocity quickly. One can measure the time it takes for a particle to fall a certain distance and then use Stokes’ law to calculate the viscosity of the liquid. Suppose a steel ball bearing (density 7.8×103kg/m3, diameter 3.0mm) is dropped in a container of motor oil. It takes 12 s to fall a distance of 0.60 m. Calculate the viscosity of the oil.
Solution
0.76kg/m⋅s
5.3: Elasticity: Stress and Strain
45. During a circus act, one performer swings upside down hanging from a trapeze holding another, also upside-down, performer by the legs. If the upward force on the lower performer is three times her weight, how much do the bones (the femurs) in her upper legs stretch? You may assume each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius. Her mass is 60.0 kg.
Solution
1.90×10−3cm
46. During a wrestling match, a 150 kg wrestler briefly stands on one hand during a maneuver designed to perplex his already moribund adversary. By how much does the upper arm bone shorten in length? The bone can be represented by a uniform rod 38.0 cm in length and 2.10 cm in radius.
47. (a) The “lead” in pencils is a graphite composition with a Young’s modulus of about 1×109N/m2. Calculate the change in length of the lead in an automatic pencil if you tap it straight into the pencil with a force of 4.0 N. The lead is 0.50 mm in diameter and 60 mm long. (b) Is the answer reasonable? That is, does it seem to be consistent with what you have observed when using pencils?
Solution
(a)1 mm
(b) This does seem reasonable, since the lead does seem to shrink a little when you push on it.
48. TV broadcast antennas are the tallest artificial structures on Earth. In 1987, a 72.0-kg physicist placed himself and 400 kg of equipment at the top of one 610-m high antenna to perform gravity experiments. By how much was the antenna compressed, if we consider it to be equivalent to a steel cylinder 0.150 m in radius?
49. (a) By how much does a 65.0-kg mountain climber stretch her 0.800-cm diameter nylon rope when she hangs 35.0 m below a rock outcropping? (b) Does the answer seem to be consistent with what you have observed for nylon ropes? Would it make sense if the rope were actually a bungee cord?
Solution
(a)9 cm
(b)This seems reasonable for nylon climbing rope, since it is not supposed to stretch that much.
50. A 20.0-m tall hollow aluminum flagpole is equivalent in stiffness to a solid cylinder 4.00 cm in diameter. A strong wind bends the pole much as a horizontal force of 900 N exerted at the top would. How far to the side does the top of the pole flex?
51. As an oil well is drilled, each new section of drill pipe supports its own weight and that of the pipe and drill bit beneath it. Calculate the stretch in a new 6.00 m length of steel pipe that supports 3.00 km of pipe having a mass of 20.0 kg/m and a 100-kg drill bit. The pipe is equivalent in stiffness to a solid cylinder 5.00 cm in diameter.
Solution
8.59 mm
52. Calculate the force a piano tuner applies to stretch a steel piano wire 8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.
53. A vertebra is subjected to a shearing force of 500 N. Find the shear deformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00 cm in diameter.
Solution
1.49×10−7m
54. A disk between vertebrae in the spine is subjected to a shearing force of 600 N. Find its shear deformation, taking it to have the shear modulus of 1×109N/m2. The disk is equivalent to a solid cylinder 0.700 cm high and 4.00 cm in diameter.
55. When using a pencil eraser, you exert a vertical force of 6.00 N at a distance of 2.00 cm from the hardwood-eraser joint. The pencil is 6.00 mm in diameter and is held at an angle of 20.0º to the horizontal.
(a) By how much does the wood flex perpendicular to its length?
(b) How much is it compressed lengthwise?
Solution
(a) 3.99×10−7m
(b) 9.67×10−8m
56. To consider the effect of wires hung on poles, we take data from [link], in which tensions in wires supporting a traffic light were calculated. The left wire made an angle 30.0º below the horizontal with the top of its pole and carried a tension of 108 N. The 12.0 m tall hollow aluminum pole is equivalent in stiffness to a 4.50 cm diameter solid cylinder. (a) How far is it bent to the side? (b) By how much is it compressed?
57. A farmer making grape juice fills a glass bottle to the brim and caps it tightly. The juice expands more than the glass when it warms up, in such a way that the volume increases by 0.2% (that is, ΔV/V0=2×10−3) relative to the space available. Calculate the magnitude of the normal force exerted by the juice per square centimeter if its bulk modulus is 1.8×109N/m2, assuming the bottle does not break. In view of your answer, do you think the bottle will survive?
Solution
4×106N/m2. This is about 36 atm, greater than a typical jar can withstand.
58. (a) When water freezes, its volume increases by 9.05% (that is, ΔV/V0=9.05×10−2). What force per unit area is water capable of exerting on a container when it freezes? (It is acceptable to use the bulk modulus of water in this problem.)
(b) Is it surprising that such forces can fracture engine blocks, boulders, and the like?
59. This problem returns to the tightrope walker studied in [link], who created a tension of 3.94×103N in a wire making an angle 5.0º below the horizontal with each supporting pole. Calculate how much this tension stretches the steel wire if it was originally 15 m long and 0.50 cm in diameter.
Solution
1.4 cm
60. The pole in Figure is at a 90.0º bend in a power line and is therefore subjected to more shear force than poles in straight parts of the line. The tension in each line is 4.00×104N, at the angles shown. The pole is 15.0 m tall, has an 18.0 cm diameter, and can be considered to have half the stiffness of hardwood.
(a) Calculate the compression of the pole.
(b) Find how much it bends and in what direction.
(c) Find the tension in a guy wire used to keep the pole straight if it is attached to the top of the pole at an angle of 30.0º with the vertical. (Clearly, the guy wire must be in the opposite direction of the bend.)
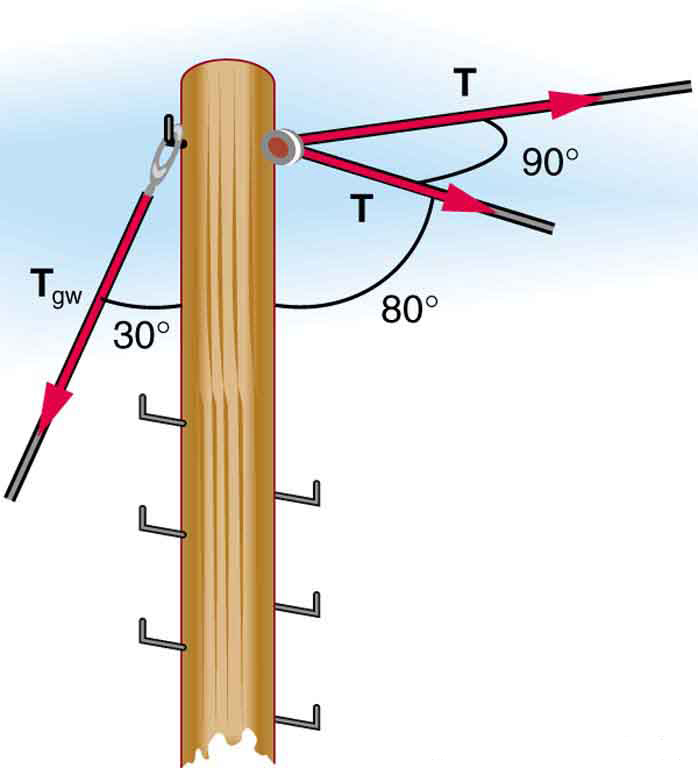
This telephone pole is at a 90º bend in a power line. A guy wire is attached to the top of the pole at an angle of 30º with the vertical.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


