20.E: Heat and Heat Transfer Methods (Exercise)
- Last updated
- Save as PDF
- Page ID
- 15419
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
20.1: Current
1. Can a wire carry a current and still be neutral—that is, have a total charge of zero? Explain.
2. Car batteries are rated in ampere-hours (A⋅h). To what physical quantity do ampere-hours correspond (voltage, charge, . . .), and what relationship do ampere-hours have to energy content?
3. If two different wires having identical cross-sectional areas carry the same current, will the drift velocity be higher or lower in the better conductor? Explain in terms of the equation \(\displaystyle v_d=\frac{I}{nqA}\), by considering how the density of charge carriers \(\displaystyle n\) relates to whether or not a material is a good conductor.
4. Why are two conducting paths from a voltage source to an electrical device needed to operate the device?
5. In cars, one battery terminal is connected to the metal body. How does this allow a single wire to supply current to electrical devices rather than two wires?
6. Why isn’t a bird sitting on a high-voltage power line electrocuted? Contrast this with the situation in which a large bird hits two wires simultaneously with its wings.
20.2: Ohm’s Law: Resistance and Simple Circuits
7. The \(\displaystyle IR\) drop across a resistor means that there is a change in potential or voltage across the resistor. Is there any change in current as it passes through a resistor? Explain.
8. How is the \(\displaystyle IR\) drop in a resistor similar to the pressure drop in a fluid flowing through a pipe?
20.3: Resistance and Resistivity
9. In which of the three semiconducting materials listed in Table do impurities supply free charges? (Hint: Examine the range of resistivity for each and determine whether the pure semiconductor has the higher or lower conductivity.)
10. Does the resistance of an object depend on the path current takes through it? Consider, for example, a rectangular bar—is its resistance the same along its length as across its width? (See Figure.)
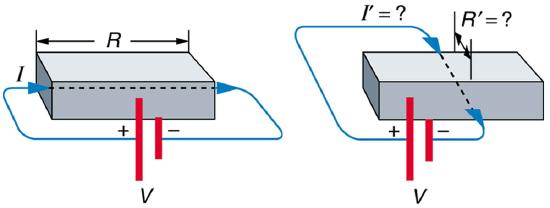
Does current taking two different paths through the same object encounter different resistance?
11. If aluminum and copper wires of the same length have the same resistance, which has the larger diameter? Why?
12. Explain why \(\displaystyle R=R_0(1+αΔT)\) for the temperature variation of the resistance \(\displaystyle R\) of an object is not as accurate as \(\displaystyle ρ=ρ_0(1+αΔT)\), which gives the temperature variation of resistivity ρ size 12{ρ} {}.
20.4: Electric Power and Energy
13. Why do incandescent lightbulbs grow dim late in their lives, particularly just before their filaments break?
14. The power dissipated in a resistor is given by \(\displaystyle P=V^2/R\), which means power decreases if resistance increases. Yet this power is also given by \(\displaystyle P=I^2R\), which means power increases if resistance increases. Explain why there is no contradiction here.
20.5: Alternating Current versus Direct Current
15. Give an example of a use of AC power other than in the household. Similarly, give an example of a use of DC power other than that supplied by batteries.
16. Why do voltage, current, and power go through zero 120 times per second for 60-Hz AC electricity?
17. You are riding in a train, gazing into the distance through its window. As close objects streak by, you notice that the nearby fluorescent lights make dashed streaks. Explain.
20.6: Electric Hazards and the Human Body
18. Using an ohmmeter, a student measures the resistance between various points on his body. He finds that the resistance between two points on the same finger is about the same as the resistance between two points on opposite hands—both are several hundred thousand ohms. Furthermore, the resistance decreases when more skin is brought into contact with the probes of the ohmmeter. Finally, there is a dramatic drop in resistance (to a few thousand ohms) when the skin is wet. Explain these observations and their implications regarding skin and internal resistance of the human body.
19. What are the two major hazards of electricity?
20. Why isn’t a short circuit a shock hazard?
21. What determines the severity of a shock? Can you say that a certain voltage is hazardous without further information?
22. An electrified needle is used to burn off warts, with the circuit being completed by having the patient sit on a large butt plate. Why is this plate large?
23. Some surgery is performed with high-voltage electricity passing from a metal scalpel through the tissue being cut. Considering the nature of electric fields at the surface of conductors, why would you expect most of the current to flow from the sharp edge of the scalpel? Do you think high- or low-frequency AC is used?
24. Some devices often used in bathrooms, such as hairdryers, often have safety messages saying “Do not use when the bathtub or basin is full of water.” Why is this so?
25. We are often advised to not flick electric switches with wet hands, dry your hand first. We are also advised to never throw water on an electric fire. Why is this so?
26. Before working on a power transmission line, linemen will touch the line with the back of the hand as a final check that the voltage is zero. Why the back of the hand?
27. Why is the resistance of wet skin so much smaller than dry, and why do blood and other bodily fluids have low resistances?
28. Could a person on intravenous infusion (an IV) be microshock sensitive?
29. In view of the small currents that cause shock hazards and the larger currents that circuit breakers and fuses interrupt, how do they play a role in preventing shock hazards?
20.7: Nerve Conduction–Electrocardiograms
30. Note that in Figure, both the concentration gradient and the Coulomb force tend to move \(\displaystyle Na^+\) ions into the cell. What prevents this?
31. Define depolarization, repolarization, and the action potential.
32. Explain the properties of myelinated nerves in terms of the insulating properties of myelin.
Problems & Exercises
20.1: Current
33. What is the current in milliamperes produced by the solar cells of a pocket calculator through which 4.00 C of charge passes in 4.00 h?
Solution
0.278 mA
34. A total of 600 C of charge passes through a flashlight in 0.500 h. What is the average current?
35. What is the current when a typical static charge of \(\displaystyle 0.250μC\) moves from your finger to a metal doorknob in \(\displaystyle 1.00μs\)?
Solution
0.250 A
36. Find the current when 2.00 nC jumps between your comb and hair over a \(\displaystyle 0.500 -μs\) time interval.
37. A large lightning bolt had a 20,000-A current and moved 30.0 C of charge. What was its duration?
Solution
1.50ms
38. The 200-A current through a spark plug moves 0.300 mC of charge. How long does the spark last?
39. (a) A defibrillator sends a 6.00-A current through the chest of a patient by applying a 10,000-V potential as in the figure below. What is the resistance of the path? (b) The defibrillator paddles make contact with the patient through a conducting gel that greatly reduces the path resistance. Discuss the difficulties that would ensue if a larger voltage were used to produce the same current through the patient, but with the path having perhaps 50 times the resistance. (Hint: The current must be about the same, so a higher voltage would imply greater power. Use this equation for power: \(\displaystyle P=I^2R\).)
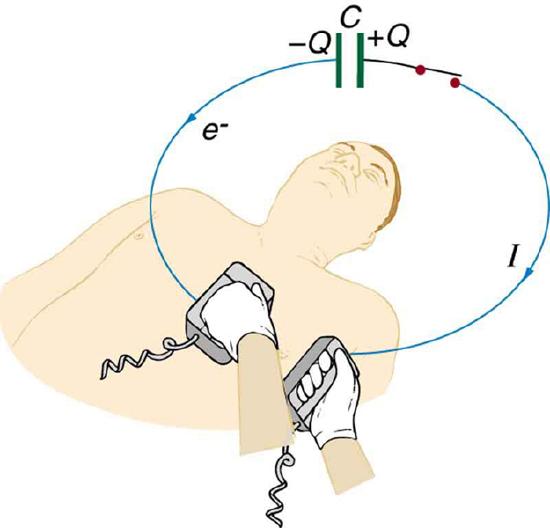
The capacitor in a defibrillation unit drives a current through the heart of a patient.
Solution
(a) \(\displaystyle 1.67kΩ\)
(b) If a 50 times larger resistance existed, keeping the current about the same, the power would be increased by a factor of about 50 (based on the equation \(\displaystyle P=I^2R\)), causing much more energy to be transferred to the skin, which could cause serious burns. The gel used reduces the resistance, and therefore reduces the power transferred to the skin.
40. During open-heart surgery, a defibrillator can be used to bring a patient out of cardiac arrest. The resistance of the path is \(\displaystyle 500 Ω\) and a 10.0-mA current is needed. What voltage should be applied?
41. (a) A defibrillator passes 12.0 A of current through the torso of a person for 0.0100 s. How much charge moves?
(b) How many electrons pass through the wires connected to the patient? (See figure two problems earlier.)
Solution
(a) 0.120 C
(b) \(\displaystyle 7.50×10^{17}electrons\)
42. A clock battery wears out after moving 10,000 C of charge through the clock at a rate of 0.500 mA.
(a) How long did the clock run?
(b) How many electrons per second flowed?
43. The batteries of a submerged non-nuclear submarine supply 1000 A at full speed ahead. How long does it take to move Avogadro’s number (\(\displaystyle 6.02×10^{23}\)) of electrons at this rate?
Solution
96.3 s
44. Electron guns are used in X-ray tubes. The electrons are accelerated through a relatively large voltage and directed onto a metal target, producing X-rays.
(a) How many electrons per second strike the target if the current is 0.500 mA?
(b) What charge strikes the target in 0.750 s?
45. A large cyclotron directs a beam of \(\displaystyle He^{++}\) nuclei onto a target with a beam current of 0.250 mA.
(a) How many \(\displaystyle He^{++}\) nuclei per second is this?
(b) How long does it take for 1.00 C to strike the target?
(c) How long before 1.00 mol of \(\displaystyle He^{++}\) nuclei strike the target?
Solution
(a) \(\displaystyle 7.81 × 10^{14}He^{++}nuclei/s\)
(b) \(\displaystyle 4.00 × 10^3s\)
(c) \(\displaystyle 7.71 × 10^8s\)
46. Repeat the above example on Example, but for a wire made of silver and given there is one free electron per silver atom.
47. Using the results of the above example on Example, find the drift velocity in a copper wire of twice the diameter and carrying 20.0 A.
Solution
\(\displaystyle −1.13×10^{−4}m/s\)
48. A 14-gauge copper wire has a diameter of 1.628 mm. What magnitude current flows when the drift velocity is 1.00 mm/s? (See above example on Example for useful information.)
49. SPEAR, a storage ring about 72.0 m in diameter at the Stanford Linear Accelerator (closed in 2009), has a 20.0-A circulating beam of electrons that are moving at nearly the speed of light. (See Figure.) How many electrons are in the beam?
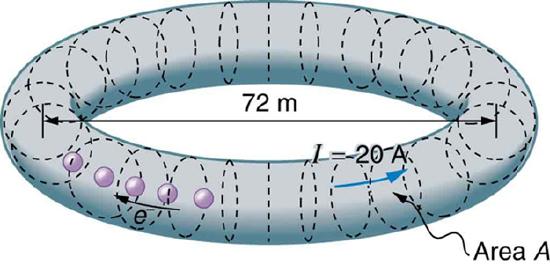
Electrons circulating in the storage ring called SPEAR constitute a 20.0-A current. Because they travel close to the speed of light, each electron completes many orbits in each second.
Solution
\(\displaystyle 9.42×10^{13}electrons\)
20.2: Ohm’s Law: Resistance and Simple Circuits
50. What current flows through the bulb of a 3.00-V flashlight when its hot resistance is \(\displaystyle 3.60 Ω\)?
Solution
0.833 A
51. Calculate the effective resistance of a pocket calculator that has a 1.35-V battery and through which 0.200 mA flows.
52. What is the effective resistance of a car’s starter motor when 150 A flows through it as the car battery applies 11.0 V to the motor?
Solution
\(\displaystyle 7.33×10^{−2}Ω\)
53. How many volts are supplied to operate an indicator light on a DVD player that has a resistance of \(\displaystyle 140Ω\), given that 25.0 mA passes through it?
54. (a) Find the voltage drop in an extension cord having a \(\displaystyle 0.0600-Ω\) resistance and through which 5.00 A is flowing.
(b) A cheaper cord utilizes thinner wire and has a resistance of \(\displaystyle 0.300Ω\). What is the voltage drop in it when 5.00 A flows?
(c) Why is the voltage to whatever appliance is being used reduced by this amount? What is the effect on the appliance?
Solution
(a) 0.300 V
(b) 1.50 V
(c) The voltage supplied to whatever appliance is being used is reduced because the total voltage drop from the wall to the final output of the appliance is fixed. Thus, if the voltage drop across the extension cord is large, the voltage drop across the appliance is significantly decreased, so the power output by the appliance can be significantly decreased, reducing the ability of the appliance to work properly.
55. A power transmission line is hung from metal towers with glass insulators having a resistance of \(\displaystyle 1.00×10^9Ω\). What current flows through the insulator if the voltage is 200 kV? (Some high-voltage lines are DC.)
20.3: Resistance and Resistivity
56. What is the resistance of a 20.0-m-long piece of 12-gauge copper wire having a 2.053-mm diameter?
Solution
0.104 Ω
57. The diameter of 0-gauge copper wire is 8.252 mm. Find the resistance of a 1.00-km length of such wire used for power transmission.
58. If the 0.100-mm diameter tungsten filament in a light bulb is to have a resistance of \(\displaystyle 0.200 Ω\) at \(\displaystyle 20.0ºC\), how long should it be?
Solution
\(\displaystyle 2.8×10^{−2}m\)
59. Find the ratio of the diameter of aluminum to copper wire, if they have the same resistance per unit length (as they might in household wiring).
60. What current flows through a 2.54-cm-diameter rod of pure silicon that is 20.0 cm long, when \(\displaystyle 1.00 × 10^3V\) is applied to it? (Such a rod may be used to make nuclear-particle detectors, for example.)
Solution
\(\displaystyle 1.10×10^{−3}A\)
61. (a) To what temperature must you raise a copper wire, originally at \(\displaystyle 20.0ºC\), to double its resistance, neglecting any changes in dimensions?
(b) Does this happen in household wiring under ordinary circumstances?
62. A resistor made of Nichrome wire is used in an application where its resistance cannot change more than 1.00% from its value at \(\displaystyle 20.0ºC\). Over what temperature range can it be used?
Solution
\(\displaystyle −5ºC\) to \(\displaystyle 45ºC\)
63. Of what material is a resistor made if its resistance is 40.0% greater at \(\displaystyle 100ºC\) than at \(\displaystyle 20.0ºC\)?
64. An electronic device designed to operate at any temperature in the range from \(\displaystyle –10.0ºC\) to \(\displaystyle 55.0ºC\) contains pure carbon resistors. By what factor does their resistance increase over this range?
Solution
1.03
65. (a) Of what material is a wire made, if it is 25.0 m long with a 0.100 mm diameter and has a resistance of \(\displaystyle 77.7Ω\) at \(\displaystyle 20.0ºC\)?
(b) What is its resistance at \(\displaystyle 150ºC\)?
66. Assuming a constant temperature coefficient of resistivity, what is the maximum percent decrease in the resistance of a constantan wire starting at \(\displaystyle 20.0ºC\)?
Solution
0.06%
67. A wire is drawn through a die, stretching it to four times its original length. By what factor does its resistance increase?
68. A copper wire has a resistance of \(\displaystyle 0.500Ω\) at \(\displaystyle 20.0ºC\), and an iron wire has a resistance of \(\displaystyle 0.525Ω\) at the same temperature. At what temperature are their resistance equal?
Solution
\(\displaystyle −17ºC\)
69. (a) Digital medical thermometers determine temperature by measuring the resistance of a semiconductor device called a thermistor (which has \(\displaystyle α=–0.0600/ºC\)) when it is at the same temperature as the patient. What is a patient’s temperature if the thermistor’s resistance at that temperature is 82.0% of its value at \(\displaystyle 37.0ºC\) (normal body temperature)?
(b) The negative value for α size 12{α} {} may not be maintained for very low temperatures. Discuss why and whether this is the case here. (Hint: Resistance can’t become negative.)
70. Integrated Concepts
(a) Redo Exercise taking into account the thermal expansion of the tungsten filament. You may assume a thermal expansion coefficient of \(\displaystyle 12×10^{−6}/ºC\).
(b) By what percentage does your answer differ from that in the example?
Solution
(a) \(\displaystyle 4.7Ω\) (total)
(b) 3.0% decrease
71. Unreasonable Results
(a) To what temperature must you raise a resistor made of constantan to double its resistance, assuming a constant temperature coefficient of resistivity?
(b) To cut it in half?
(c) What is unreasonable about these results? (d) Which assumptions are unreasonable, or which premises are inconsistent?
20.4: Electric Power and Energy
72. What is the power of a \(\displaystyle 1.00×10^2MV\) lightning bolt having a current of \(\displaystyle 2.00 × 10^4A\)?
Solution
\(\displaystyle 2.00×10^{12}W\)
73. What power is supplied to the starter motor of a large truck that draws 250 A of current from a 24.0-V battery hookup?
74. A charge of 4.00 C of charge passes through a pocket calculator’s solar cells in 4.00 h. What is the power output, given the calculator’s voltage output is 3.00 V? (See Figure.)

The strip of solar cells just above the keys of this calculator convert light to electricity to supply its energy needs. (credit: Evan-Amos, Wikimedia Commons)
75. How many watts does a flashlight that has \(\displaystyle 6.00×10^2C\) pass through it in 0.500 h use if its voltage is 3.00 V?
76. Find the power dissipated in each of these extension cords:
(a) an extension cord having a \(\displaystyle 0.0600-Ω\) resistance and through which 5.00 A is flowing;
(b) a cheaper cord utilizing thinner wire and with a resistance of \(\displaystyle 0.300Ω.\)
Solution
(a) 1.50 W
(b) 7.50 W
77. Verify that the units of a volt-ampere are watts, as implied by the equation \(\displaystyle P=IV\).
78. Show that the units \(\displaystyle 1V^2/Ω=1W \), as implied by the equation \(\displaystyle P=V^2/R\).
Solution
\(\displaystyle \frac{V^2}{Ω}=\frac{V^2}{V/A}=AV=(\frac{C}{s})(\frac{J}{C})=\frac{J}{s}=1W\)
79. Show that the units \(\displaystyle 1A^2⋅Ω=1W\), as implied by the equation \(\displaystyle P=I^2R\).
80. Verify the energy unit equivalence that \(\displaystyle 1kW⋅h = 3.60×10^6J\).
Solution
\(\displaystyle 1kW⋅h=(\frac{1×10^3J}{1 s})(1 h)(\frac{3600s}{1h})=3.60×10^6J\)
81. Electrons in an X-ray tube are accelerated through \(\displaystyle 1.00×10^2kV\) and directed toward a target to produce X-rays. Calculate the power of the electron beam in this tube if it has a current of 15.0 mA.
82. An electric water heater consumes 5.00 kW for 2.00 h per day. What is the cost of running it for one year if electricity costs \(\displaystyle 12.0 cents/kW⋅h\)? See Figure.

On-demand electric hot water heater. Heat is supplied to water only when needed. (credit: aviddavid, Flickr)
Solution
$438/y
83. With a 1200-W toaster, how much electrical energy is needed to make a slice of toast (cooking time = 1 minute)? At \(\displaystyle 9.0 cents/kW ⋅ h\) , how much does this cost?
84. What would be the maximum cost of a CFL such that the total cost (investment plus operating) would be the same for both CFL and incandescent 60-W bulbs? Assume the cost of the incandescent bulb is 25 cents and that electricity costs \(\displaystyle 10 cents/kWh\). Calculate the cost for 1000 hours, as in the cost effectiveness of CFL example.
Solution
$6.25
85. Some makes of older cars have 6.00-V electrical systems.
(a) What is the hot resistance of a 30.0-W headlight in such a car?
(b) What current flows through it?
86. Alkaline batteries have the advantage of putting out constant voltage until very nearly the end of their life. How long will an alkaline battery rated at \(\displaystyle 1.00 A⋅h\) and 1.58 V keep a 1.00-W flashlight bulb burning?
Solution
1.58 h
87. A cauterizer, used to stop bleeding in surgery, puts out 2.00 mA at 15.0 kV.
(a) What is its power output?
(b) What is the resistance of the path?
88. The average television is said to be on 6 hours per day. Estimate the yearly cost of electricity to operate 100 million TVs, assuming their power consumption averages 150 W and the cost of electricity averages \(\displaystyle 12.0cents/kW⋅h\).
Solution
$3.94 billion/year
89. An old lightbulb draws only 50.0 W, rather than its original 60.0 W, due to evaporative thinning of its filament. By what factor is its diameter reduced, assuming uniform thinning along its length? Neglect any effects caused by temperature differences.
90. 00-gauge copper wire has a diameter of 9.266 mm. Calculate the power loss in a kilometer of such wire when it carries \(\displaystyle 1.00×10^2A\).
Solution
25.5 W
91. Integrated Concepts
Cold vaporizers pass a current through water, evaporating it with only a small increase in temperature. One such home device is rated at 3.50 A and utilizes 120 V AC with 95.0% efficiency.
(a) What is the vaporization rate in grams per minute?
(b) How much water must you put into the vaporizer for 8.00 h of overnight operation? (See Figure.)
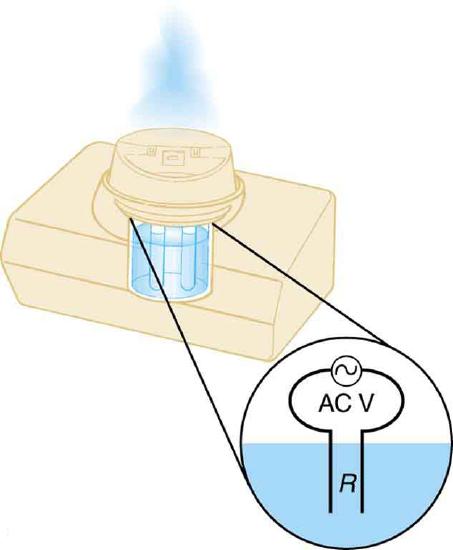
This cold vaporizer passes current directly through water, vaporizing it directly with relatively little temperature increase.
92. Integrated Concepts
(a) What energy is dissipated by a lightning bolt having a 20,000-A current, a voltage of \(\displaystyle 1.00×10^2MV\), and a length of 1.00 ms?
(b) What mass of tree sap could be raised from \(\displaystyle 18.0ºC\) to its boiling point and then evaporated by this energy, assuming sap has the same thermal characteristics as water?
Solution
(a) \(\displaystyle 2.00×10^9J\)
(b) 769 kg
93. Integrated Concepts
What current must be produced by a 12.0-V battery-operated bottle warmer in order to heat 75.0 g of glass, 250 g of baby formula, and \(\displaystyle 3.00×10^2g\) of aluminum from \(\displaystyle 20.0ºC\) to \(\displaystyle 90.0ºC\) in 5.00 min?
94. Integrated Concepts
How much time is needed for a surgical cauterizer to raise the temperature of 1.00 g of tissue from \(\displaystyle 37.0ºC\) to \(\displaystyle 100ºC\) and then boil away 0.500 g of water, if it puts out 2.00 mA at 15.0 kV? Ignore heat transfer to the surroundings.
Solution
45.0 s
95. Integrated Concepts
Hydroelectric generators (see Figure) at Hoover Dam produce a maximum current of \(\displaystyle 8.00×10^3A\) at 250 kV.
(a) What is the power output?
(b) The water that powers the generators enters and leaves the system at low speed (thus its kinetic energy does not change) but loses 160 m in altitude. How many cubic meters per second are needed, assuming 85.0% efficiency?

Hydroelectric generators at the Hoover dam. (credit: Jon Sullivan)
96. Integrated Concepts
Assuming 95.0% efficiency for the conversion of electrical power by the motor, what current must the 12.0-V batteries of a 750-kg electric car be able to supply:
(a) To accelerate from rest to 25.0 m/s in 1.00 min?
(b) To climb a \(\displaystyle 2.00×10^2-m\)-high hill in 2.00 min at a constant 25.0-m/s speed while exerting \(\displaystyle 5.00×10^2N\) of force to overcome air resistance and friction?
(c) To travel at a constant 25.0-m/s speed, exerting a \(\displaystyle 5.00×10^2N\) force to overcome air resistance and friction? See Figure.

This REVAi, an electric car, gets recharged on a street in London. (credit: Frank Hebbert)
Solution
(a) 343 A
(b) \(\displaystyle 2.17×10^3A\)
(c) \(\displaystyle 1.10×10^3A\)
97. Integrated Concepts
A light-rail commuter train draws 630 A of 650-V DC electricity when accelerating.
(a) What is its power consumption rate in kilowatts?
(b) How long does it take to reach 20.0 m/s starting from rest if its loaded mass is \(\displaystyle 5.30×10^4kg\), assuming 95.0% efficiency and constant power?
(c) Find its average acceleration.
(d) Discuss how the acceleration you found for the light-rail train compares to what might be typical for an automobile.
98. Integrated Concepts
(a) An aluminum power transmission line has a resistance of \(\displaystyle 0.0580Ω/km\). What is its mass per kilometer?
(b) What is the mass per kilometer of a copper line having the same resistance? A lower resistance would shorten the heating time. Discuss the practical limits to speeding the heating by lowering the resistance.
Solution
(a) \(\displaystyle 1.23×10^3kg\)
(b) \(\displaystyle 2.64×10^3kg\)
99. Integrated Concepts
(a) An immersion heater utilizing 120 V can raise the temperature of a \(\displaystyle 1.00×10^2\)-g aluminum cup containing 350 g of water from \(\displaystyle 20.0ºC\) to \(\displaystyle 95.0ºC\) in 2.00 min. Find its resistance, assuming it is constant during the process.
(b) A lower resistance would shorten the heating time. Discuss the practical limits to speeding the heating by lowering the resistance.
100. Integrated Concepts
(a) What is the cost of heating a hot tub containing 1500 kg of water from \(\displaystyle 10.0ºC\) to \(\displaystyle 40.0ºC\), assuming 75.0% efficiency to account for heat transfer to the surroundings? The cost of electricity is \(\displaystyle 9cents/kW⋅h\).
(b) What current was used by the 220-V AC electric heater, if this took 4.00 h?
101. Unreasonable Results
(a) What current is needed to transmit \(\displaystyle 1.00×10^2MW\) of power at 480 V?
(b) What power is dissipated by the transmission lines if they have a \(\displaystyle 1.00-Ω\) resistance?
(c) What is unreasonable about this result?
(d) Which assumptions are unreasonable, or which premises are inconsistent?
Solution
(a) \(\displaystyle 2.08×10^5A\)
(b) \(\displaystyle 4.33×10^4MW\)
(c) The transmission lines dissipate more power than they are supposed to transmit.
(d) A voltage of 480 V is unreasonably low for a transmission voltage. Long-distance transmission lines are kept at much higher voltages (often hundreds of kilovolts) to reduce power losses.
102. Unreasonable Results
(a) What current is needed to transmit \(\displaystyle 1.00×10^2MW\) of power at 10.0 kV?
(b) Find the resistance of 1.00 km of wire that would cause a 0.0100% power loss.
(c) What is the diameter of a 1.00-km-long copper wire having this resistance?
(d) What is unreasonable about these results?
(e) Which assumptions are unreasonable, or which premises are inconsistent?
103. Construct Your Own Problem
Consider an electric immersion heater used to heat a cup of water to make tea. Construct a problem in which you calculate the needed resistance of the heater so that it increases the temperature of the water and cup in a reasonable amount of time. Also calculate the cost of the electrical energy used in your process. Among the things to be considered are the voltage used, the masses and heat capacities involved, heat losses, and the time over which the heating takes place. Your instructor may wish for you to consider a thermal safety switch (perhaps bimetallic) that will halt the process before damaging temperatures are reached in the immersion unit.
20.5: Alternating Current versus Direct Current
104. (a) What is the hot resistance of a 25-W light bulb that runs on 120-V AC?
(b) If the bulb’s operating temperature is \(\displaystyle 2700ºC\), what is its resistance at \(\displaystyle 2600ºC\)`?
105. Certain heavy industrial equipment uses AC power that has a peak voltage of 679 V. What is the rms voltage?
Solution
480 V
106. A certain circuit breaker trips when the rms current is 15.0 A. What is the corresponding peak current?
107. Military aircraft use 400-Hz AC power, because it is possible to design lighter-weight equipment at this higher frequency. What is the time for one complete cycle of this power?
Solution
2.50 ms
108. A North American tourist takes his 25.0-W, 120-V AC razor to Europe, finds a special adapter, and plugs it into 240 V AC. Assuming constant resistance, what power does the razor consume as it is ruined?
109. In this problem, you will verify statements made at the end of the power losses for Example. (a) What current is needed to transmit 100 MW of power at a voltage of 25.0 kV? (b) Find the power loss in a 1.00 -Ω size 12{1 "." "00"- %OMEGA } {} transmission line. (c) What percent loss does this represent?
Solution
(a) 4.00 kA
(b) 16.0 MW
(c) 16.0%
110. A small office-building air conditioner operates on 408-V AC and consumes 50.0 kW.
(a) What is its effective resistance?
(b) What is the cost of running the air conditioner during a hot summer month when it is on 8.00 h per day for 30 days and electricity costs \(\displaystyle 9.00 cents/kW⋅h\)?
111. What is the peak power consumption of a 120-V AC microwave oven that draws 10.0 A?
Solution
2.40 kW
112. What is the peak current through a 500-W room heater that operates on 120-V AC power?
113. Two different electrical devices have the same power consumption, but one is meant to be operated on 120-V AC and the other on 240-V AC.
(a) What is the ratio of their resistances?
(b) What is the ratio of their currents?
(c) Assuming its resistance is unaffected, by what factor will the power increase if a 120-V AC device is connected to 240-V AC?
Solution
(a) 4.0
(b) 0.50
(c) 4.0
114. Nichrome wire is used in some radiative heaters.
(a) Find the resistance needed if the average power output is to be 1.00 kW utilizing 120-V AC.
(b) What length of Nichrome wire, having a cross-sectional area of \(\displaystyle 5.00mm^2\), is needed if the operating temperature is \(\displaystyle 500º C\)?
(c) What power will it draw when first switched on?
115. Find the time after \(\displaystyle t=0\) when the instantaneous voltage of 60-Hz AC first reaches the following values:
(a) \(\displaystyle V_0/2\)
(b) \(\displaystyle V_0\)
(c) 0.
Solution
(a) 1.39 ms
(b) 4.17 ms
(c) 8.33 ms
116. (a) At what two times in the first period following \(\displaystyle t=0\) does the instantaneous voltage in 60-Hz AC equal \(\displaystyle V_{rms}\)?
(b) \(\displaystyle −V_{rms}\)?
20.6: Electric Hazards and the Human Body
117. (a) How much power is dissipated in a short circuit of 240-V AC through a resistance of \(\displaystyle 0.250Ω\)?
(b) What current flows?
Solution
(a) 230 kW
(b) 960 A
118. What voltage is involved in a 1.44-kW short circuit through a \(\displaystyle 0.100-Ω\) resistance?
119. Find the current through a person and identify the likely effect on her if she touches a 120-V AC source
(a) if she is standing on a rubber mat and offers a total resistance of \(\displaystyle 300 kΩ\);
(b) if she is standing barefoot on wet grass and has a resistance of only \(\displaystyle 4000 kΩ\).
Solution
(a) 0.400 mA, no effect
(b) 26.7 mA, muscular contraction for duration of the shock (can't let go)
120. While taking a bath, a person touches the metal case of a radio. The path through the person to the drainpipe and ground has a resistance of \(\displaystyle 4000Ω\). What is the smallest voltage on the case of the radio that could cause ventricular fibrillation?
121. Foolishly trying to fish a burning piece of bread from a toaster with a metal butter knife, a man comes into contact with 120-V AC. He does not even feel it since, luckily, he is wearing rubber-soled shoes. What is the minimum resistance of the path the current follows through the person?
Solution
\(\displaystyle 1.20×10^5Ω\)
122. (a) During surgery, a current as small as \(\displaystyle 20.0 μA\) applied directly to the heart may cause ventricular fibrillation. If the resistance of the exposed heart is \(\displaystyle 300Ω\), what is the smallest voltage that poses this danger?
(b) Does your answer imply that special electrical safety precautions are needed?
123. (a) What is the resistance of a 220-V AC short circuit that generates a peak power of 96.8 kW?
(b) What would the average power be if the voltage was 120 V AC?
Solution
(a) \(\displaystyle 1.00Ω\)
(b) 14.4 kW
124. A heart defibrillator passes 10.0 A through a patient’s torso for 5.00 ms in an attempt to restore normal beating.
(a) How much charge passed?
(b) What voltage was applied if 500 J of energy was dissipated?
(c) What was the path’s resistance?
(d) Find the temperature increase caused in the 8.00 kg of affected tissue.
125. Integrated Concepts
A short circuit in a 120-V appliance cord has a \(\displaystyle 0.500-Ω\) resistance. Calculate the temperature rise of the 2.00 g of surrounding materials, assuming their specific heat capacity is \(\displaystyle 0.200cal/g⋅ºC\) and that it takes 0.0500 s for a circuit breaker to interrupt the current. Is this likely to be damaging?
Solution
Temperature increases \(\displaystyle 860º C\) . It is very likely to be damaging.
126. Construct Your Own Problem
Consider a person working in an environment where electric currents might pass through her body. Construct a problem in which you calculate the resistance of insulation needed to protect the person from harm. Among the things to be considered are the voltage to which the person might be exposed, likely body resistance (dry, wet, …), and acceptable currents (safe but sensed, safe and unfelt, …).
20.7: Nerve Conduction–Electrocardiograms
127. Integrated Concepts
Use the ECG in Figure to determine the heart rate in beats per minute assuming a constant time between beats.
Solution
80 beats/minute
128. Integrated Concepts
(a) Referring to Figure, find the time systolic pressure lags behind the middle of the QRS complex.
(b) Discuss the reasons for the time lag.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

