5.1: Angular Momentum In Two Dimensions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Sure, and maybe the sun won't come up tomorrow.” Of course, the sun only appears to go up and down because the earth spins, so the cliche should really refer to the unlikelihood of the earth's stopping its rotation abruptly during the night. Why can't it stop? It wouldn't violate conservation of momentum, because the earth's rotation doesn't add anything to its momentum. While California spins in one direction, some equally massive part of India goes the opposite way, canceling its momentum. A halt to Earth's rotation would entail a drop in kinetic energy, but that energy could simply be converted into some other form, such as heat.

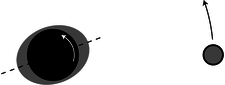
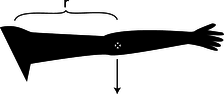
a / The jumper can't move his legs counterclockwise without moving his arms clockwise. (Thomas Eakins.)
Other examples along these lines are not hard to find. An atom spins at the same rate for billions of years. A high-diver who is rotating when he comes off the board does not need to make any physical effort to continue rotating, and indeed would be unable to stop rotating before he hit the water.
These observations have the hallmarks of a conservation law:
- A closed system is involved. Nothing is making an effort to twist the earth, the hydrogen atom, or the high-diver. They are isolated from rotation-changing influences, i.e., they are closed systems.
- Something remains unchanged. There appears to be a numerical quantity for measuring rotational motion such that the total amount of that quantity remains constant in a closed system.
- Something can be transferred back and forth without changing the total amount. In the photo of the old-fashioned high jump, a, the jumper wants to get his feet out in front of him so he can keep from doing a “face plant” when he lands. Bringing his feet forward would involve a certain quantity of counterclockwise rotation, but he didn't start out with any rotation when he left the ground. Suppose we consider counterclockwise as positive and clockwise as negative. The only way his legs can acquire some positive rotation is if some other part of his body picks up an equal amount of negative rotation. This is why he swings his arms up behind him, clockwise.
What numerical measure of rotational motion is conserved? Car engines and old-fashioned LP records have speeds of rotation measured in rotations per minute (r.p.m.), but the number of rotations per minute (or per second) is not a conserved quantity. A twirling figure skater, for instance, can pull her arms in to increase her r.p.m.'s. The first section of this chapter deals with the numerical definition of the quantity of rotation that results in a valid conservation law.
When most people think of rotation, they think of a solid object like a wheel rotating in a circle around a fixed point. Examples of this type of rotation, called rigid rotation or rigid-body rotation, include a spinning top, a seated child's swinging leg, and a helicopter's spinning propeller. Rotation, however, is a much more general phenomenon, and includes noncircular examples such as a comet in an elliptical orbit around the sun, or a cyclone, in which the core completes a circle more quickly than the outer parts.
If there is a numerical measure of rotational motion that is a conserved quantity, then it must include nonrigid cases like these, since nonrigid rotation can be traded back and forth with rigid rotation. For instance, there is a trick for finding out if an egg is raw or hardboiled. If you spin a hardboiled egg and then stop it briefly with your finger, it stops dead. But if you do the same with a raw egg, it springs back into rotation because the soft interior was still swirling around within the momentarily motionless shell. The pattern of flow of the liquid part is presumably very complex and nonuniform due to the asymmetric shape of the egg and the different consistencies of the yolk and the white, but there is apparently some way to describe the liquid's total amount of rotation with a single number, of which some percentage is given back to the shell when you release it.
The best strategy is to devise a way of defining the amount of rotation of a single small part of a system. The amount of rotation of a system such as a cyclone will then be defined as the total of all the contributions from its many small parts.
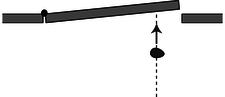
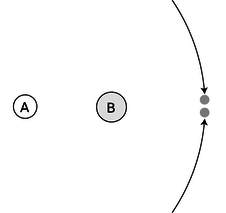
Figure b: An overhead view of a piece of putty being thrown at a door. Even though the putty is neither spinning nor traveling along a curve, we must define it has having some kind of “rotation” because it is able to make the door rotate.
The quest for a conserved quantity of rotation even requires us to broaden the rotation concept to include cases where the motion doesn't repeat or even curve around. If you throw a piece of putty at a door, (Figure b), the door will recoil and start rotating. The putty was traveling straight, not in a circle, but if there is to be a general conservation law that can cover this situation, it appears that we must describe the putty as having had some “rotation,” which it then gave up to the door. The best way of thinking about it is to attribute rotation to any moving object or part of an object that changes its angle in relation to the axis of rotation. In the putty-and-door example, the hinge of the door is the natural point to think of as an axis, and the putty changes its angle as seen by someone standing at the hinge, Figure c. For this reason, the conserved quantity we are investigating is called angular momentum. The symbol for angular momentum can't be “a” or “m,” since those are used for acceleration and mass, so the letter L is arbitrarily chosen instead.
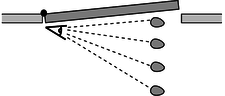
Figure c: As seen by someone standing at the axis, the putty changes its angular position. We therefore define it as having angular momentum.
Imagine a 1 kg blob of putty, thrown at the door at a speed of 1 m/s, which hits the door at a distance of 1 m from the hinge. We define this blob to have 1 unit of angular momentum. When it hits the door, the door will recoil and start rotating. We can use the speed at which the door recoils as a measure of the angular momentum the blob brought in.1
Experiments show, not surprisingly, that a 2 kg blob thrown in the same way makes the door rotate twice as fast, so the angular momentum of the putty blob must be proportional to mass,
\begin{equation*} L \propto m . \end{equation*}
Similarly, experiments show that doubling the velocity of the blob will have a doubling effect on the result, so its angular momentum must be proportional to its velocity as well,
\begin{equation*} L \propto mv . \end{equation*}
You have undoubtedly had the experience of approaching a closed door with one of those bar-shaped handles on it and pushing on the wrong side, the side close to the hinges. You feel like an idiot, because you have so little leverage that you can hardly budge the door. The same would be true with the putty blob.
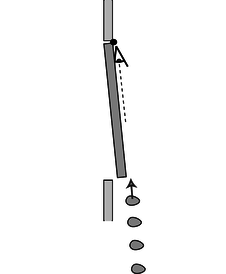
Figure d: A putty blob thrown directly at the axis has no angular motion, and therefore no angular momentum. It will not cause the door to rotate.
Experiments would show that the amount of rotation the blob can give to the door is proportional to the distance, r, from the axis of rotation, so angular momentum must be proportional to r as well,
\begin{equation*} L \propto mvr . \end{equation*}
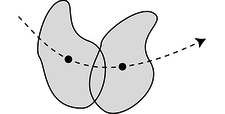
We are almost done, but there is one missing ingredient. We know on grounds of symmetry that a putty ball thrown directly inward toward the hinge will have no angular momentum to give to the door. After all, there would not even be any way to decide whether the ball's rotation was clockwise or counterclockwise in this situation. It is therefore only the component of the blob's velocity vector perpendicular to the door that should be counted in its angular momentum,
\begin{equation*} L = m v_{\perp} r . \end{equation*}
More generally, v_{\perp} should be thought of as the component of the object's velocity vector that is perpendicular to the line joining the object to the axis of rotation.
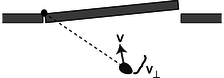
Figure e: Only the component of the velocity vector perpendicular to the line connecting the object to the axis should be counted into the definition of angular momentum.
We find that this equation agrees with the definition of the original putty blob as having one unit of angular momentum, and we can now see that the units of angular momentum are (\text{kg}\!\cdot\!\text{m}/\text{s})\!\cdot\!\text{m}, i.e., \text{kg}\!\cdot\!\text{m}^2/\text{s}. Summarizing, we have
\begin{equation*} L = m v_{\perp} r \text{[angular momentum of a particle in two dimensions]} , \end{equation*}
where m is the particle's mass, v_{\perp} is the component of its velocity vector perpendicular to the line joining it to the axis of rotation, and r is its distance from the axis. (Note that r is not necessarily the radius of a circle.) Positive and negative signs of angular momentum are used to describe opposite directions of rotation. The angular momentum of a finite-sized object or a system of many objects is found by dividing it up into many small parts, applying the equation to each part, and adding to find the total amount of angular momentum. (As implied by the word “particle,” matter isn't the only thing that can have angular momentum. Light can also have angular momentum, and the above equation would not apply to light.)
Conservation of angular momentum has been verified over and over again by experiment, and is now believed to be one of the most fundamental principles of physics, along with conservation of mass, energy, and momentum.
| Example 1: A figure skater pulls her arms in |
|---|
| When a figure skater is twirling, there is very little friction between her and the ice, so she is essentially a closed system, and her angular momentum is conserved. If she pulls her arms in, she is decreasing r for all the atoms in her arms.
Figure f: A figure skater pulls in her arms so that she can execute a spin more rapidly.
It would violate conservation of angular momentum if she then continued rotating at the same speed, i.e., taking the same amount of time for each revolution, because her arms' contributions to her angular momentum would have decreased, and no other part of her would have increased its angular momentum. This is impossible because it would violate conservation of angular momentum. If her total angular momentum is to remain constant, the decrease in r for her arms must be compensated for by an overall increase in her rate of rotation. That is, by pulling her arms in, she substantially reduces the time for each rotation. |
| Example 2: Earth's slowing rotation and the receding moon |
|---|
| The earth's rotation is actually slowing down very gradually, with the kinetic energy being dissipated as heat by friction between the land and the tidal bulges raised in the seas by the earth's gravity. Does this mean that angular momentum is not really perfectly conserved? No, it just means that the earth is not quite a closed system by itself. If we consider the earth and moon as a system, then the angular momentum lost by the earth must be gained by the moon somehow. In fact very precise measurements of the distance between the earth and the moon have been carried out by bouncing laser beams off of a mirror left there by astronauts, and these measurements show that the moon is receding from the earth at a rate of 4 centimeters per year! The moon's greater value of r means that it has a greater angular momentum, and the increase turns out to be exactly the amount lost by the earth. In the days of the dinosaurs, the days were significantly shorter, and the moon was closer and appeared bigger in the sky.
Figure g: A view of the earth-moon system from above the north pole. All distances have been highly distorted for legibility.
But what force is causing the moon to speed up, drawing it out into a larger orbit? It is the gravitational forces of the earth's tidal bulges. In figure g, the earth's rotation is counterclockwise (arrow). The moon's gravity creates a bulge on the side near it, because its gravitational pull is stronger there, and an “anti-bulge” on the far side, since its gravity there is weaker. For simplicity, let's focus on the tidal bulge closer to the moon. Its frictional force is trying to slow down the earth's rotation, so its force on the earth's solid crust is toward the bottom of the figure. By Newton's third law, the crust must thus make a force on the bulge which is toward the top of the figure. This causes the bulge to be pulled forward at a slight angle, and the bulge's gravity therefore pulls the moon forward, accelerating its orbital motion about the earth and flinging it outward. The result would obviously be extremely difficult to calculate directly, and this is one of those situations where a conservation law allows us to make precise quantitative statements about the outcome of a process when the calculation of the process itself would be prohibitively complex. |
Restriction to rotation in a plane
Is angular momentum a vector, or a scalar? It does have a direction in space, but it's a direction of rotation, not a straight-line direction like the directions of vectors such as velocity or force. It turns out that there is a way of defining angular momentum as a vector, but in this section the examples will be confined to a single plane of rotation, i.e., effectively two-dimensional situations. In this special case, we can choose to visualize the plane of rotation from one side or the other, and to define clockwise and counterclockwise rotation as having opposite signs of angular momentum. “Effectively” two-dimensional means that we can deal with objects that aren't flat, as long as the velocity vectors of all their parts lie in a plane.
Discussion Questions
◊ Conservation of plain old momentum, p, can be thought of as the greatly expanded and modified descendant of Galileo's original principle of inertia, that no force is required to keep an object in motion. The principle of inertia is counterintuitive, and there are many situations in which it appears superficially that a force is needed to maintain motion, as maintained by Aristotle. Think of a situation in which conservation of angular momentum, L, also seems to be violated, making it seem incorrectly that something external must act on a closed system to keep its angular momentum from “running down.”
4.1.2 Application to planetary motion
We now discuss the application of conservation of angular momentum to planetary motion, both because of its intrinsic importance and because it is a good way to develop a visual intuition for angular momentum.
Kepler's law of equal areas states that the area swept out by a planet in a certain length of time is always the same. Angular momentum had not been invented in Kepler's time, and he did not even know the most basic physical facts about the forces at work. He thought of this law as an entirely empirical and unexpectedly simple way of summarizing his data, a rule that succeeded in describing and predicting how the planets sped up and slowed down in their elliptical paths. It is now fairly simple, however, to show that the equal area law amounts to a statement that the planet's angular momentum stays constant.
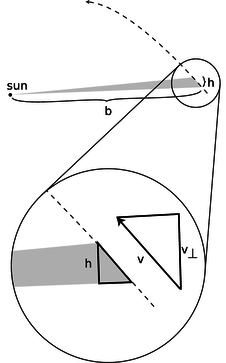
Figure h: The area swept out by a planet in its orbit.
There is no simple geometrical rule for the area of a pie wedge cut out of an ellipse, but if we consider a very short time interval, as shown in figure h, the shaded shape swept out by the planet is very nearly a triangle. We do know how to compute the area of a triangle. It is one half the product of the base and the height:
We wish to relate this to angular momentum, which contains the variables r and v_{\perp}. If we consider the sun to be the axis of rotation, then the variable r is identical to the base of the triangle, r=b. Referring to the magnified portion of the figure, v_{\perp} can be related to h, because the two right triangles are similar:
The area can thus be rewritten as
The distance traveled equals |\mathbf{v}|\Delta t, so this simplifies to
We have found the following relationship between angular momentum and the rate at which area is swept out:
The factor of 2 in front is simply a matter of convention, since any conserved quantity would be an equally valid conserved quantity if you multiplied it by a constant. The factor of m was not relevant to Kepler, who did not know the planets' masses, and who was only describing the motion of one planet at a time.
We thus find that Kepler's equal-area law is equivalent to a statement that the planet's angular momentum remains constant. But wait, why should it remain constant? --- the planet is not a closed system, since it is being acted on by the sun's gravitational force. There are two valid answers. The first is that it is actually the total angular momentum of the sun plus the planet that is conserved. The sun, however, is millions of times more massive than the typical planet, so it accelerates very little in response to the planet's gravitational force. It is thus a good approximation to say that the sun doesn't move at all, so that no angular momentum is transferred between it and the planet.
The second answer is that to change the planet's angular momentum requires not just a force but a force applied in a certain way. Later in this section (starting on page 254) we discuss the transfer of angular momentum by a force, but the basic idea here is that a force directly in toward the axis does not change the angular momentum.
Discussion Questions
◊ Suppose an object is simply traveling in a straight line at constant speed. If we pick some point not on the line and call it the axis of rotation, is area swept out by the object at a constant rate?
◊

i / Discussion question B.
The figure is a strobe photo of a pendulum bob, taken from underneath the pendulum looking straight up. The black string can't be seen in the photograph. The bob was given a slight sideways push when it was released, so it did not swing in a plane. The bright spot marks the center, i.e., the position the bob would have if it hung straight down at us. Does the bob's angular momentum appear to remain constant if we consider the center to be the axis of rotation?
4.1.3 Two theorems about angular momentum
With plain old momentum, \mathbf{p}, we had the freedom to work in any inertial frame of reference we liked. The same object could have different values of momentum in two different frames, if the frames were not at rest with respect to each other. Conservation of momentum, however, would be true in either frame. As long as we employed a single frame consistently throughout a calculation, everything would work.
The same is true for angular momentum, and in addition there is an ambiguity that arises from the definition of an axis of rotation. For a wheel, the natural choice of an axis of rotation is obviously the axle, but what about an egg rotating on its side? The egg has an asymmetric shape, and thus no clearly defined geometric center. A similar issue arises for a cyclone, which does not even have a sharply defined shape, or for a complicated machine with many gears. The following theorem, the first of two presented in this section, explains how to deal with this issue. Although I have put descriptive titles above both theorems, they have no generally accepted names. The proofs, given on page 913, use the vector cross-product technique introduced in section 4.3, which greatly simplifies them.
The choice of axis theorem. It is entirely arbitrary what point one defines as the axis for purposes of calculating angular momentum. If a closed system's angular momentum is conserved when calculated with one choice of axis, then it will be conserved for any other choice of axis. Likewise, any inertial frame of reference may be used. The theorem also holds in the case where the system is not closed, but the total external force is zero.
| Example 3: Colliding asteroids described with different axes |
|---|
| Observers on planets A and B both see the two asteroids colliding. The asteroids are of equal mass and their impact speeds are the same. Astronomers on each planet decide to define their own planet as the axis of rotation. Planet A is twice as far from the collision as planet B. The asteroids collide and stick. For simplicity, assume planets A and B are both at rest.
Figure j: Two asteroids collide.
With planet A as the axis, the two asteroids have the same amount of angular momentum, but one has positive angular momentum and the other has negative. Before the collision, the total angular momentum is therefore zero. After the collision, the two asteroids will have stopped moving, and again the total angular momentum is zero. The total angular momentum both before and after the collision is zero, so angular momentum is conserved if you choose planet A as the axis. The only difference with planet B as axis is that r is smaller by a factor of two, so all the angular momenta are halved. Even though the angular momenta are different than the ones calculated by planet A, angular momentum is still conserved. The earth spins on its own axis once a day, but simultaneously travels in its circular one-year orbit around the sun, so any given part of it traces out a complicated loopy path. It would seem difficult to calculate the earth's angular momentum, but it turns out that there is an intuitively appealing shortcut: we can simply add up the angular momentum due to its spin plus that arising from its center of mass's circular motion around the sun. This is a special case of the following general theorem: The spin theorem. An object's angular momentum with respect to some outside axis A can be found by adding up two parts:
|
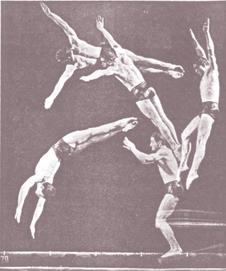
k / Everyone has a strong tendency to think of the diver as rotating about his own center of mass. However, he is flying in an arc, and he also has angular momentum because of this motion.
| Example 4: A system with its center of mass at rest |
|---|
| In the special case of an object whose center of mass is at rest, the spin theorem implies that the object's angular momentum is the same regardless of what axis we choose. (This is an even stronger statement than the choice of axis theorem, which only guarantees that angular momentum is conserved for any given choice of axis, without specifying that it is the same for all such choices.) |
| Example 5: Angular momentum of a rigid object |
|---|
| \triangleright A motorcycle wheel has almost all its mass concentrated at the outside. If the wheel has mass m and radius r, and the time required for one revolution is T, what is the spin part of its angular momentum?
l / This rigid object has angular momentum both because it is spinning about its center of mass and because it is moving through space.
\triangleright This is an example of the commonly encountered special case of rigid motion, as opposed to the rotation of a system like a hurricane in which the different parts take different amounts of time to go around. We don't really have to go through a laborious process of adding up contributions from all the many parts of a wheel, because they are all at about the same distance from the axis, and are all moving around the axis at about the same speed. The velocity is all perpendicular to the spokes, \begin{align*} v_{\perp} &= (\text{circumference})/ T \\ &= 2\pi r/ T \end{align*} and the angular momentum of the wheel about its center is \begin{align*} L &= mv_{\perp} r \\ &= m(2\pi r/ T) r \\ &= 2\pi mr^2/ T . \end{align*} |
Note that although the factors of 2\pi in this expression is peculiar to a wheel with its mass concentrated on the rim, the proportionality to m/T would have been the same for any other rigidly rotating object. Although an object with a noncircular shape does not have a radius, it is also true in general that angular momentum is proportional to the square of the object's size for fixed values of m and T. For instance doubling an object's size doubles both the v_{\perp} and r factors in the contribution of each of its parts to the total angular momentum, resulting in an overall factor of four increase.
4.1.4 Torque
Force is the rate of transfer of momentum. The corresponding quantity in the case of angular momentum is called torque (rhymes with “fork”). Where force tells us how hard we are pushing or pulling on something, torque indicates how hard we are twisting on it. Torque is represented by the Greek letter tau, \tau, and the rate of change of an object's angular momentum equals the total torque acting on it,
\begin{equation*} \tau_{total} = dL/dt . \end{equation*}
Torque distinguished from force
Of course a force is necessary in order to create a torque --- you can't twist a screw without pushing on the wrench --- but force and torque are two different things. One distinction between them is direction. We use positive and negative signs to represent forces in the two possible directions along a line. The direction of a torque, however, is clockwise or counterclockwise, not a linear direction.
The other difference between torque and force is a matter of leverage. A given force applied at a door's knob will change the door's angular momentum twice as rapidly as the same force applied halfway between the knob and the hinge. The same amount of force produces different amounts of torque in these two cases.
It's possible to have a zero total torque with a nonzero total force. An airplane with four jet engines would be designed so that their forces are balanced on the left and right. Their forces are all in the same direction, but the clockwise torques of two of the engines are canceled by the counterclockwise torques of the other two, giving zero total torque.
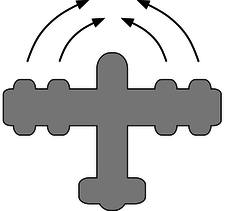
Figure m: The plane's four engines produce zero total torque but not zero total force.
Conversely we can have zero total force and nonzero total torque. A merry-go-round's engine needs to supply a nonzero torque on it to bring it up to speed, but there is zero total force on it. If there was not zero total force on it, its center of mass would accelerate!
Relationship between force and torque
How do we calculate the amount of torque produced by a given force? Since it depends on leverage, we should expect it to depend on the distance between the axis and the point of application of the force. I'll work out an equation relating torque to force for a particular very simple situation, and give a more rigorous derivation on page 284, after developing some mathematical techniques that dramatically shorten and simplify the proof.
Consider a pointlike object which is initially at rest at a distance r from the axis we have chosen for defining angular momentum. We first observe that a force directly inward or outward, along the line connecting the axis to the object, does not impart any angular momentum to the object.
A force perpendicular to the line connecting the axis and the object does, however, make the object pick up angular momentum. Newton's second law gives
and using a=dv/dt we find the velocity the object acquires after a time dt,
We're trying to relate force to a change in angular momentum, so we multiply both sides of the equation by mr to give
Dividing by dt gives the torque:
If a force acts at an angle other than 0 or 90° with respect to the line joining the object and the axis, it would be only the component of the force perpendicular to the line that would produce a torque,
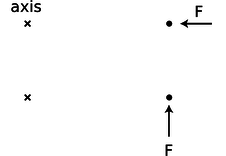
n / The simple physical situation we use to derive an equation for torque. A force that points directly in at or out away from the axis produces neither clockwise nor counterclockwise angular momentum. A force in the perpendicular direction does transfer angular momentum.
Although this result was proved under a simplified set of circumstances, it is more generally valid:2
\mythmhdr{Relationship between force and torque} The rate at which a force transfers angular momentum to an object, i.e., the torque produced by the force, is given by
where r is the distance from the axis to the point of application of the force, and F_{\perp} is the component of the force that is perpendicular to the line joining the axis to the point of application.
The equation is stated with absolute value signs because the positive and negative signs of force and torque indicate different things, so there is no useful relationship between them. The sign of the torque must be found by physical inspection of the case at hand.
From the equation, we see that the units of torque can be written as newtons multiplied by meters. Metric torque wrenches are calibrated in \text{N}\!\cdot\!\text{m}, but American ones use foot-pounds, which is also a unit of distance multiplied by a unit of force. We know from our study of mechanical work that newtons multiplied by meters equal joules, but torque is a completely different quantity from work, and nobody writes torques with units of joules, even though it would be technically correct.
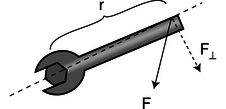
o / The geometric relationships referred to in the relationship between force and torque.
p / Self-check.
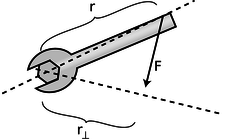
q / Visualizing torque in terms of r_\perp.
Exercise \PageIndex{1}
Compare the magnitudes and signs of the four torques shown in figure p. (answer in the back of the PDF version of the book)
| Example 6: How torque depends on the direction of the force |
|---|
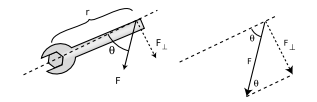
| \triangleright How can the torque applied to the wrench in the figure be expressed in terms of r, | F|, and the angle \theta? \triangleright The force vector and its F_{\perp} component form the hypotenuse and one leg of a right triangle,
and the interior angle opposite to F_{\perp} equals \theta. The absolute value of F_{\perp} can thus be expressed as \begin{equation*} F_{\perp} = |\mathbf{F}|\ \text{sin}\:\theta , \end{equation*} leading to \begin{equation*} |\tau| = r |\mathbf{F}|\ \text{sin}\:\theta . \end{equation*} Sometimes torque can be more neatly visualized in terms of the quantity r_{\perp} shown in the figure on the left, which gives us a third way of expressing the relationship between torque and force: \begin{equation*} |\tau| = r_{\perp} |F| . \end{equation*} Of course you wouldn't want to go and memorize all three equations for torque. Starting from any one of them you could easily derive the other two using trigonometry. Familiarizing yourself with them can however clue you in to easier avenues of attack on certain problems. |
The torque due to gravity
Up until now we've been thinking in terms of a force that acts at a single point on an object, such as the force of your hand on the wrench. This is of course an approximation, and for an extremely realistic calculation of your hand's torque on the wrench you might need to add up the torques exerted by each square millimeter where your skin touches the wrench. This is seldom necessary. But in the case of a gravitational force, there is never any single point at which the force is applied. Our planet is exerting a separate tug on every brick in the Leaning Tower of Pisa, and the total gravitational torque on the tower is the sum of the torques contributed by all the little forces. Luckily there is a trick that allows us to avoid such a massive calculation. It turns out that for purposes of computing the total gravitational torque on an object, you can get the right answer by just pretending that the whole gravitational force acts at the object's center of mass.
| Example 7: Gravitational torque on an outstretched arm |
|---|
| \triangleright Your arm has a mass of 3.0 kg, and its center of mass is 30 cm from your shoulder. What is the gravitational torque on your arm when it is stretched out horizontally to one side, taking the shoulder to be the axis?
r / Example 7.
\triangleright The total gravitational force acting on your arm is \begin{equation*} |\mathbf{F}| = ( 3.0\ \text{kg})( 9.8\ \text{m}/\text{s}^2) = 29\ \text{N} . \end{equation*} For the purpose of calculating the gravitational torque, we can treat the force as if it acted at the arm's center of mass. The force is straight down, which is perpendicular to the line connecting the shoulder to the center of mass, so \begin{equation*} F_{\perp} = |\mathbf{F}| = 29\ \text{N} . \end{equation*} Continuing to pretend that the force acts at the center of the arm, r equals 30 cm = 0.30 m, so the torque is \begin{equation*} \tau = r\: F_{\perp} = 9\ \text{N}\cdot\text{m} . \end{equation*} |
Discussion Questions
◊ This series of discussion questions deals with past students' incorrect reasoning about the following problem.
Suppose a comet is at the point in its orbit shown in the figure. The only force on the comet is the sun's gravitational force. Throughout the question, define all torques and angular momenta using the sun as the axis.
(1) Is the sun producing a nonzero torque on the comet? Explain.
(2) Is the comet's angular momentum increasing, decreasing, or staying the same? Explain.
Explain what is wrong with the following answers. In some cases, the answer is correct, but the reasoning leading up to it is wrong.
(a) Incorrect answer to part (1): “Yes, because the sun is exerting a force on the comet, and the comet is a certain distance from the sun.”
(b) Incorrect answer to part (1): “No, because the torques cancel out.”
(c) Incorrect answer to part (2): “Increasing, because the comet is speeding up.”

u / Discussion question A.
◊ You whirl a rock over your head on the end of a string, and gradually pull in the string, eventually cutting the radius in half. What happens to the rock's angular momentum? What changes occur in its speed, the time required for one revolution, and its acceleration? Why might the string break?
◊ A helicopter has, in addition to the huge fan blades on top, a smaller propeller mounted on the tail that rotates in a vertical plane. Why?
◊
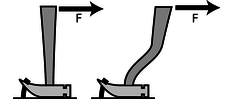
s / Discussion question D.
Which claw hammer would make it easier to get the nail out of the wood if the same force was applied in the same direction?
◊

t / Discussion question E.
The photo shows an amusement park ride whose two cars rotate in opposite directions. Why is this a good design?
4.1.5 Applications to statics

v / The windmills are not closed systems, but angular momentum is being transferred out of them at the same rate it is transferred in, resulting in constant angular momentum. To get an idea of the huge scale of the modern windmill farm, note the sizes of the trucks and trailers.
In chapter 2 I defined equilibrium as a situation where the interaction energy is minimized. This is the same as a condition of zero total force, or constant momentum. Thus a car is in equilibrium not just when it is parked but also when it is cruising down a straight road with constant momentum.
Likewise there are many cases where a system is not closed but maintains constant angular momentum. When a merry-go-round is running at constant angular momentum, the engine's torque is being canceled by the torque due to friction.
It's not enough for a boat not to sink --- we'd also like to avoid having it capsize. For this reason, we now redefine equilibrium as follows.
When an object has constant momentum and constant angular momentum, we say that it is in equilibrium. Again, this is a scientific redefinition of the common English word, since in ordinary speech nobody would describe a car spinning out on an icy road as being in equilibrium.
Very commonly, however, we are interested in cases where an object is not only in equilibrium but also at rest, and this corresponds more closely to the usual meaning of the word. Statics is the branch of physics concerned with problems such as these.
Solving statics problems is now simply a matter of applying and combining some things you already know:
- You know the behaviors of the various types of forces, for example that a frictional force is always parallel to the surface of contact.
- You know about vector addition of forces. It is the vector sum of the forces that must equal zero to produce equilibrium.
- You know about torque. The total torque acting on an object must be zero if it is to be in equilibrium.
- You know that the choice of axis is arbitrary, so you can make a choice of axis that makes the problem easy to solve.
In general, this type of problem could involve four equations in four unknowns: three equations that say the force components add up to zero, and one equation that says the total torque is zero. Most cases you'll encounter will not be this complicated. In the example below, only the equation for zero total torque is required in order to get an answer.
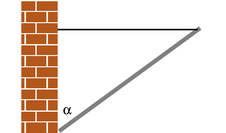
| Example 8: A flagpole |
|---|
| \triangleright A 10-kg flagpole is being held up by a lightweight horizontal cable, and is propped against the foot of a wall as shown in the figure. If the cable is only capable of supporting a tension of 70 N, how great can the angle \alpha be without breaking the cable?
w / Example 8.
\triangleright All three objects in the figure are supposed to be in equilibrium: the pole, the cable, and the wall. Whichever of the three objects we pick to investigate, all the forces and torques on it have to cancel out. It is not particularly helpful to analyze the forces and torques on the wall, since it has forces on it from the ground that are not given and that we don't want to find. We could study the forces and torques on the cable, but that doesn't let us use the given information about the pole. The object we need to analyze is the pole. The pole has three forces on it, each of which may also result in a torque: (1) the gravitational force, (2) the cable's force, and (3) the wall's force. We are free to define an axis of rotation at any point we wish, and it is helpful to define it to lie at the bottom end of the pole, since by that definition the wall's force on the pole is applied at r=0 and thus makes no torque on the pole. This is good, because we don't know what the wall's force on the pole is, and we are not trying to find it. With this choice of axis, there are two nonzero torques on the pole, a counterclockwise torque from the cable and a clockwise torque from gravity. Choosing to represent counterclockwise torques as positive numbers, and using the equation |\boldsymbol{\tau}| =r|F| \sin \theta, we have \begin{equation*} r_{cable} |F_{cable}| \sin \theta_{cable} - r_{grav}|F_{grav}|\sin \theta_{grav} = 0 . \end{equation*} A little geometry gives \theta_{cable}=90°-\alpha and \theta_{grav}=\alpha, so \begin{equation*} r_{cable} |F_{cable}| \sin (90°-\alpha) - r_{grav}|F_{grav}| \sin \alpha = 0 . \end{equation*} The gravitational force can be considered as acting at the pole's center of mass, i.e., at its geometrical center, so r_{cable} is twice r_{grav}, and we can simplify the equation to read \begin{equation*} 2 |F_{cable}| \sin (90°-\alpha) - |F_{grav}| \sin \alpha = 0 . \end{equation*} These are all quantities we were given, except for \alpha, which is the angle we want to find. To solve for \alpha we need to use the trig identity \sin (90°-x)= \cos x, \begin{equation*} 2 |F_{cable}| \cos \alpha - |F_{grav}| \sin \alpha = 0 , \end{equation*} which allows us to find \begin{align*} \tan\alpha &= 2\frac{|\mathbf{F}_{cable}|}{|\mathbf{F}_{grav}|}\\ \alpha &= \tan^{-1}\left(2\frac{|\mathbf{F}_{cable}|}{|\mathbf{F}_{grav}|}\right)\\ &= \tan^{-1}\left(2\times\frac{70\ \text{N}}{98\ \text{N}}\right)\\ &= 55° . \end{align*} |
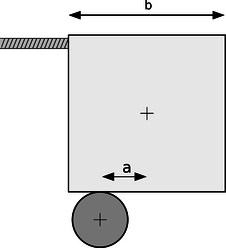
| Example 9: Art! |
|---|
| \triangleright The abstract sculpture shown in figure x contains a cube of mass m and sides of length b. The cube rests on top of a cylinder, which is off-center by a distance a. Find the tension in the cable.
x / Example 9.
\triangleright There are four forces on the cube: a gravitational force mg, the force F_T from the cable, the upward normal force from the cylinder, F_N, and the horizontal static frictional force from the cylinder, F_s. The total force on the cube in the vertical direction is zero: \begin{equation*} F_N-mg = 0 . \end{equation*} |
As our axis for defining torques, it's convenient to choose the point of contact between the cube and the cylinder, because then neither F_s nor F_N makes any torque. The cable's torque is counterclockwise, and the torque due to gravity is clockwise. and the cylinder's torque is clockwise. Letting counterclockwise torques be positive, and using the convenient equation \tau=r_\perp F, we find the equation for the total torque:
We could also write down the equation saying that the total horizontal force is zero, but that would bring in the cylinder's frictional force on the cube, which we don't know and don't need to find. We already have two equations in the two unknowns F_T and F_N, so there's no need to make it into three equations in three unknowns. Solving the first equation for F_N=mg, we then substitute into the second equation to eliminate F_N, and solve for F_T=(a/b)mg.
Why is one equilibrium stable and another unstable? Try pushing your own nose to the left or the right. If you push it a millimeter to the left, it responds with a gentle force to the right. If you push it a centimeter to the left, its force on your finger becomes much stronger. The defining characteristic of a stable equilibrium is that the farther the object is moved away from equilibrium, the stronger the force is that tries to bring it back.
The opposite is true for an unstable equilibrium. In the top figure, the ball resting on the round hill theoretically has zero total force on it when it is exactly at the top. But in reality the total force will not be exactly zero, and the ball will begin to move off to one side. Once it has moved, the net force on the ball is greater than it was, and it accelerates more rapidly. In an unstable equilibrium, the farther the object gets from equilibrium, the stronger the force that pushes it farther from equilibrium.
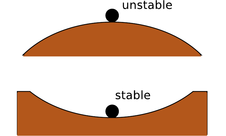
y / Stable and unstable equilibria.
This idea can be rephrased in terms of energy. The difference between the stable and unstable equilibria shown in figure y is that in the stable equilibrium, the energy is at a minimum, and moving to either side of equilibrium will increase it, whereas the unstable equilibrium represents a maximum.
Note that we are using the term “stable” in a weaker sense than in ordinary speech. A domino standing upright is stable in the sense we are using, since it will not spontaneously fall over in response to a sneeze from across the room or the vibration from a passing truck. We would only call it unstable in the technical sense if it could be toppled by any force, no matter how small. In everyday usage, of course, it would be considered unstable, since the force required to topple it is so small.

z / The dancer's equilibrium is unstable. If she didn't constantly make tiny adjustments, she would tip over.
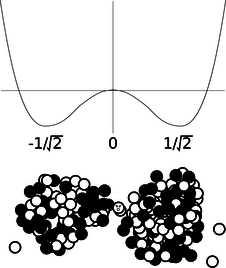
| Example 10: Application of Calculus |
|---|
| \triangleright Nancy Neutron is living in a uranium nucleus that is undergoing fission. Nancy's nuclear energy as a function of position can be approximated by U=x^4-x^2, where all the units and numerical constants have been suppressed for simplicity. Use calculus to locate the equilibrium points, and determine whether they are stable or unstable.
aa / Example 10.
\triangleright The equilibrium points occur where the U is at a minimum or maximum, and minima and maxima occur where the derivative (which equals minus the force on Nancy) is zero. This derivative is dU/dx=4x^3-2x, and setting it equal to zero, we have x=0, \pm1/\sqrt{2}. Minima occur where the second derivative is positive, and maxima where it is negative. The second derivative is 12x^2-2, which is negative at x=0 (unstable) and positive at x=\pm1/\sqrt{2} (stable). Interpretation: the graph of U is shaped like a rounded letter `W,' with the two troughs representing the two halves of the splitting nucleus. Nancy is going to have to decide which half she wants to go with. |
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.