8.E: Relativity (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
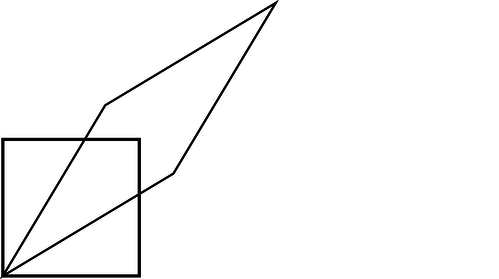
1. The figure illustrates a Lorentz transformation using the conventions employed in section 7.2. For simplicity, the transformation chosen is one that lengthens one diagonal by a factor of 2. Since Lorentz transformations preserve area, the other diagonal is shortened by a factor of 2. Let the original frame of reference, depicted with the square, be A, and the new one B. (a) By measuring with a ruler on the figure, show that the velocity of frame B relative to frame A is 0.6c. (b) Print out a copy of the page. With a ruler, draw a third parallelogram that represents a second successive Lorentz transformation, one that lengthens the long diagonal by another factor of 2. Call this third frame C. Use measurements with a ruler to determine frame C's velocity relative to frame A. Does it equal double the velocity found in part a? Explain why it should be expected to turn out the way it does.(answer check available at lightandmatter.com)
2. Astronauts in three different spaceships are communicating with each other. Those aboard ships A and B agree on the rate at which time is passing, but they disagree with the ones on ship C.
(a) Alice is aboard ship A. How does she describe the motion of her own ship, in its frame of reference?
(b) Describe the motion of the other two ships according to Alice.
(c) Give the description according to Betty, whose frame of reference is ship B.
(d) Do the same for Cathy, aboard ship C.
3. What happens in the equation for γ when you put in a negative number for v? Explain what this means physically, and why it makes sense.
4. The Voyager 1 space probe, launched in 1977, is moving faster relative to the earth than any other human-made object, at 17,000 meters per second.
(a) Calculate the probe's γ.
(b) Over the course of one year on earth, slightly less than one year passes on the probe. How much less? (There are 31 million seconds in a year.)(answer check available at lightandmatter.com)
5. In example 2 on page 391, I remarked that accelerating a macroscopic (i.e., not microscopic) object to close to the speed of light would require an unreasonable amount of energy. Suppose that the starship Enterprise from Star Trek has a mass of 8.0×107 kg, about the same as the Queen Elizabeth 2. Compute the kinetic energy it would have to have if it was moving at half the speed of light. Compare with the total energy content of the world's nuclear arsenals, which is about 1021 J.(answer check available at lightandmatter.com)
6. The earth is orbiting the sun, and therefore is contracted relativistically in the direction of its motion. Compute the amount by which its diameter shrinks in this direction.(answer check available at lightandmatter.com)
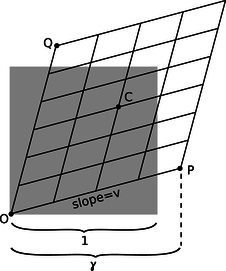
a / Problem 7.
7. In this homework problem, you'll fill in the steps of the algebra required in order to find the equation for γ on page 389. To keep the algebra simple, let the time t in figure k equal 1, as suggested in the figure accompanying this homework problem. The original square then has an area of 1, and the transformed parallelogram must also have an area of 1. (a) Prove that point P is at x=vγ, so that its (t,x) coordinates are (γ,vγ). (b) Find the (t,x) coordinates of point Q. (c) Find the length of the short diagonal connecting P and Q. (d) Average the coordinates of P and Q to find the coordinates of the midpoint C of the parallelogram, and then find distance OC. (e) Find the area of the parallelogram by computing twice the area of triangle PQO. [Hint: You can take PQ to be the base of the triangle.] (f) Set this area equal to 1 and solve for γ to prove γ=1/√1−v2.(answer check available at lightandmatter.com)
8. (a) A free neutron (as opposed to a neutron bound into an atomic nucleus) is unstable, and undergoes beta decay (which you may want to review). The masses of the particles involved are as follows:
| neutron | 1.67495×10 − 27 kg |
| proton | 1.67265×10 − 27 kg |
| electron | 0.00091×10 − 27 kg |
| antineutrino | < 10 − 35 kg |
Find the energy released in the decay of a free neutron. (answer check available at lightandmatter.com)
(b) Neutrons and protons make up essentially all of the mass of the ordinary matter around us. We observe that the universe around us has no free neutrons, but lots of free protons (the nuclei of hydrogen, which is the element that 90% of the universe is made of). We find neutrons only inside nuclei along with other neutrons and protons, not on their own.
If there are processes that can convert neutrons into protons, we might imagine that there could also be proton-to-neutron conversions, and indeed such a process does occur sometimes in nuclei that contain both neutrons and protons: a proton can decay into a neutron, a positron, and a neutrino. A positron is a particle with the same properties as an electron, except that its electrical charge is positive (see chapter 7). A neutrino, like an antineutrino, has negligible mass.
Although such a process can occur within a nucleus, explain why it cannot happen to a free proton. (If it could, hydrogen would be radioactive, and you wouldn't exist!)
9. (a) Find a relativistic equation for the velocity of an object in terms of its mass and momentum (eliminating γ).(answer check available at lightandmatter.com)
(b) Show that your result is approximately the same as the classical value, p/m, at low velocities.
(c) Show that very large momenta result in speeds close to the speed of light.
10. (a) Show that for v=(3/5)c, γ comes out to be a simple fraction.
(b) Find another value of v for which γ is a simple fraction.
11. An object moving at a speed very close to the speed of light is referred to as ultrarelativistic. Ordinarily (luckily) the only ultrarelativistic objects in our universe are subatomic particles, such as cosmic rays or particles that have been accelerated in a particle accelerator.
(a) What kind of number is γ for an ultrarelativistic particle?
(b) Repeat example 18 on page 418, but instead of very low, nonrelativistic speeds, consider ultrarelativistic speeds.
(c) Find an equation for the ratio E/p. The speed may be relativistic, but don't assume that it's ultrarelativistic.(answer check available at lightandmatter.com)
(d) Simplify your answer to part c for the case where the speed is ultrarelativistic.(answer check available at lightandmatter.com)
(e) We can think of a beam of light as an ultrarelativistic object --- it certainly moves at a speed that's sufficiently close to the speed of light! Suppose you turn on a one-watt flashlight, leave it on for one second, and then turn it off. Compute the momentum of the recoiling flashlight, in units of kg⋅m/s.(answer check available at lightandmatter.com)
(f) Discuss how your answer in part e relates to the correspondence principle.
12. As discussed in chapter 6, the speed at which a disturbance travels along a string under tension is given by v=√T/μ, where μ is the mass per unit length, and T is the tension.
(a) Suppose a string has a density ρ, and a cross-sectional area A. Find an expression for the maximum tension that could possibly exist in the string without producing v>c, which is impossible according to relativity. Express your answer in terms of ρ, A, and c. The interpretation is that relativity puts a limit on how strong any material can be.(answer check available at lightandmatter.com)
(b) Every substance has a tensile strength, defined as the force per unit area required to break it by pulling it apart. The tensile strength is measured in units of N/m2, which is the same as the pascal (Pa), the mks unit of pressure. Make a numerical estimate of the maximum tensile strength allowed by relativity in the case where the rope is made out of ordinary matter, with a density on the same order of magnitude as that of water. (For comparison, kevlar has a tensile strength of about 4×109 Pa, and there is speculation that fibers made from carbon nanotubes could have values as high as 6×1010 Pa.)(answer check available at lightandmatter.com)
(c) A black hole is a star that has collapsed and become very dense, so that its gravity is too strong for anything ever to escape from it. For instance, the escape velocity from a black hole is greater than c, so a projectile can't be shot out of it. Many people, when they hear this description of a black hole in terms of an escape velocity greater than c, wonder why it still wouldn't be possible to extract an object from a black hole by other means than launching it out as a projectile. For example, suppose we lower an astronaut into a black hole on a rope, and then pull him back out again. Why might this not work?
13. (a) A charged particle is surrounded by a uniform electric field. Starting from rest, it is accelerated by the field to speed v after traveling a distance d. Now it is allowed to continue for a further distance 3d, for a total displacement from the start of 4d. What speed will it reach, assuming classical physics?
(b) Find the relativistic result for the case of v=c/2.
14. Problem 14 has been deleted.
15. Expand the equation K=m(γ−1) in a Taylor series, and find the first two nonvanishing terms. Show that the first term is the nonrelativistic expression for kinetic energy.
16. Expand the relativistic equation for momentum in a Taylor series, and find the first two nonvanishing terms. Show that the first term is the classical expression.
17. (solution in the pdf version of the book) As promised in subsection 7.2.8, this problem will lead you through the steps of finding an equation for the combination of velocities in relativity, generalizing the numerical result found in problem 1. Suppose that A moves relative to B at velocity u, and B relative to C at v. We want to find A's velocity w relative to C, in terms of u and v. Suppose that A emits light with a certain frequency. This will be observed by B with a Doppler shift D(u). C detects a further shift of D(v) relative to B. We therefore expect the Doppler shifts to multiply, D(w)=D(u)D(v), and this provides an implicit rule for determining w if u and v are known. (a) Using the expression for D given in section 7.2.8, write down an equation relating u, v, and w. (b) Solve for w in terms of u and v. (c) Show that your answer to part b satisfies the correspondence principle.
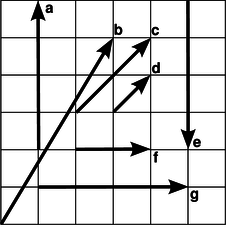
b / Problem 18.
18. The figure shows seven four-vectors, represented in a two-dimensional plot of x versus t. All the vectors have y and z components that are zero. Which of these vectors are congruent to others, i.e., which represent spacetime intervals that are equal to one another?
19. Four-vectors can be timelike, lightlike, or spacelike. What can you say about the inherent properties of particles whose momentum four-vectors fall in these various categories?
20. The following are the three most common ways in which gamma rays interact with matter:
Photoelectric effect: The gamma ray hits an electron, is annihilated, and gives all of its energy to the electron.
Compton scattering: The gamma ray bounces off of an electron, exiting in some direction with some amount of energy.
Pair production: The gamma ray is annihilated, creating an electron and a positron.
Example a href="#eg:no-pair-prod-in-vacuum">23 on p. 420 shows that pair production can't occur in a vacuum due to conservation of the energy-momentum four-vector. What about the other two processes? Can the photoelectric effect occur without the presence of some third particle such as an atomic nucleus? Can Compton scattering happen without a third particle?
21. Expand the relativistic equation for the longitudinal Doppler shift of light D(v) in a Taylor series, and find the first two nonvanishing terms. Show that these two terms agree with the nonrelativistic expression, so that any relativistic effect is of higher order in v.
22. Prove, as claimed in the caption of figure a on p. 424, that S-180°=4(s-180°), where S is the sum of the angles of the large equilateral triangle and s is the corresponding sum for one of the four small ones.(solution in the pdf version of the book)
23. If a two-dimensional being lived on the surface of a cone, would it say that its space was curved, or not?
24. (a) Verify that the equation 1-gh/c^2 for the gravitational Doppler shift and gravitational time dilation has units that make sense. (b) Does this equation satisfy the correspondence principle?
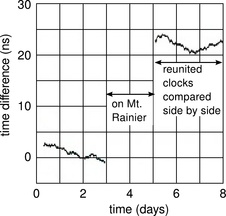
c / Problem 25b. Redrawn from Van Baak, Physics Today 60 (2007) 16.
25. (a) Calculate the Doppler shift to be expected in the Pound-Rebka experiment described on p. 429. (b) In the 1978 Iijima mountain-valley experiment (p. 384), analysis was complicated by the clock's sensitivity to pressure, humidity, and temperature. A cleaner version of the experiment was done in 2005 by hobbyist Tom Van Baak. He put his kids and three of his atomic clocks in a minivan and drove from Bellevue, Washington to a lodge on Mount Rainier, 1340 meters higher in elevation. At home, he compared the clocks to others that had stayed at his house. Verify that the effect shown in the graph is as predicted by general relativity.
26. The International Space Station orbits at an altitude of about 350 km and a speed of about 8000 m/s relative to the ground. Compare the gravitational and kinematic time dilations. Over all, does time run faster on the ISS than on the ground, or more slowly?
27. Section 7.4.3 presented a Newtonian estimate of how compact an object would have to be in order to be a black hole. Although this estimate is not really right, it turns out to give the right answer to within about a factor of 2. To roughly what size would the earth have to be compressed in order to become a black hole?
28. Clock A sits on a desk. Clock B is tossed up in the air from the same height as the desk and then comes back down. Compare the elapsed times. \hwhint{hwhint:tossed-clock} (solution in the pdf version of the book)
29. The angular defect d of a triangle (measured in radians) is defined as s-\pi, where s is the sum of the interior angles. The angular defect is proportional to the area A of the triangle. Consider the geometry measured by a two-dimensional being who lives on the surface of a sphere of radius R. First find some triangle on the sphere whose area and angular defect are easy to calculate. Then determine the general equation for d in terms of A and R.(answer check available at lightandmatter.com)
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


