9.1: The Electric Glue
- Page ID
- 962
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Where the telescope ends, the microscope begins. Which of the two has the grander view? -- Victor Hugo
His father died during his mother's pregnancy. Rejected by her as a boy, he was packed off to boarding school when she remarried. He himself never married, but in middle age he formed an intense relationship with a much younger man, a relationship that he terminated when he underwent a psychotic break. Following his early scientific successes, he spent the rest of his professional life mostly in frustration over his inability to unlock the secrets of alchemy.
The man being described is Isaac Newton, but not the triumphant Newton of the standard textbook hagiography. Why dwell on the sad side of his life? To the modern science educator, Newton's lifelong obsession with alchemy may seem an embarrassment, a distraction from his main achievement, the creation the modern science of mechanics. To Newton, however, his alchemical researches were naturally related to his investigations of force and motion. What was radical about Newton's analysis of motion was its universality: it succeeded in describing both the heavens and the earth with the same equations, whereas previously it had been assumed that the sun, moon, stars, and planets were fundamentally different from earthly objects. But Newton realized that if science was to describe all of nature in a unified way, it was not enough to unite the human scale with the scale of the universe: he would not be satisfied until he fit the microscopic universe into the picture as well.
It should not surprise us that Newton failed. Although he was a firm believer in the existence of atoms, there was no more experimental evidence for their existence than there had been when the ancient Greeks first posited them on purely philosophical grounds. Alchemy labored under a tradition of secrecy and mysticism. Newton had already almost single-handedly transformed the fuzzy-headed field of “natural philosophy” into something we would recognize as the modern science of physics, and it would be unjust to criticize him for failing to change alchemy into modern chemistry as well. The time was not ripe. The microscope was a new invention, and it was cutting-edge science when Newton's contemporary Hooke discovered that living things were made out of cells.
8.1.1 The quest for the atomic force
Newton was not the first of the age of reason. He was the last of the magicians. -- John Maynard Keynes
Newton's quest
Nevertheless it will be instructive to pick up Newton's train of thought and see where it leads us with the benefit of modern hindsight. In uniting the human and cosmic scales of existence, he had reimagined both as stages on which the actors were objects (trees and houses, planets and stars) that interacted through attractions and repulsions. He was already convinced that the objects inhabiting the microworld were atoms, so it remained only to determine what kinds of forces they exerted on each other.
His next insight was no less brilliant for his inability to bring it to fruition. He realized that the many human-scale forces --- friction, sticky forces, the normal forces that keep objects from occupying the same space, and so on --- must all simply be expressions of a more fundamental force acting between atoms. Tape sticks to paper because the atoms in the tape attract the atoms in the paper. My house doesn't fall to the center of the earth because its atoms repel the atoms of the dirt under it.
Here he got stuck. It was tempting to think that the atomic force was a form of gravity, which he knew to be universal, fundamental, and mathematically simple. Gravity, however, is always attractive, so how could he use it to explain the existence of both attractive and repulsive atomic forces? The gravitational force between objects of ordinary size is also extremely small, which is why we never notice cars and houses attracting us gravitationally. It would be hard to understand how gravity could be responsible for anything as vigorous as the beating of a heart or the explosion of gunpowder. Newton went on to write a million words of alchemical notes filled with speculation about some other force, perhaps a “divine force” or “vegetative force” that would for example be carried by the sperm to the egg.
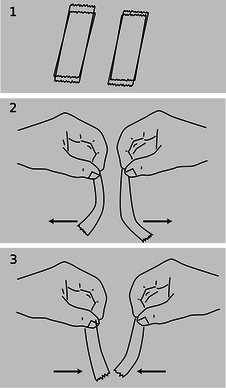
a / Four pieces of tape are prepared, 1, as described in the text. Depending on which combination is tested, the interaction can be either repulsive, 2, or attractive, 3.
Luckily, we now know enough to investigate a different suspect as a candidate for the atomic force: electricity. Electric forces are often observed between objects that have been prepared by rubbing (or other surface interactions), for instance when clothes rub against each other in the dryer. A useful example is shown in figure a/1: stick two pieces of tape on a tabletop, and then put two more pieces on top of them. Lift each pair from the table, and then separate them. The two top pieces will then repel each other, a/2, as will the two bottom pieces. A bottom piece will attract a top piece, however, a/3. Electrical forces like these are similar in certain ways to gravity, the other force that we already know to be fundamental:
- Electrical forces are universal. Although some substances, such as fur, rubber, and plastic, respond more strongly to electrical preparation than others, all matter participates in electrical forces to some degree. There is no such thing as a “nonelectric” substance. Matter is both inherently gravitational and inherently electrical.
- Experiments show that the electrical force, like the gravitational force, is an inverse square force. That is, the electrical force between two spheres is proportional to \(1/r^2\), where \(r\) is the center-to-center distance between them.
Furthermore, electrical forces make more sense than gravity as candidates for the fundamental force between atoms, because we have observed that they can be either attractive or repulsive.
8.1.2 Charge, electricity and magnetism
Charge
“Charge” is the technical term used to indicate that an object has been prepared so as to participate in electrical forces. This is to be distinguished from the common usage, in which the term is used indiscriminately for anything electrical. For example, although we speak colloquially of “charging” a battery, you may easily verify that a battery has no charge in the technical sense, e.g., it does not exert any electrical force on a piece of tape that has been prepared as described in the previous section.
Two types of charge
We can easily collect reams of data on electrical forces between different substances that have been charged in different ways. We find for example that cat fur prepared by rubbing against rabbit fur will attract glass that has been rubbed on silk. How can we make any sense of all this information? A vast simplification is achieved by noting that there are really only two types of charge. Suppose we pick cat fur rubbed on rabbit fur as a representative of type A, and glass rubbed on silk for type B. We will now find that there is no “type C.” Any object electrified by any method is either A-like, attracting things A attracts and repelling those it repels, or B-like, displaying the same attractions and repulsions as B. The two types, A and B, always display opposite interactions. If A displays an attraction with some charged object, then B is guaranteed to undergo repulsion with it, and vice-versa.
The coulomb
Although there are only two types of charge, each type can come in different amounts. The metric unit of charge is the coulomb (rhymes with “drool on”), defined as follows:
One Coulomb (C) is the amount of charge such that a force of \(9.0\times10^9\) N occurs between two point-like objects with charges of 1 C separated by a distance of 1 m.
The notation for an amount of charge is \(q\). The numerical factor in the definition is historical in origin, and is not worth memorizing. The definition is stated for point-like, i.e., very small, objects, because otherwise different parts of them would be at different distances from each other.
A model of two types of charged particles
Experiments show that all the methods of rubbing or otherwise charging objects involve two objects, and both of them end up getting charged. If one object acquires a certain amount of one type of charge, then the other ends up with an equal amount of the other type. Various interpretations of this are possible, but the simplest is that the basic building blocks of matter come in two flavors, one with each type of charge. Rubbing objects together results in the transfer of some of these particles from one object to the other. In this model, an object that has not been electrically prepared may actually possesses a great deal of both types of charge, but the amounts are equal and they are distributed in the same way throughout it. Since type A repels anything that type B attracts, and vice versa, the object will make a total force of zero on any other object. The rest of this chapter fleshes out this model and discusses how these mysterious particles can be understood as being internal parts of atoms.
Use of positive and negative signs for charge
Because the two types of charge tend to cancel out each other's forces, it makes sense to label them using positive and negative signs, and to discuss the total charge of an object. It is entirely arbitrary which type of charge to call negative and which to call positive. Benjamin Franklin decided to describe the one we've been calling “A” as negative, but it really doesn't matter as long as everyone is consistent with everyone else. An object with a total charge of zero (equal amounts of both types) is referred to as electrically \(neutral\).
self-check:
Criticize the following statement: “There are two types of charge, attractive and repulsive.”
(answer in the back of the PDF version of the book)
A large body of experimental observations can be summarized as follows:
Coulomb's law: The magnitude of the force acting between pointlike charged objects at a center-to-center distance \(r\) is given by the equation
where the constant \(k\) equals \(9.0\times10^9\ \text{N}\!\cdot\!\text{m}^2/\text{C}^2\). The force is attractive if the charges are of different signs, and repulsive if they have the same sign.
Clever modern techniques have allowed the \(1/r^2\) form of Coulomb's law to be tested to incredible accuracy, showing that the exponent is in the range from 1.9999999999999998 to 2.0000000000000002.
Note that Coulomb's law is closely analogous to Newton's law of gravity, where the magnitude of the force is \(Gm_1m_2/r^2\), except that there is only one type of mass, not two, and gravitational forces are never repulsive. Because of this close analogy between the two types of forces, we can recycle a great deal of our knowledge of gravitational forces. For instance, there is an electrical equivalent of the shell theorem: the electrical forces exerted externally by a uniformly charged spherical shell are the same as if all the charge was concentrated at its center, and the forces exerted internally are zero.
Conservation of charge
An even more fundamental reason for using positive and negative signs for electrical charge is that experiments show that charge is conserved according to this definition: in any closed system, the total amount of charge is a constant. This is why we observe that rubbing initially uncharged substances together always has the result that one gains a certain amount of one type of charge, while the other acquires an equal amount of the other type. Conservation of charge seems natural in our model in which matter is made of positive and negative particles. If the charge on each particle is a fixed property of that type of particle, and if the particles themselves can be neither created nor destroyed, then conservation of charge is inevitable.
Electrical forces involving neutral objects

b / A charged piece of tape attracts uncharged pieces of paper from a distance, and they leap up to it.
As shown in figure b, an electrically charged object can attract objects that are uncharged. How is this possible? The key is that even though each piece of paper has a total charge of zero, it has at least some charged particles in it that have some freedom to move. Suppose that the tape is positively charged, c. Mobile particles in the paper will respond to the tape's forces, causing one end of the paper to become negatively charged and the other to become positive. The attraction between the paper and the tape is now stronger than the repulsion, because the negatively charged end is closer to the tape.
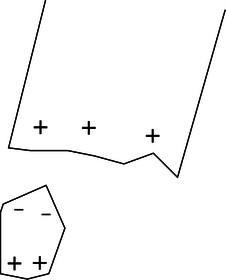
c / The paper has zero total charge, but it does have charged particles in it that can move.
self-check:
What would have happened if the tape was negatively charged? (answer in the back of the PDF version of the book)
The path ahead
We have begun to encounter complex electrical behavior that we would never have realized was occurring just from the evidence of our eyes. Unlike the pulleys, blocks, and inclined planes of mechanics, the actors on the stage of electricity and magnetism are invisible phenomena alien to our everyday experience. For this reason, the flavor of the second half of your physics education is dramatically different, focusing much more on experiments and techniques. Even though you will never actually see charge moving through a wire, you can learn to use an ammeter to measure the flow.
Students also tend to get the impression from their first semester of physics that it is a dead science. Not so! We are about to pick up the historical trail that leads directly to the cutting-edge physics research you read about in the newspaper. The atom-smashing experiments that began around 1900, which we will be studying in this chapter, were not that different from the ones of the year 2000 --- just smaller, simpler, and much cheaper.
Magnetic forces
A detailed mathematical treatment of magnetism won't come until much later in this book, but we need to develop a few simple ideas about magnetism now because magnetic forces are used in the experiments and techniques we come to next. Everyday magnets come in two general types. Permanent magnets, such as the ones on your refrigerator, are made of iron or substances like steel that contain iron atoms. (Certain other substances also work, but iron is the cheapest and most common.) The other type of magnet, an example of which is the ones that make your stereo speakers vibrate, consist of coils of wire through which electric charge flows. Both types of magnets are able to attract iron that has not been magnetically prepared, for instance the door of the refrigerator.
A single insight makes these apparently complex phenomena much simpler to understand: magnetic forces are interactions between moving charges, occurring in addition to the electric forces. Suppose a permanent magnet is brought near a magnet of the coiled-wire type. The coiled wire has moving charges in it because we force charge to flow. The permanent magnet also has moving charges in it, but in this case the charges that naturally swirl around inside the iron. (What makes a magnetized piece of iron different from a block of wood is that the motion of the charge in the wood is random rather than organized.) The moving charges in the coiled-wire magnet exert a force on the moving charges in the permanent magnet, and vice-versa.
The mathematics of magnetism is significantly more complex than the Coulomb force law for electricity, which is why we will wait until chapter 11 before delving deeply into it. Two simple facts will suffice for now:
- If a charged particle is moving in a region of space near where other charged particles are also moving, their magnetic force on it is directly proportional to its velocity.
- The magnetic force on a moving charged particle is always perpendicular to the direction the particle is moving.
| Example 1: A magnetic compass |
|---|
| The Earth is molten inside, and like a pot of boiling water, it roils and churns. To make a drastic oversimplification, electric charge can get carried along with the churning motion, so the Earth contains moving charge. The needle of a magnetic compass is itself a small permanent magnet. The moving charge inside the earth interacts magnetically with the moving charge inside the compass needle, causing the compass needle to twist around and point north. |
| Example 2: A television tube |
|---|
| A TV picture is painted by a stream of electrons coming from the back of the tube to the front. The beam scans across the whole surface of the tube like a reader scanning a page of a book. Magnetic forces are used to steer the beam. As the beam comes from the back of the tube to the front, up-down and left-right forces are needed for steering. But magnetic forces cannot be used to get the beam up to speed in the first place, since they can only push perpendicular to the electrons' direction of motion, not forward along it. |
Discussion Questions
◊ An electrically charged piece of tape will be attracted to your hand. Does that allow us to tell whether the mobile charged particles in your hand are positive or negative, or both?
◊ If the electrical attraction between two pointlike objects at a distance of 1 m is \(9\times10^9\) N, why can't we infer that their charges are \(+1\) and \(-1\) C? What further observations would we need to do in order to prove this?
\[\begin{equation*} \frac{m_\text{Sc}}{m_\text{H}}=44.60 \end{equation*}\]
Examples of masses of atoms compared to that of hydrogen. Note how some, but not all, are close to integers.
8.1.3 Atoms
I was brought up to look at the atom as a nice, hard fellow, red or grey in color according to taste. -- Rutherford
Atomism
The Greeks have been kicked around a lot in the last couple of millennia: dominated by the Romans, bullied during the crusades by warlords going to and from the Holy Land, and occupied by Turkey until recently. It's no wonder they prefer to remember their salad days, when their best thinkers came up with concepts like democracy and atoms. Greece is democratic again after a period of military dictatorship, and an atom is proudly pictured on one of their coins. That's why it hurts me to have to say that the ancient Greek hypothesis that matter is made of atoms was pure guesswork. There was no real experimental evidence for atoms, and the 18th-century revival of the atom concept by Dalton owed little to the Greeks other than the name, which means “unsplittable.” Subtracting even more cruelly from Greek glory, the name was shown to be inappropriate in 1897 when physicist J.J. Thomson proved experimentally that atoms had even smaller things inside them, which could be extracted. (Thomson called them “electrons.”) The “unsplittable” was splittable after all.
But that's getting ahead of our story. What happened to the atom concept in the intervening two thousand years? Educated people continued to discuss the idea, and those who were in favor of it could often use it to give plausible explanations for various facts and phenomena. One fact that was readily explained was conservation of mass. For example, if you mix 1 kg of water with 1 kg of dirt, you get exactly 2 kg of mud, no more and no less. The same is true for the a variety of processes such as freezing of water, fermenting beer, or pulverizing sandstone. If you believed in atoms, conservation of mass made perfect sense, because all these processes could be interpreted as mixing and rearranging atoms, without changing the total number of atoms. Still, this is nothing like a proof that atoms exist.
If atoms did exist, what types of atoms were there, and what distinguished the different types from each other? Was it their sizes, their shapes, their weights, or some other quality? The chasm between the ancient and modern atomisms becomes evident when we consider the wild speculations that existed on these issues until the present century. The ancients decided that there were four types of atoms, earth, water, air and fire; the most popular view was that they were distinguished by their shapes. Water atoms were spherical, hence water's ability to flow smoothly. Fire atoms had sharp points, which was why fire hurt when it touched one's skin. (There was no concept of temperature until thousands of years later.) The drastically different modern understanding of the structure of atoms was achieved in the course of the revolutionary decade stretching 1895 to 1905. The main purpose of this chapter is to describe those momentous experiments.
Atoms, light, and everything else
Although I tend to ridicule ancient Greek philosophers like Aristotle, let's take a moment to praise him for something. If you read Aristotle's writings on physics (or just skim them, which is all I've done), the most striking thing is how careful he is about classifying phenomena and analyzing relationships among phenomena. The human brain seems to naturally make a distinction between two types of physical phenomena: objects and motion of objects. When a phenomenon occurs that does not immediately present itself as one of these, there is a strong tendency to conceptualize it as one or the other, or even to ignore its existence completely. For instance, physics teachers shudder at students' statements that “the dynamite exploded, and force came out of it in all directions.” In these examples, the nonmaterial concept of force is being mentally categorized as if it was a physical substance. The statement that “winding the clock stores motion in the spring” is a miscategorization of electrical energy as a form of motion. An example of ignoring the existence of a phenomenon altogether can be elicited by asking people why we need lamps. The typical response that “the lamp illuminates the room so we can see things,” ignores the necessary role of light coming into our eyes from the things being illuminated.
If you ask someone to tell you briefly about atoms, the likely response is that “everything is made of atoms,” but we've now seen that it's far from obvious which “everything” this statement would properly refer to. For the scientists of the early 1900s who were trying to investigate atoms, this was not a trivial issue of definitions. There was a new gizmo called the vacuum tube, of which the only familiar example today is the picture tube of a TV. In short order, electrical tinkerers had discovered a whole flock of new phenomena that occurred in and around vacuum tubes, and given them picturesque names like “x-rays,” “cathode rays,” “Hertzian waves,” and “N-rays.” These were the types of observations that ended up telling us that we know about matter, but fierce controversies ensued over whether these were themselves forms of matter.
Let's bring ourselves up to the level of classification of phenomena employed by physicists in the year 1900. They recognized three categories:
- Matter has mass, can have kinetic energy, and can travel through a vacuum, transporting its mass and kinetic energy with it. Matter is conserved, both in the sense of conservation of mass and conservation of the number of atoms of each element. Atoms can't occupy the same space as other atoms, so a convenient way to prove something is not a form of matter is to show that it can pass through a solid material, in which the atoms are packed together closely.
- Light has no mass, always has energy, and can travel through a vacuum, transporting its energy with it. Two light beams can penetrate through each other and emerge from the collision without being weakened, deflected, or affected in any other way. Light can penetrate certain kinds of matter, e.g., glass.
- The third category is everything that doesn't fit the definition of light or matter. This catch-all category includes, for example, time, velocity, heat, and force.
The chemical indexelements, chemicalelements
How would one find out what types of atoms there were? Today, it doesn't seem like it should have been very difficult to work out an experimental program to classify the types of atoms. For each type of atom, there should be a corresponding element, i.e., a pure substance made out of nothing but that type of atom. Atoms are supposed to be unsplittable, so a substance like milk could not possibly be elemental, since churning it vigorously causes it to split up into two separate substances: butter and whey. Similarly, rust could not be an element, because it can be made by combining two substances: iron and oxygen. Despite its apparent reasonableness, no such program was carried out until the eighteenth century. The ancients presumably did not do it because observation was not universally agreed on as the right way to answer questions about nature, and also because they lacked the necessary techniques or the techniques were the province of laborers with low social status, such as smiths and miners. Alchemists were hindered by atomism's reputation for subversiveness, and by a tendency toward mysticism and secrecy. (The most celebrated challenge facing the alchemists, that of converting lead into gold, is one we now know to be impossible, since lead and gold are both elements.)
By 1900, however, chemists had done a reasonably good job of finding out what the elements were. They also had determined the ratios of the different atoms' masses fairly accurately. A typical technique would be to measure how many grams of sodium (Na) would combine with one gram of chlorine (Cl) to make salt (NaCl). (This assumes you've already decided based on other evidence that salt consisted of equal numbers of Na and Cl atoms.) The masses of individual atoms, as opposed to the mass ratios, were known only to within a few orders of magnitude based on indirect evidence, and plenty of physicists and chemists denied that individual atoms were anything more than convenient symbols.
Making sense of the elements
As the information accumulated, the challenge was to find a way of systematizing it; the modern scientist's aesthetic sense rebels against complication. This hodgepodge of elements was an embarrassment. One contemporary observer, William Crookes, described the elements as extending “before us as stretched the wide Atlantic before the gaze of Columbus, mocking, taunting and murmuring strange riddles, which no man has yet been able to solve.” It wasn't long before people started recognizing that many atoms' masses were nearly integer multiples of the mass of hydrogen, the lightest element. A few excitable types began speculating that hydrogen was the basic building block, and that the heavier elements were made of clusters of hydrogen. It wasn't long, however, before their parade was rained on by more accurate measurements, which showed that not all of the elements had atomic masses that were near integer multiples of hydrogen, and even the ones that were close to being integer multiples were off by one percent or so.
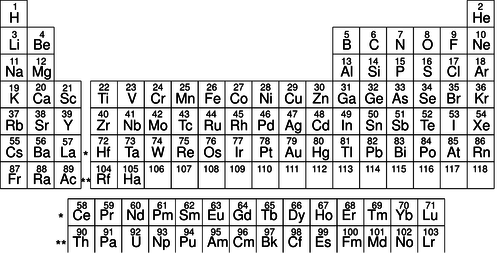
e / A modern periodic table. Elements in the same column have similar chemical properties. The modern atomic numbers, discussed in section 8.2, were not known in Mendeleev's time, since the table could be flipped in various ways.
Chemistry professor Dmitri Mendeleev, preparing his lectures in 1869, wanted to find some way to organize his knowledge for his students to make it more understandable. He wrote the names of all the elements on cards and began arranging them in different ways on his desk, trying to find an arrangement that would make sense of the muddle. The row-and-column scheme he came up with is essentially our modern periodic table. The columns of the modern version represent groups of elements with similar chemical properties, and each row is more massive than the one above it. Going across each row, this almost always resulted in placing the atoms in sequence by weight as well. What made the system significant was its predictive value. There were three places where Mendeleev had to leave gaps in his checkerboard to keep chemically similar elements in the same column. He predicted that elements would exist to fill these gaps, and extrapolated or interpolated from other elements in the same column to predict their numerical properties, such as masses, boiling points, and densities. Mendeleev's professional stock skyrocketed when his three elements (later named gallium, scandium and germanium) were discovered and found to have very nearly the properties he had predicted.
One thing that Mendeleev's table made clear was that mass was not the basic property that distinguished atoms of different elements. To make his table work, he had to deviate from ordering the elements strictly by mass. For instance, iodine atoms are lighter than tellurium, but Mendeleev had to put iodine after tellurium so that it would lie in a column with chemically similar elements.
Direct proof that atoms existed
The success of the kinetic theory of heat was taken as strong evidence that, in addition to the motion of any object as a whole, there is an invisible type of motion all around us: the random motion of atoms within each object. But many conservatives were not convinced that atoms really existed. Nobody had ever seen one, after all. It wasn't until generations after the kinetic theory of heat was developed that it was demonstrated conclusively that atoms really existed and that they participated in continuous motion that never died out.
The smoking gun to prove atoms were more than mathematical abstractions came when some old, obscure observations were reexamined by an unknown Swiss patent clerk named Albert Einstein. A botanist named Brown, using a microscope that was state of the art in 1827, observed tiny grains of pollen in a drop of water on a microscope slide, and found that they jumped around randomly for no apparent reason. Wondering at first if the pollen he'd assumed to be dead was actually alive, he tried looking at particles of soot, and found that the soot particles also moved around. The same results would occur with any small grain or particle suspended in a liquid. The phenomenon came to be referred to as Brownian motion, and its existence was filed away as a quaint and thoroughly unimportant fact, really just a nuisance for the microscopist.
It wasn't until 1906 that Einstein found the correct interpretation for Brown's observation: the water molecules were in continuous random motion, and were colliding with the particle all the time, kicking it in random directions. After all the millennia of speculation about atoms, at last there was solid proof. Einstein's calculations dispelled all doubt, since he was able to make accurate predictions of things like the average distance traveled by the particle in a certain amount of time. (Einstein received the Nobel Prize not for his theory of relativity but for his papers on Brownian motion and the photoelectric effect.)
Discussion Questions
◊ How could knowledge of the size of an individual aluminum atom be used to infer an estimate of its mass, or vice versa?
◊ How could one test Einstein's interpretation of Brownian motion by observing it at different temperatures?
8.1.4 Quantization of charge
Proving that atoms actually existed was a big accomplishment, but demonstrating their existence was different from understanding their properties. Note that the Brown-Einstein observations had nothing at all to do with electricity, and yet we know that matter is inherently electrical, and we have been successful in interpreting certain electrical phenomena in terms of mobile positively and negatively charged particles. Are these particles atoms? Parts of atoms? Particles that are entirely separate from atoms? It is perhaps premature to attempt to answer these questions without any conclusive evidence in favor of the charged-particle model of electricity.

f / A young Robert Millikan. (Contemporary)
Strong support for the charged-particle model came from a 1911 experiment by physicist Robert Millikan at the University of Chicago. Consider a jet of droplets of perfume or some other liquid made by blowing it through a tiny pinhole. The droplets emerging from the pinhole must be smaller than the pinhole, and in fact most of them are even more microscopic than that, since the turbulent flow of air tends to break them up. Millikan reasoned that the droplets would acquire a little bit of electric charge as they rubbed against the channel through which they emerged, and if the charged-particle model of electricity was right, the charge might be split up among so many minuscule liquid drops that a single drop might have a total charge amounting to an excess of only a few charged particles --- perhaps an excess of one positive particle on a certain drop, or an excess of two negative ones on another.
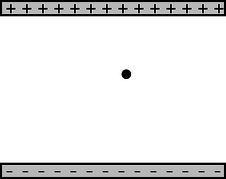
g / A simplified diagram of Millikan's apparatus.
Millikan's ingenious apparatus, g, consisted of two metal plates, which could be electrically charged as needed. He sprayed a cloud of oil droplets into the space between the plates, and selected one drop through a microscope for study. First, with no charge on the plates, he would determine the drop's mass by letting it fall through the air and measuring its terminal velocity, i.e., the velocity at which the force of air friction canceled out the force of gravity. The force of air drag on a slowly moving sphere had already been found by experiment to be \(bvr^2\), where \(b\) was a constant. Setting the total force equal to zero when the drop is at terminal velocity gives
and setting the known density of oil equal to the drop's mass divided by its volume gives a second equation,
Everything in these equations can be measured directly except for \(m\) and \(r\), so these are two equations in two unknowns, which can be solved in order to determine how big the drop is.
Next Millikan charged the metal plates, adjusting the amount of charge so as to exactly counteract gravity and levitate the drop. If, for instance, the drop being examined happened to have a total charge that was negative, then positive charge put on the top plate would attract it, pulling it up, and negative charge on the bottom plate would repel it, pushing it up. (Theoretically only one plate would be necessary, but in practice a two-plate arrangement like this gave electrical forces that were more uniform in strength throughout the space where the oil drops were.) The amount of charge on the plates required to levitate the charged drop gave Millikan a handle on the amount of charge the drop carried. The more charge the drop had, the stronger the electrical forces on it would be, and the less charge would have to be put on the plates to do the trick. Unfortunately, expressing this relationship using Coulomb's law would have been impractical, because it would require a perfect knowledge of how the charge was distributed on each plate, plus the ability to perform vector addition of all the forces being exerted on the drop by all the charges on the plate. Instead, Millikan made use of the fact that the electrical force experienced by a pointlike charged object at a certain point in space is proportional to its charge,
With a given amount of charge on the plates, this constant could be determined for instance by discarding the oil drop, inserting between the plates a larger and more easily handled object with a known charge on it, and measuring the force with conventional methods. (Millikan actually used a slightly different set of techniques for determining the constant, but the concept is the same.) The amount of force on the actual oil drop had to equal \(mg\), since it was just enough to levitate it, and once the calibration constant had been determined, the charge of the drop could then be found based on its previously determined mass.
| q (C) | q / (1.64 X 10-19 C) |
| − 1.970×10 − 18 | − 12.02 |
| − 0.987×10 − 18 | − 6.02 |
| − 2.773×10 − 18 | − 16.93 |
A few samples of Millikan's data.
The table above shows a few of the results from Millikan's 1911 paper. (Millikan took data on both negatively and positively charged drops, but in his paper he gave only a sample of his data on negatively charged drops, so these numbers are all negative.) Even a quick look at the data leads to the suspicion that the charges are not simply a series of random numbers. For instance, the second charge is almost exactly equal to half the first one. Millikan explained the observed charges as all being integer multiples of a single number, \(1.64\times10^{-19}\) C. In the second column, dividing by this constant gives numbers that are essentially integers, allowing for the random errors present in the experiment. Millikan states in his paper that these results were a
... direct and tangible demonstration ... of the correctness of the view advanced many years ago and supported by evidence from many sources that all electrical charges, however produced, are exact multiples of one definite, elementary electrical charge, or in other words, that an electrical charge instead of being spread uniformly over the charged surface has a definite granular structure, consisting, in fact, of ... specks, or atoms of electricity, all precisely alike, peppered over the surface of the charged body.
In other words, he had provided direct evidence for the charged-particle model of electricity and against models in which electricity was described as some sort of fluid. The basic charge is notated \(e\), and the modern value is \(e=1.60\times10^{-19}\) C. The word “quantized” is used in physics to describe a quantity that can only have certain numerical values, and cannot have any of the values between those. In this language, we would say that Millikan discovered that charge is quantized. The charge \(e\) is referred to as the quantum of charge.
A historical note on Millikan's fraud
Very few undergraduate physics textbooks mention the well-documented fact that although Millikan's conclusions were correct, he was guilty of scientific fraud. His technique was difficult and painstaking to perform, and his original notebooks, which have been preserved, show that the data were far less perfect than he claimed in his published scientific papers. In his publications, he stated categorically that every single oil drop observed had had a charge that was a multiple of \(e\), with no exceptions or omissions. But his notebooks are replete with notations such as “beautiful data, keep,” and “bad run, throw out.” Millikan, then, appears to have earned his Nobel Prize by advocating a correct position with dishonest descriptions of his data.
Why do textbook authors fail to mention Millikan's fraud? It may be that they think students are too unsophisticated to correctly evaluate the implications of the fact that scientific fraud has sometimes existed and even been rewarded by the scientific establishment. Maybe they are afraid students will reason that fudging data is OK, since Millikan got the Nobel Prize for it. But falsifying history in the name of encouraging truthfulness is more than a little ironic. English teachers don't edit Shakespeare's tragedies so that the bad characters are always punished and the good ones never suffer!
self-check:
Is money quantized? What is the quantum of money?
(answer in the back of the PDF version of the book)
8.1.5 The electron
Cathode Rays
Nineteenth-century physicists spent a lot of time trying to come up with wild, random ways to play with electricity. The best experiments of this kind were the ones that made big sparks or pretty colors of light.
One such parlor trick was the cathode ray. To produce it, you first had to hire a good glassblower and find a good vacuum pump. The glassblower would create a hollow tube and embed two pieces of metal in it, called the electrodes, which were connected to the outside via metal wires passing through the glass. Before letting him seal up the whole tube, you would hook it up to a vacuum pump, and spend several hours huffing and puffing away at the pump's hand crank to get a good vacuum inside. Then, while you were still pumping on the tube, the glassblower would melt the glass and seal the whole thing shut. Finally, you would put a large amount of positive charge on one wire and a large amount of negative charge on the other. Metals have the property of letting charge move through them easily, so the charge deposited on one of the wires would quickly spread out because of the repulsion of each part of it for every other part. This spreading-out process would result in nearly all the charge ending up in the electrodes, where there is more room to spread out than there is in the wire. For obscure historical reasons a negative electrode is called a cathode and a positive one is an anode.
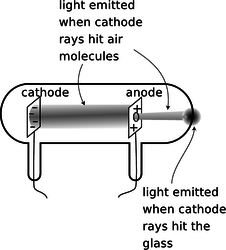
i / Cathode rays observed in a vacuum tube.
Figure i shows the light-emitting stream that was observed. If, as shown in this figure, a hole was made in the anode, the beam would extend on through the hole until it hit the glass. Drilling a hole in the cathode, however would not result in any beam coming out on the left side, and this indicated that the stuff, whatever it was, was coming from the cathode. The rays were therefore christened “cathode rays.” (The terminology is still used today in the term “cathode ray tube” or “CRT” for the picture tube of a TV or computer monitor.)
Were cathode rays a form of light, or of matter?
Were cathode rays a form of light, or matter? At first no one really cared what they were, but as their scientific importance became more apparent, the light-versus-matter issue turned into a controversy along nationalistic lines, with the Germans advocating light and the English holding out for matter. The supporters of the material interpretation imagined the rays as consisting of a stream of atoms ripped from the substance of the cathode.
One of our defining characteristics of matter is that material objects cannot pass through each other. Experiments showed that cathode rays could penetrate at least some small thickness of matter, such as a metal foil a tenth of a millimeter thick, implying that they were a form of light.
Other experiments, however, pointed to the contrary conclusion. Light is a wave phenomenon, and one distinguishing property of waves is demonstrated by speaking into one end of a paper towel roll. The sound waves do not emerge from the other end of the tube as a focused beam. Instead, they begin spreading out in all directions as soon as they emerge. This shows that waves do not necessarily travel in straight lines. If a piece of metal foil in the shape of a star or a cross was placed in the way of the cathode ray, then a “shadow” of the same shape would appear on the glass, showing that the rays traveled in straight lines. This straight-line motion suggested that they were a stream of small particles of matter.
These observations were inconclusive, so what was really needed was a determination of whether the rays had mass and weight. The trouble was that cathode rays could not simply be collected in a cup and put on a scale. When the cathode ray tube is in operation, one does not observe any loss of material from the cathode, or any crust being deposited on the anode.
Nobody could think of a good way to weigh cathode rays, so the next most obvious way of settling the light/matter debate was to check whether the cathode rays possessed electrical charge. Light was known to be uncharged. If the cathode rays carried charge, they were definitely matter and not light, and they were presumably being made to jump the gap by the simultaneous repulsion of the negative charge in the cathode and attraction of the positive charge in the anode. The rays would overshoot the anode because of their momentum. (Although electrically charged particles do not normally leap across a gap of vacuum, very large amounts of charge were being used, so the forces were unusually intense.)
Thomson's experiments

j / J.J. Thomson in the lab.
Physicist J.J. Thomson at Cambridge carried out a series of definitive experiments on cathode rays around the year 1897. By turning them slightly off course with electrical forces, k, he showed that they were indeed electrically charged, which was strong evidence that they were material. Not only that, but he proved that they had mass, and measured the ratio of their mass to their charge, \(m/q\). Since their mass was not zero, he concluded that they were a form of matter, and presumably made up of a stream of microscopic, negatively charged particles. When Millikan published his results fourteen years later, it was reasonable to assume that the charge of one such particle equaled minus one fundamental charge, \(q=-e\), and from the combination of Thomson's and Millikan's results one could therefore determine the mass of a single cathode ray particle.
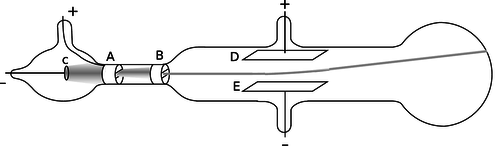
k / Thomson's experiment proving cathode rays had electric charge (redrawn from his original paper). The cathode, C, and anode, A, are as in any cathode ray tube. The rays pass through a slit in the anode, and a second slit, B, is interposed in order to make the beam thinner and eliminate rays that were not going straight. Charging plates D and E shows that cathode rays have charge: they are attracted toward the positive plate D and repelled by the negative plate E.
The basic technique for determining \(m/q\) was simply to measure the angle through which the charged plates bent the beam. The electric force acting on a cathode ray particle while it was between the plates would be proportional to its charge,
Application of Newton's second law, \(a=F/m\), would allow \(m/q\) to be determined:
There was just one catch. Thomson needed to know the cathode ray particles' velocity in order to figure out their acceleration. At that point, however, nobody had even an educated guess as to the speed of the cathode rays produced in a given vacuum tube. The beam appeared to leap across the vacuum tube practically instantaneously, so it was no simple matter of timing it with a stopwatch!
Thomson's clever solution was to observe the effect of both electric and magnetic forces on the beam. The magnetic force exerted by a particular magnet would depend on both the cathode ray's charge and its velocity:
Thomson played with the electric and magnetic forces until either one would produce an equal effect on the beam, allowing him to solve for the velocity,
Knowing the velocity (which was on the order of 10% of the speed of light for his setup), he was able to find the acceleration and thus the mass-to-charge ratio \(m/q\). Thomson's techniques were relatively crude (or perhaps more charitably we could say that they stretched the state of the art of the time), so with various methods he came up with \(m/q\) values that ranged over about a factor of two, even for cathode rays extracted from a cathode made of a single material. The best modern value is \(m/q=5.69\times10^{-12}\) kg/C, which is consistent with the low end of Thomson's range.
The cathode ray as a subatomic particle: the indexelectronelectron
What was significant about Thomson's experiment was not the actual numerical value of \(m/q\), however, so much as the fact that, combined with Millikan's value of the fundamental charge, it gave a mass for the cathode ray particles that was thousands of times smaller than the mass of even the lightest atoms. Even without Millikan's results, which were 14 years in the future, Thomson recognized that the cathode rays' \(m/q\) was thousands of times smaller than the \(m/q\) ratios that had been measured for electrically charged atoms in chemical solutions. He correctly interpreted this as evidence that the cathode rays were smaller building blocks --- he called them electrons --- out of which atoms themselves were formed. This was an extremely radical claim, coming at a time when atoms had not yet been proven to exist! Even those who used the word “atom” often considered them no more than mathematical abstractions, not literal objects. The idea of searching for structure inside of “unsplittable” atoms was seen by some as lunacy, but within ten years Thomson's ideas had been amply verified by many more detailed experiments.
Discussion Questions
◊ Thomson started to become convinced during his experiments that the “cathode rays” observed coming from the cathodes of vacuum tubes were building blocks of atoms --- what we now call electrons. He then carried out observations with cathodes made of a variety of metals, and found that \(m/q\) was roughly the same in every case, considering his limited accuracy. Given his suspicion, why did it make sense to try different metals? How would the consistent values of \(m/q\) serve to test his hypothesis?
◊ My students have frequently asked whether the \(m/q\) that Thomson measured was the value for a single electron, or for the whole beam. Can you answer this question?
◊ Thomson found that the \(m/q\) of an electron was thousands of times smaller than that of charged atoms in chemical solutions. Would this imply that the electrons had more charge? Less mass? Would there be no way to tell? Explain. Remember that Millikan's results were still many years in the future, so \(q\) was unknown.
◊ Can you guess any practical reason why Thomson couldn't just let one electron fly across the gap before disconnecting the battery and turning off the beam, and then measure the amount of charge deposited on the anode, thus allowing him to measure the charge of a single electron directly?
◊ Why is it not possible to determine \(m\) and \(q\) themselves, rather than just their ratio, by observing electrons' motion in electric and magnetic fields?
8.1.6 The raisin cookie model of the atom
Based on his experiments, Thomson proposed a picture of the atom which became known as the raisin cookie model. In the neutral atom, l, there are four electrons with a total charge of \(-4e\), sitting in a sphere (the “cookie”) with a charge of \(+4e\) spread throughout it. It was known that chemical reactions could not change one element into another, so in Thomson's scenario, each element's cookie sphere had a permanently fixed radius, mass, and positive charge, different from those of other elements. The electrons, however, were not a permanent feature of the atom, and could be tacked on or pulled out to make charged ions. Although we now know, for instance, that a neutral atom with four electrons is the element beryllium, scientists at the time did not know how many electrons the various neutral atoms possessed.
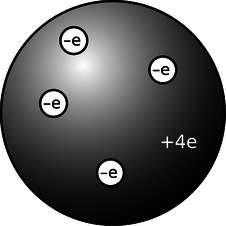
l / The raisin cookie model of the atom with four units of charge, which we now know to be beryllium.
This model is clearly different from the one you've learned in grade school or through popular culture, where the positive charge is concentrated in a tiny nucleus at the atom's center. An equally important change in ideas about the atom has been the realization that atoms and their constituent subatomic particles behave entirely differently from objects on the human scale. For instance, we'll see later that an electron can be in more than one place at one time. The raisin cookie model was part of a long tradition of attempts to make mechanical models of phenomena, and Thomson and his contemporaries never questioned the appropriateness of building a mental model of an atom as a machine with little parts inside. Today, mechanical models of atoms are still used (for instance the tinker-toy-style molecular modeling kits like the ones used by Watson and Crick to figure out the double helix structure of DNA), but scientists realize that the physical objects are only aids to help our brains' symbolic and visual processes think about atoms.
Although there was no clear-cut experimental evidence for many of the details of the raisin cookie model, physicists went ahead and started working out its implications. For instance, suppose you had a four-electron atom. All four electrons would be repelling each other, but they would also all be attracted toward the center of the “cookie” sphere. The result should be some kind of stable, symmetric arrangement in which all the forces canceled out. People sufficiently clever with math soon showed that the electrons in a four-electron atom should settle down at the vertices of a pyramid with one less side than the Egyptian kind, i.e., a regular tetrahedron. This deduction turns out to be wrong because it was based on incorrect features of the model, but the model also had many successes, a few of which we will now discuss.
| Example 3: Flow of electrical charge in wires |
|---|
| One of my former students was the son of an electrician, and had become an electrician himself. He related to me how his father had remained refused to believe all his life that electrons really flowed through wires. If they had, he reasoned, the metal would have gradually become more and more damaged, eventually crumbling to dust. His opinion is not at all unreasonable based on the fact that electrons are material particles, and that matter cannot normally pass through matter without making a hole through it. Nineteenth-century physicists would have shared his objection to a charged-particle model of the flow of electrical charge. In the raisin-cookie model, however, the electrons are very low in mass, and therefore presumably very small in size as well. It is not surprising that they can slip between the atoms without damaging them. |
| Example 4: Flow of electrical charge across cell membranes |
|---|
| Your nervous system is based on signals carried by charge moving from nerve cell to nerve cell. Your body is essentially all liquid, and atoms in a liquid are mobile. This means that, unlike the case of charge flowing in a solid wire, entire charged atoms can flow in your nervous system |
| Example 5: Emission of electrons in a cathode ray tube |
|---|
| Why do electrons detach themselves from the cathode of a vacuum tube? Certainly they are encouraged to do so by the repulsion of the negative charge placed on the cathode and the attraction from the net positive charge of the anode, but these are not strong enough to rip electrons out of atoms by main force --- if they were, then the entire apparatus would have been instantly vaporized as every atom was simultaneously ripped apart! The raisin cookie model leads to a simple explanation. We know that heat is the energy of random motion of atoms. The atoms in any object are therefore violently jostling each other all the time, and a few of these collisions are violent enough to knock electrons out of atoms. If this occurs near the surface of a solid object, the electron may can come loose. Ordinarily, however, this loss of electrons is a self-limiting process; the loss of electrons leaves the object with a net positive charge, which attracts the lost sheep home to the fold. (For objects immersed in air rather than vacuum, there will also be a balanced exchange of electrons between the air and the object.) This interpretation explains the warm and friendly yellow glow of the vacuum tubes in an antique radio. To encourage the emission of electrons from the vacuum tubes' cathodes, the cathodes are intentionally warmed up with little heater coils. |
Discussion Questions
◊ Today many people would define an ion as an atom (or molecule) with missing electrons or extra electrons added on. How would people have defined the word “ion” before the discovery of the electron?
◊ Since electrically neutral atoms were known to exist, there had to be positively charged subatomic stuff to cancel out the negatively charged electrons in an atom. Based on the state of knowledge immediately after the Millikan and Thomson experiments, was it possible that the positively charged stuff had an unquantized amount of charge? Could it be quantized in units of +e? In units of +2e? In units of +5/7e?
Contributor
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


