1.8: Length Contraction and the Magnetic Force (Project)
( \newcommand{\kernel}{\mathrm{null}\,}\)
As I’m sure you recall, the magnetic force between a charged particle and a current-carrying wire depends on whether the particle is moving. If the particle is stationary, no magnetic force is present. However, if the particle moves, a magnetic force acts on the particle. Of course, whether something is moving or not depends on the frame of reference of the observer, i.e., motion is a purely relative concept. Does that mean that the magnetic force, and possibly the magnetic field, have no absolute, frame-independent existence and are also purely relative concepts? If so, perhaps the effects of magnetism can be explained in terms of some more fundamental concepts.
Imagine a current-carrying wire, illustrated below in the laboratory frame of reference. The average separation between the stationary positive nuclei is L+o. Note that this is a proper length for the separation between positive charges. The negative charges are moving at speed v and have an average separation L− in the laboratory frame. A stationary negative charge is a distance, r, to the right of the wire.
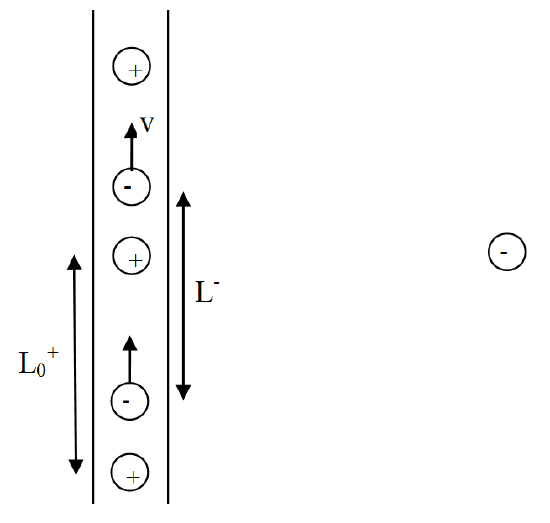
I. Charge Density in the Laboratory Frame
The total electric charge density on the wire λ, is the sum of the positive and negative charge densities. The positive charge density is simply the ratio of the positive charge, +e, over the separation between positive charges, L+o.
1. Write an expression for the total electric charge density on the wire, λ.
2. Since current-carrying wires are electrically neutral, this density must equal zero. Based on this observation, what is the relationship between L+o and L−?
Obviously, there is no electric or magnetic force on the particle for this scenario. Boring. So let’s imagine the particle moving with the same speed and direction as the current-carrying electrons.
3. What is the direction of the magnetic field from the current-carrying wire at the location of the moving particle?
4. What is the direction of the magnetic force on the moving particle?
(You should get the same direction for the magnetic force on the moving particle if you consider the wire and particle as two parallel currents flowing in the same direction.)
5. Using the result for the magnetic field from a long wire carrying current i, write an expression for the magnitude of the magnetic force acting on the moving particle.
II. Charge Density in the Moving Particle Frame
Let’s see what’s happening in the frame of reference of the moving particle. Note that in this frame of reference, the positive nuclei are moving “backward” with speed v and the electrons in the wire are at rest.
A. Conceptual Comparison
1. As you move from the laboratory frame into the moving particle frame, what happens to the separation between the electrons in the wire (i.e., does it stay the same, become larger, or become smaller)?
2. As you move from the laboratory frame into the moving particle frame, what happens to the separation between the positive nuclei in the wire (i.e., does it stay the same, become larger, or become smaller)?
3. Therefore, as you move from the laboratory frame into the moving particle frame, what happens to the electric charge density on the wire (i.e., does it stay neutral, become positive, or become negative)?
4. Based on the electric charge density on the wire, what is the direction of the electric force on the moving particle?
It appears that due to relativistic length contraction the neutral (in the laboratory frame) wire is positively charged in the moving particle frame and attracts the moving particle electrically. Could it be that what we have called the magnetic force is really simply the electric force from a length contracted charge distribution? To prove this conjecture we are going to have to get quantitative.
B. Quantitative Comparison
1. Write an expression for the total electric charge density on the wire in the moving frame λ′. Clearly designate whether a separation is a proper length (Lo) or not (L).
2. Using the length contraction relationship, replace the separation between electrons in this frame with the separation between electrons in the laboratory frame (L−).
3. Using your result from I.2., replace L− in your expression.
4. Using the length contraction relationship, replace the proper separation between nuclei (L+o) with the separation in the moving particle frame.
5. Factor out the common term in your expression and simplify. Your final result should be in terms of e, L+, v and c only, and should be clearly a positive value.
6. Using Gauss’ Law (or looking in your old notes), determine the electric field a distance r from a wire with linear charge density λ′.
7. Based on this electric field, write an expression for the electric force acting on the moving charge.
If we can show that this expression is exactly the same as the “magnetic” force acting on the moving charge, we will have shown that what we have traditionally called magnetic force is really simply the electric force from a length-contracted charge distribution.
8. Current is defined as the product of a charge density and a velocity. Write an expression for the current in the moving frame, i’. (Note, only the positive nuclei are moving in this frame so only their charge density contributes to the current.)
9. Using this result, replace the charge density (’) in your electric force expression with current (i').
10. Using
c=1√ϵoμo
show that your expression for electric force is identical to the expression for magnetic force in I.5.
C. Summary
So, what does this all mean? Basically, certain objects that are neutral in one frame of reference are actually electrically charged in other frames of reference due to length contraction. Moving charges (and hence electric currents) see these “charged-because-of-length-contraction” objects and feel electric forces of either attraction or repulsion. However, in our frame the objects are neutral so we “invent” a new force, magnetism, to make sense of the behavior of these moving charges. Now that we understand length contraction, there really is no need to think of the magnetic force as being different from the electric force. (It’s often more convenient to talk about magnetism, but it’s never really necessary.) Although it may be hard to believe, the pictures attached to your refrigerator are held in place because of relativistic length contraction!
What’s really strange, however, is how small of a length contraction is responsible for this effect. Most people have the idea that current-carrying electrons are “zipping” through a wire at high speeds. However, the average speed of an electron in a current-carrying wire (the drift speed) is typically only a couple millimeters per second! Electrons moving at this tiny speed experience ridiculously small length contractions, on the order of one part in 1022! This tiny amount of “shrinkage” gives rise to the measurable forces of magnetism because of the incredible strength of the electric force. Basically, the electric force is so strong that even this little bit of shrinking gives rise to a tiny amount of net charge that results in a force large enough to notice with the naked eye. Or to hold a photo on a refrigerator.


