7.A: Relativistic Baseball (Project)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Text and drawings from: https://what-if.xkcd.com/1/
What would happen if you tried to hit a baseball pitched at 90% the speed of light? - Ellen McManis
Let’s set aside the question of how we got the baseball moving that fast. We'll suppose it's a normal pitch, except in the instant the pitcher releases the ball, it magically accelerates to 0.9c. From that point onward, everything proceeds according to normal physics:
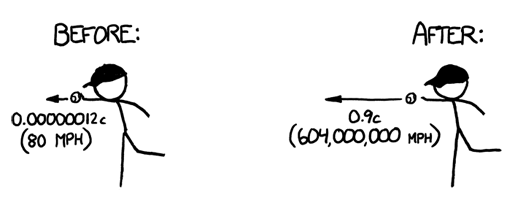
The answer turns out to be “a lot of things”, and they all happen very quickly, and it doesn’t end well for the batter (or the pitcher). I sat down with some physics books, a Nolan Ryan action figure, and a bunch of videotapes of nuclear tests and tried to sort it all out. What follows is my best guess at a nanosecond-by-nanosecond portrait:
The ball is going so fast that everything else is practically stationary. Even the molecules in the air are stationary. Air molecules vibrate back and forth at a few hundred miles per hour, but the ball is moving through them at 600 million miles per hour. This means that as far as the ball is concerned, they’re just hanging there, frozen.
Q1
Find the total mass of air and the total number of air molecules struck by the ball on its way to the plate. How many of these molecules are N2 and how many are O2? (Obviously, you are going to need to find out some basic parameters about baseballs and air.)
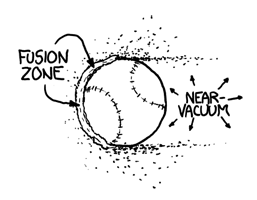
The ideas of aerodynamics don’t apply here. Normally, air would flow around anything moving through it. But the air molecules in front of this ball don’t have time to be jostled out of the way. The ball smacks into them so hard that the atoms in the air molecules actually fuse with the atoms in the ball’s surface. Each collision releases a burst of gamma rays and scattered particles.
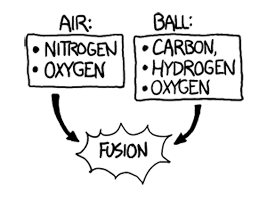
Q2
Calculate plausible reactions and Q’s for the fusion of the air with the carbon of the ball.
These gamma rays and debris expand outward in a bubble centered on the pitcher’s mound. They start to tear apart the molecules in the air, ripping the electrons from the nuclei and turning the air in the stadium into an expanding bubble of incandescent plasma. The wall of this bubble approaches the batter at about the speed of light—only slightly ahead of the ball itself.
The constant fusion at the front of the ball pushes back on it, slowing it down, as if the ball were a rocket flying tail-first while firing its engines. Unfortunately, the ball is going so fast that even the tremendous force from this ongoing thermonuclear explosion barely slows it down at all. It does, however, start to eat away at the surface, blasting tiny particulate fragments of the ball in all directions. These fragments are going so fast that when they hit air molecules, they trigger two or three more rounds of fusion.
Q3
Using momentum conservation, and ignoring the change in mass of the ball due to ablation, analyze the collision of the ball and the air molecules as a simple, inelastic collision (i.e., the air sticks to the ball). Find the speed of the ball as it crosses home plate. (Hint: You know the total mass of air that “sticks’ to the ball from question 1.)
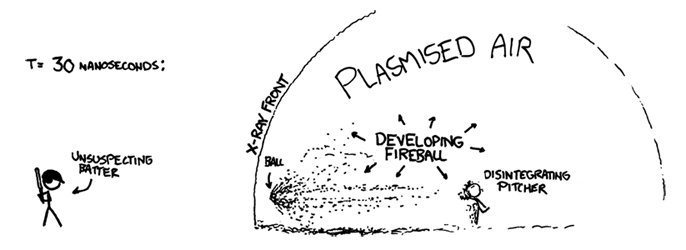
After about 70 nanoseconds the ball arrives at home plate. The batter hasn't even seen the pitcher let go of the ball, since the light carrying that information arrives at about the same time the ball does.
Q4
Find the difference in arrival times between the light and the ball, ignoring the deceleration of the ball. This is the amount of time you would have to react and swing (assuming it’s a strike). (It normally takes about 30 ms to react to a visual stimulus.)
Collisions with the air have eaten the ball away almost completely, and it is now a bullet-shaped cloud of expanding plasma (mainly carbon, oxygen, hydrogen, and nitrogen) ramming into the air and triggering more fusion as it goes. The shell of x-rays hits the batter first, and a handful of nanoseconds later the debris cloud hits.
When it reaches the batter, the center of the cloud is still moving at an appreciable fraction of the speed of light. It hits the bat first, but then the batter, plate, and catcher are all scooped up and carried backward through the backstop as they disintegrate. The shell of x-rays and superheated plasma expands outward and upward, swallowing the backstop, both teams, the stands, and the surrounding neighborhood—all in the first microsecond.
Suppose you’re watching from a hilltop outside the city. The first thing you see is a blinding light, far outshining the sun. This gradually fades over the course of a few seconds, and a growing fireball rises into a mushroom cloud. Then, with a great roar, the blast wave arrives, tearing up trees and shredding houses.
Everything within roughly a mile of the park is leveled, and a firestorm engulfs the surrounding city. The baseball diamond is now a sizable crater, centered a few hundred feet behind the former location of the backstop.
Q5
Based on your Q’s from question 2, and the number of collisions from question 1, estimate the total energy released by fusion. (Assume all of the air molecules undergo fusion with carbon.) (For comparison, the total energy released by the Hiroshima bomb was about 60×1012J, and it leveled approximately 5 square miles.)

A careful reading of official Major League Baseball Rule 6.08(b) suggests that in this situation, the batter would be considered "hit by pitch", and would be eligible to advance to first base.


