6.5: The Doppler Shift and Aberration
- Page ID
- 3456
Learning Objectives
- What is aberration
Doppler Shifts
As an example, we generalize our previous discussion of the Doppler shift of light to \(3 + 1\) dimensions.
For clarity, let’s first show how the \(1+1\)-dimensional case works in our new notation. For a wave traveling to the left, we have \(ω\to = (ω,ω)\) (not \((ω,-ω)\) — see figure 6.6.1 (1). We now want to transform into the frame of an observer moving to the right with velocity \(v\) relative to the original frame. Because \(ω\to \) is a covector, we do this using the inverse Lorentz transformation. An ordinary Lorentz transformation would take a lightlike vector \((ω,ω)\) to \((ω/D,ω/D)\) (see section 3.2). The inverse Lorentz transformation gives \((Dω,Dω)\). The frequency has been shifted upward by the factor \(D\), as established previously.
In \(3 + 1\) dimensions, a spatial plane is determined by the light’s direction of propagation and the relative velocity of the source and observer, so this case reduces without loss of generality to \(2 + 1\) dimensions. The frequency four-vector must be lightlike, so its most general possible form is \((ω,ω cosθ,ω sinθ)\), where \(θ\) is interpreted as the angle between the direction of propagation and the relative velocity. In \(2+1\) dimensions, a Lorentz boost along the \(x\)- axis looks like this:
\[t' = \gamma t - v\gamma x\]
\[x' = - v\gamma t + \gamma x\]
\[y' = y\]
The inverse transformation is found by flipping the sign of \(v\). Putting our frequency vector through an inverse Lorentz boost, we find
\[\omega ' = \gamma \omega (1 + v\cos \theta )\]
For \(θ = 0\) the Doppler factor reduces to
\[γ(1+v) = D\]
which recovers the \(1 + 1\)-dimensional result. For \(\theta = 90^{\circ}\), we have \(ω' = γω\), which is interpreted as a pure time dilation effect when the source’s motion is transverse to the line of sight.
To see the power of the mathematical tools we’ve developed in this chapter, you may wish to look at sections 6 and 7 of Einstein’s 1905 paper on special relativity, where a lengthy derivation is needed in order to arrive at the same result.
Aberration
Imagine that rain is falling vertically while you drive in a convertible with the top down. To you, the raindrops appear to be moving at some nonzero angle relative to vertical. This is referred to as aberration.
Definition: aberration
A world-line’s direction changes depending on one’s frame of reference.
In the street’s frame of reference, the angle between the rain’s three-velocity and the car’s is \(\theta = 90^{\circ}\), but in the car’s frame \(\theta ' \neq 90^{\circ}\). In this example, aberration is a large effect because the car’s speed \(v\) is comparable to the velocity \(u\) of the raindrops. To a snail crawling along the sidewalk at a much lower \(v\), the effect would be small. Using the small-angle approximation \(\tan \epsilon \approx \epsilon\), we find that for small \(v\), the difference \(∆θ = θ' - θ\) would be approximately \(v/u\), in units of radians.
Compared to a ray of light, we’re all like snails. For example, the earth’s orbital speed is about \(v ∼ 10^{-4}\) in units where the speed of light \(u = 1\), so we expect a maximum effect of about \(10^{-4}\) radians, or \(2'' \) of arc, which is small but not negligible for a telescope with a high-quality mount, being used at high magnification.
This estimate of astronomical aberration of light is roughly right, but we don’t expect it to be exact, both because of the small-angle approximation and because we calculated it using a Galilean picture of spacetime. Let’s calculate the exact result. As shown in Example 6.6.1, the direction of propagation of a light wave lies along the vector that is the dual to its frequency covector. Let’s call this direction of propagation \(\to u\). Reusing the expression for \(ω\to \) defined above, and arbitrarily fixing \(\to u\)’s timelike component to be \(1\), we have
\[\to u = (1,-\cos\theta ,-\sin\theta )\]
When this vector undergoes a boost \(v\) along the \(x\)- axis it becomes
\[\to u' = \left ( \gamma (1 + v\cos \theta ), \gamma (-v - v\cos \theta ), -\sin \theta \right )\]
The original angle
\[\theta = \tan^{-1}\frac{u_y}{u_x}\]
has been transformed to
\[\theta ' = \tan^{-1}\frac{u_y'}{u_x'}\]
the result being
\[\tan \theta ' = \frac{\sin \theta }{\gamma (\cos \theta + v)}\]
Example \(\PageIndex{1}\): A test of special relativity
An assumption underlying this treatment of aberration was that the speed of light was \(u = c\), regardless of the velocity of the source. Not all prerelativistic theories had this property, and one would expect that in such a theory, aberration would not be in accord with the relativistic result. In particular, suppose that we believed in Galilean spacetime, so that when a distant galaxy, receding from us at some speed \(w\), emitted a ray of light toward us, the light’s velocity in our frame was \(u = c - w\). That is, we imagine a theory in which emitting a ray of light is like shooting a bullet from a gun. Since aberration effects go approximately like \(v/u\), we would expect that the reduced \(u\) would lead to more aberration compared to the prediction of relativity.
To test theories of this type, Heckmann1 used a \(24\)-inch reflector at Hamburg to take high-magnification photographic plates of a star field in Ursa Major containing \(11\) stars inside the Milky Way and \(5\) distant galaxies. Measurements of Doppler shifts showed that the galaxies were receding from us at velocities of about \(w = 0.05c\), whereas stars within the Milky Way move relative to us at speeds that are negligible in comparison. If, contrary to the relativistic prediction, this led to a \(5\%\) decrease in \(u\), then we would expect about a \(5\%\) increase in aberration for the galaxies compared to the stars.
Over the course of a year, the earth’s orbit carries it toward and away from Ursa Major, so that in the earth’s frame of reference, the stars and galaxies have varying velocities relative to us, and the \(∼20''\) aberration effect oscillates in direction. If the effect was different for the galaxies and the stars, then they ought to shift their apparent positions relative to one another. The shift ought to be on the order of \(5\%\) of \(2000\), or one second of arc. The results from the observations showed that these relative positions did not appear to vary at all over the course of a year, with the average relative shift being \(0.00±0.06''\) of arc. This difference in aberration is consistent with zero, as predicted by special relativity.
Example \(\PageIndex{2}\): The view of an ultrarelativistic observer
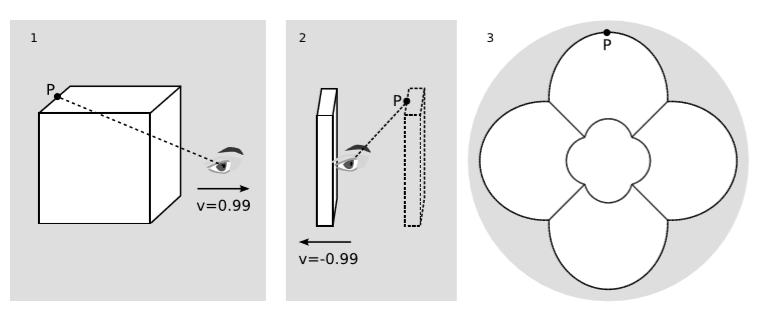
Figure \(\PageIndex{1}\) shows a visualization for an observer flying through a cube at \(v = 0.99\). In figure \(\PageIndex{1}\) (1), the cube is shown in its own rest frame, where it has sides of unit length, and the observer, having already passed through, lies one unit to the right of the cube’scenter. The observer is facing to the right, away from the cube. The dashed line is a ray of light that travels from point \(P\) to the observer, and in this frame it appears as though the ray, arriving from \(\theta = 162^{\circ}\), would not make it into the observer’s eye.
But in the observer’s frame, figure \(\PageIndex{1}\) (2), the ray is at \(\theta ' = 47^{\circ}\), so it actually does fall within her field of view. The cube is length-contracted by a factor \(γ ≈ 7\). The ray was emitted earlier, when the cube was out in front of the observer, at the position shown by the dashed outline.
The image seen by the observer is shown in figure \(\PageIndex{1}\) (3). The circular outline defining the field of view represents \(\theta ' = 50^{\circ}\). Note that the relativistic length contraction is not at all what an observer sees optically. The optical observation is influenced by length contraction, but also by aberration and by the time it takes for light to propagate to the observer. The time of propagation is different for different parts of the cube, so in the observer’s frame, figure \(\PageIndex{1}\) (2), rays from different points had to be emitted when the cube was at different points in its motion, if those rays were to reach the eye.
A group at Australian National University has produced animations of similar scenes, which can be found online by searching for “optical effects of special relativity.”
The video shows photorealistic representations of reduced c scenes. This means that the speed of light has been slowed down from over one billion kilometres per hour to a speed of only one meter per second. The consequences of this fiction have been restricted to optical effects, and allows us to see special-relativistic effects not possible in everyday life.
It’s fun to imagine the view of an observer on board an ultrarelativistic starship. For \(v\) sufficiently close to \(1\), any angle \(\theta < 180^{\circ}\) transforms to a small \(θ'\). Thus, all light coming to this observer from the surrounding stars — even those in extreme backward directions! — is gathered into a small, bright patch of light that appears to come from straight ahead. Some visible light would be shifted into the extreme ultraviolet and infrared, while some infrared and ultraviolet light would become visible.


