9.5: Congruences, Expansion, and Rigidity
- Page ID
- 3477
Learning Objectives
- Explain mathematical techniques to approach the different issues such as expansion, rotation and shear
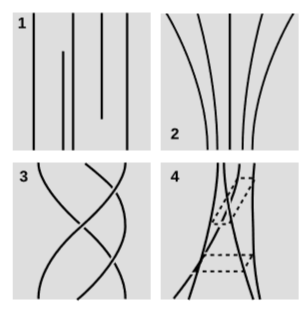
This chapter has focused on fluxes of conserved quantities; we wanted to rule out pictures like figure \(\PageIndex{1}\) (1), in which the appearance and disappearance of world-lines would imply nonconservation of properties such as charge and mass-energy. But the mathematical techniques we’ve developed turn out to be an elegant way to approach the different issues described in the other parts of figure \(\PageIndex{1}\).
Congruences
In figure \(\PageIndex{1}\) (2), we have expansion. For example, the world-lines could represent galaxies getting farther apart because of cosmological expansion resulting from the Big Bang. We do not expect rulers to expand or contract, in the sense that although a ruler may exhibit Lorentz contraction, it should always have the same length in its own rest frame unless it has been mechanically stressed or altered.
If there is more than one spatial dimension, then we can have rotation, as in figure \(\PageIndex{1}\) (3). These world-lines could represent a constellation of orbiting satellites, or fixed points in a rotating laboratory.
The other interesting possibility, if there is more than one spatial dimension, is shear, figure \(\PageIndex{1}\) (4). Here the rectangular group of four particles contracts in one direction while expanding in the other so as to keep the enclosed \(2\)-volume constant.
In order to discuss these possibilities, it is convenient to define the notion of a timelike congruence, which is a set of nonintersecting, smooth, timelike world-lines whose union constitutes all the events in some region of spacetime. That is, we “fill in” spacetime with an infinite number of world-lines so that there is no space between them. This is something like the grain in a piece of wood, or Faraday’s conception of field lines filling space, except that one of our \(n + 1\) dimensions is timelike, and the lines aren’t allowed to point in directions that lie outside the light cone. One way to specify a congruence is to give the normalized velocity vector that is tangent to the world-line passing through any given point.
Example \(\PageIndex{1}\): An expanding congruence
As an example of a congruence in \(1+1\) dimensions, consider the set of all curves of the form \(x = ae^{bt}\), where \(a\) and \(b\) are positive constants. It would look like figure \(\PageIndex{1}\) (2). Let
\[u = \frac{\mathrm{d} x}{\mathrm{d} t} = abe^{bt}\]
the velocity vector is
\[v^λ = γ^{-1} (1,u)\]
where the factor of \(\gamma ^{-1} = \sqrt{1 - u^2}\) gives the proper normalization \(v^λ v_λ = 1\).
Example \(\PageIndex{2}\): A boring congruence
Suppose we instead let the congruence consist of the set of all curves of the form \(x = c + ut\), where \(c\) and \(u\) are constants and \(|u| < 1\). Then as in the above example, \(v^λ = γ^{-1} (1,u)\). The world-lines are inertial and parallel to one another.
Expansion and rigidity
For the remainder of this discussion, we restrict ourselves to the \(1 + 1\)-dimensional case, so that rotation and shear are impossible, and the only interesting question is whether a given congruence has expansion. In \(1 + 1\) dimensions, the congruence can be specified by giving the function \(u(x,t)\), where as in examples above, \(u = dx/dt\). If \(u\) is constant, then we have example \(\PageIndex{2}\), and clearly there is no expansion. Thus expansion requires either \(∂u/∂t\) or \(∂u/∂x\), or both, to be nonzero.
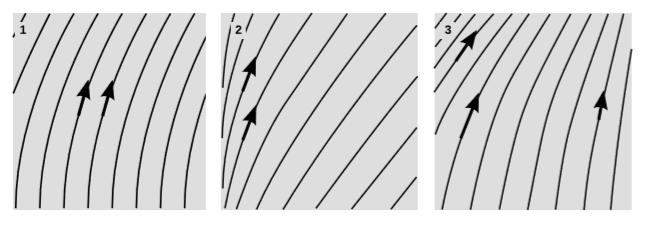
Figure \(\PageIndex{1}\) (1) shows the case where \(∂u/∂x = 0\) and \(∂u/∂t \neq 0\). Each world-line is a copy of the others that has been shifted spatially, and the two velocity vectors shown as arrows are equal. This is precisely Bell’s spaceship paradox (section 3.9). Although the horizontal spacing between the world-lines remains constant as defined by the fixed frame of reference used for the diagram, an observer accelerating along with one of the particles would find that they had expanded away from one another, because the observer’s meter-sticks have Lorentz-contracted. This is a real expansion in the sense that if the world-lines are particles in a solid object, the object comes under increasing tension.
In figure \(\PageIndex{2}\) (2) we have \(∂u/∂t = 0\) and \(∂u/∂x \neq 0\). The world-lines are copies of one another that have been shifted temporally. The two velocity vectors in the diagram are the same. All of the particles began accelerating from the same point in space, but at different times. Here there is clearly an expansion, because the world-lines are getting farther apart.
Suppose that we accelerate a rigid object such as a ruler. Then we must have something like figure \(\PageIndex{2}\) (3). To avoid the situations described in \(\PageIndex{2}\) (1) and \(\PageIndex{2}\) (2), the velocity vector must vary with both \(t\) and \(x\); the three velocity vectors in the figure are all different. As the particles accelerate, the spacing between them Lorentz-contracts, so that an observer accelerating along with them sees the spacing as remaining constant.
This notion of rigid motion in relativity is called Born rigidity. No physical substance can naturally be perfectly rigid (Born rigid), for if it were, then the speed at which sound waves traveled in it would be greater than c. Born rigidity can only be accomplished through a set of external forces applied at all points on the object according to a program that has been planned in advance. A real object such as a ruler does not maintain its own Born-rigidity, but it will eventually return to its original size and shape after having undergone relativistic acceleration, due to its own elastic properties, provided that the acceleration has been gentle enough to avoid permanently damaging it. In \(1+1\) dimensions, Born rigidity is equivalent to a lack of expansion. In \(3 + 1\) dimensions, we also require vanishing shear.
Mathematically, it is clear that the condition of vanishing expansion must be expressible in \(1 + 1\) dimensions in terms of the partial derivatives \(∂u/∂t\) and \(∂u/∂x\), and since we have been able to describe the condition in a frame-independent way (by referring it to observations made by the comoving observer), it should also be something we can express as a scalar within the grammar of index gymnastics. There is only one possible way to express such a condition, which is
\[∂_a v^a = 0\]
We can in fact define a scalar \(Θ\), called the expansion scalar, according to
\[Θ = ∂_a v^a\]
This definition is valid in \(n+1\) dimensions, but in \(1+1\) dimensions it reduces to
\[\Theta = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\]
The expansion scalar is interpreted as the fractional rate of change in the volume of a set of particles that move along the worldlines defined by the congruence, where the rate of change is defined with respect to the proper time \(τ\) of an observer moving along with the particles. For example, cosmological expansion leads to a fractional increase in the distances between galaxies \(∆L/L\) which, for a small time interval \(∆τ\), is equal to \(H_o∆τ\), where \(H_o\), called the Hubble constant, is about \(2.3×10^{-18}\; s^{-1}\). That is, the fractional rate of change is \((1/L)dL/dτ = H_o\). Because distances expand in all three spatial dimensions, the fractional rate of change of volume is
\[\Theta = \frac{1}{V}\frac{\mathrm{d} V}{\mathrm{d} \tau } = 3H_o\]
In this example, spacetime is not flat, so we would have to express \(Θ\) in terms of the covariant derivative \(∇_a\) defined in section 9.4, not the partial derivative \(∂a\).
Example \(\PageIndex{3}\): A catastrophe
Consider the timelike congruence in \(1+1\) dimensions defined by \(u = x/t\). This consists of the set of all inertial world-lines passing through the origin. Since our definition of a congruence requires that the world-lines be non-intersecting, let’s restrict this example to the interior of the past light cone of the origin, \(|x| < -t\). We have a universe full of hapless particles, all heading like lemmings toward a catastrophic collision. The spacetime diagram looks like an optical ray diagram for the formation of a real image. A computation gives the unexpectedly simple result \(Θ = γ/t\). For \(t < 0\), this is negative, indicating a contraction, and it blows up to minus infinity as \(t\) approaches \(0\).
Caustics
The apex of the cone in example \(\PageIndex{3}\) is a caustic. Given a spacefilling set of straight lines, a caustic occurs where their intensity diverges to infinity. The word means “burning,” because in optics a caustic of light rays concentrates energy and can burn things. Example \(\PageIndex{3}\) involves a caustic of timelike world-lines, and “straight” is to be interpreted as meaning that the world-lines are inertial.
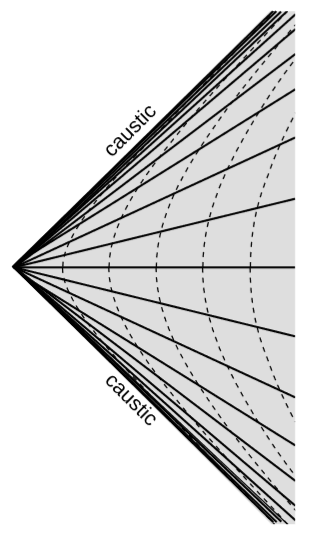
Figure \(\PageIndex{4}\) shows two caustics formed by spacelike lines for the accelerated coordinate system described in section 7.1. Here, as is often the case, the caustics are not just points.
An example from general relativity is that when a black hole forms by gravitational collapse, a caustic is formed at a one point by the set of lightlike world-lines that enter the event horizon from the outside universe at the moment when the horizon is formed. If a ray of light is emitted from this caustic point, it remains on the event horizon forever, as do all rays emitted at the horizon in the outward direction at later times. The event horizon is the same set of events as the union of all the lightlike world-lines that enter the horizon at the caustic.4
The Herglotz-Noether theorem in 1+1 dimensions
Certain Born-rigid types of motion are possible, and others are not, purely as a matter of kinematics. It turns out to be possible to accelerate a rod in a Born-rigid way along its own length, but surprisingly, it is not possible, for example, for a sphere to remain Born-rigid while simultaneously rotating and having its center of mass accelerated. The possible types of motion are delineated by a theorem called the Herglotz-Noether theorem. Unlike the \(3+1\)-dimensional version of the theorem, the \(1+1\)-dimensional version is neither surprising nor difficult to state or prove.
Herglotz-Noether theorem in \(1+1\) dimensions: Any rigid motion in \(1 + 1\) dimensions is uniquely determined by the world-line \(W\) of one point, provided that the world-line of that point is smooth and timelike. It is in general only possible to extend the congruence describing the motion to some neighborhood of \(W\).
Proof
To avoid technical issues, we assume that “smooth” means analytic, which slightly weakens the result. As discussed above, zero expansion is equivalent to \(0 = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\), where \((t,x)\) are any set of Minkowski coordinates. This can be put in the form \(\frac{\partial u}{\partial x} = f(u) \frac{\partial u}{\partial t}\), where \(f\) is smooth for \(-1 < u < 1\) and \(f(0) = 0\). We need to prove that the solution of this partial differential equation, if it exists, is unique given \(W\). We arbitrarily choose one event on \(W\). By assumption, \(W\) is timelike at this point, so we are free to choose our Minkowski coordinates such that our point is at rest at this event at the origin. Since \(f(0) = 0\), it follows that at the origin \(∂u/∂x = 0\). We can similarly evaluate the higher derivatives \(∂^n u/∂x^n\), and because \(u\) is smooth we can in this calculation freely interchange the order of the partial derivatives \(∂x\) and \(∂t\). It is straightforward to show that these higher derivatives \(∂^n u/∂x^n\) are also zero. Since \(u(x)\) is assumed to be analytic, it follows that \(u(0,x) = 0\) for all \(x\), i.e., an observer instantaneously moving along \(W\) at \(t = 0\) says that all other points are at rest as well at that time. But because \(W\) is timelike, we can always find some neighborhood \(A\) of \(W\) such that every point in \(A\) is simultaneous with a unique event on \(W\) according to an observer at that event moving along with \(W\). Therefore the value of \(u\) is determined everywhere in \(A\), and this completes the proof that the congruence exists and is unique in \(A\).
Remarks
- The \(1 + 1\)-dimensional version of the Herglotz-Noether theorem is not a special case of the \(3 + 1\)-dimensional version. The latter is usually proved for a space-filling congruence, and it fails when the body in question does not enclose a volume, e.g., in the case of a thin rod or a letter “C.”
- The theorem can be strengthened by relaxing the requirement of smoothness so that only the existence of a second derivative of the position with respect to proper time is required. 5
- If the motion is accelerated, then the rigid motion cannot be extended to an arbitrary distance from \(W\). If the proper acceleration of \(W\) can be as great as a, then as in example ??, p. ??, we expect to be able to extend the rigid motion to a proper distance only as big as \(c^2/a\), where there will be a caustic similar to the one in figure \(\PageIndex{4}\).
Bell’s spaceship paradox revisited
Bell’s spaceship paradox was discussed in section 3.9. In the paradox, two spaceships begin accelerating simultaneously and have equal accelerations in the frame of an external, inertial observer, causing a thread stretched between them breaks. We now give a more rigorous and mathematically elegant demonstration of the same result, suggested by P. Allen.
The motion of the thread throughout its length can be described by a timelike congruence. If the thread is not to come under any strain, then this must be a Born-rigid congruence. By the \(1+1\)-dimensional Herglotz-Noether theorem, the congruence is uniquely determined by the motion of one of its points, which we take to be the trailing rocket. This congruence happens to be known. It is defined by the system of accelerated coordinates (Rindler coordinates) described in section 7.1. The vanishing of the expansion scalar for this congruence is left for the reader to verify. But this congruence consists of world-lines whose proper accelerations are each constant and all different from one another, and this is inconsistent with the description given in the Bell paradox, where it is stated that a frame exists in which the motions of the two ships are identical except for a translation. Therefore the thread cannot move rigidly.
This completes the resolution fo the paradox, but as an illustrative example, we present an explicit calculation of the expansion scalar for the congruence that one would most naturally imagine to be implied by the description of the paradox. This is given by \((x + c)^2 = 1 + t^2\). For a given value of the parameter \(c\), we get an accelerating world-line. (Its proper acceleration \(a = 1\) happens to be constant, although this is not necessary for the purposes of discussing the paradox.) Each world-line starts at rest at \(t = 0\), and each one has the same acceleration at any given \(t\). By picking any two distinct values of \(c\) as the endpoints of the thread, we obtain the literal situation described in the paradox.
Implicit differentiation gives \(u = \frac{t}{\sqrt{1 + t^2}}\). The algebra gets a little messy now, so I used the open-source computer algebra system Maxima. The following program, which should be fairly readable without previous knowledge of Maxima’s syntax, calculates the expansion tensor:
- u:t/sqrt(1+t^2);
- gamma:1/sqrt(1-u^2);
- theta:diff(gamma,t)+diff(u*gamma,x);
- is(equal(theta,gamma*u^2/t));
The third line prints out a complicated expression for \(Θ\), which the fourth line shows can be simplified to \(γu^2/t\). This is positive for \(t > 0\), which shows that the thread is forced to expand. Note that although the calculation was carried out in a particular set of coordinates, a relativistic scalar such as \(Θ\) has a coordinate-independent value. Reference to a particular coordinate system or frame of reference occurs only in the initial definition of the congruence, which is defined in order to model the situation described in the paradox, which is stated in terms of a particular external observer.


