Hip Forces
- Page ID
- 3360
Forces on the Leg
In this little document we look at the forces acting on the leg, with particular attention to the forces at the top of the femur. We first consider a person standing on one leg, and then look at the use of a cane when there is a hip injury.
A Person Standing on One Leg
A person is standing stationary on one leg. We shall analyze the forces acting on the leg. The figure shows the force diagram.

The person has a weight of W.
The normal force N of the floor on the foot has a magnitude equal to W and acts under the center of gravity of the whole body of the person.
The abductor muscles are attached to the outside greater trochanter of the femur, and experimentally Inman found that the force F exerted on the trochanter acts at an angle of 70 degrees to the horizontal.
The weight of the leg WL is typically about 1/7 of the weight of the person, and, as shown in the diagram, that force acts at the center of gravity of the leg. The center of gravity of the leg is about 5/9 of the distance from the greater trochanter to the foot.
R is the force exerted by the socket of the pelvis, the acetabulum, on the head of femur.
The figure indicates the horizontal positions of where the forces act relative to the position where R is applied.
Analysis
Since the person is stationary, the horizontal and vertical components of the forces and the total torque are all equal to zero.
\[\sum F_H=~0\tag{1}\]
\[\sum F_V=~0\tag{2}\]
\[\sum \tau=~0 \tag{3}\]
The horizontal components of the forces are:
\[\sum F_H=F\cos(70)-R_H\tag{4}\]
The vertical components of the forces are:
\[\sum F_V=F\sin(70)-R_V-\frac{W}{7}+W\tag{5}\]
We can analyze the torques about any pivot point. We shall choose the point where the force R is exerted on the femur by the pelvis. As usual, we also have positive torques tending to cause counter-clockwise rotations, and negative torques tending to cause clockwise rotations. Then the total torque is:
\[\sum \tau=F\sin(70)7+\left[\frac{W}{7}\right]3-W11 \tag{6}\]
The above equations are in terms of the vertical and horizontal components of the force R, RH and RV. These are related to the magnitude of R by:
\[R=\sqrt{R_H^2+R_V^2}\tag{7}\]
The solution to all of these equations is:
F = 1.6 W
R = 2.4 W
The angle ![]() is calculated from: tan(
is calculated from: tan(![]() ) = RH/RV and is found to be:
) = RH/RV and is found to be:
\[\varphi =0.23 ~radians=13^\circ\]
Conclusions
The first conclusions from the above analysis are that the force exerted on the head of the femur by the pelvis, R, is very large, 2.4 times the weight of the person, and that the force F exerted on the trochanter by the abductor muscles is also large, 1.6 W. These two forces are directed in nearly opposite directions and 7 cm away from each other. Thus the upper femur experiences large forces of compression and shear.
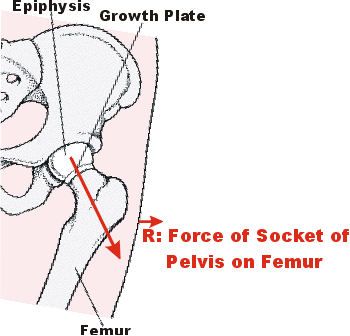 The figure to the right shows the anatomy of the upper part of the femur and pelvis.
The figure to the right shows the anatomy of the upper part of the femur and pelvis.
The epiphysis is not strongly attached to the rest of the bone, and can slip out of place. This slipped capital femoral epiphysis is particularly common during the adolescent growth spurt.
The direction of the force R exerted on the epiphysis, which we have just calculated to be 13 degrees from the vertical, is such that the epiphysis has very little sideways force exerted on it.
Thus, our second conclusion is that this bio-mechanical system is well designed to try to minimize slippage of the epiphysis.
Extending the Model to a Person Walking
If you spend a few minutes observing yourself and others walking, you may come to the conclusion that the force diagram for a person standing motionless on one leg is similar to a walking person except that:
- When walking we are not in equilibrium. If we stop in mid-stride we have a tendency to fall over.
- In mid-stride the leg is approximately vertical so the vertical point of application of the forces N, W/7 and R are approximately lined up.
- If we stop in mid-stride, to avoid falling over we must shift our body weight by just a couple of centimeters to correspond to our previous analysis.
Thus, when walking most people will experience forces on the trochanter and epiphysis of roughly the same magnitude and direction as our analysis of a person standing motionless on one leg.
Using a Cane When a Hip Is Injured
Typically a person can support about one-sixth of their weight with a cane. Suppose a person has injured their hip and is using a cane. The question is should they use the cane on the same side as the injured hip or on the opposite side.
Using a Cane On the Same Side As the Injury
 If you obtain a cane and walk while placing the cane on the same side as an imagined sore hip, you will observe that:
If you obtain a cane and walk while placing the cane on the same side as an imagined sore hip, you will observe that:
- You place the cane right next to your foot.
- If you stop in mid-stride you have very little tendency to fall over: you are almost in equilibrium.
Thus the force diagram and analysis for a person standing motionless on one leg is very close to this case. There is one difference:
The normal force N exerted on the foot by the floor is reduced from the weight W of the person to 5/6 W. The other sixth of the person's weight is being supported by the cane.
The result of doing the math is that:
F = 1.3 W
R = 2.0 W
These are both less than without using the cane.
Using a Cane on the Opposite Side to the Injury
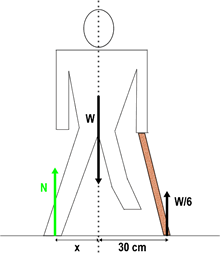 If you imagine a sore hip and walk while placing the cane on the opposite side to the injury, you will observe that:
If you imagine a sore hip and walk while placing the cane on the opposite side to the injury, you will observe that:
- You place the cane fairly far from the center line of your body: 30 cm is a typical figure.
- Just as in using the cane on the same side as the injury, in mid-stride you are again very close to equilibrium.
Thus, the total vertical force at mid-stride is approximately zero:
W - W/6 - N = 0
The total torque is also zero. Evaluating about the midline, we write:
N x = W/6 * 30 cm
Thus:
N = 5 W / 6
x = 6 cm
Now we can do an analysis similar to the one for the person standing motionless on one leg. In addition to the reduced value of the normal force N exerted on the foot by the floor, the only other differences are that:
- The center of mass of the leg has shifted.
- The point of application of the normal force N of the floor on the foot has shifted.
Doing the math we end up with the results:
F = 0.6 W
R = 1.3 W
Conclusions
The results of this analysis are probably counter-intuitive: when a hip is injured a cane should be used on the opposite side to the injury. The table summarizes:
| Force of Abductor Muscle | Force on Epiphysis | |
|---|---|---|
| No Cane | ~ 1.6 W | ~ 2.4 W |
| Cane Same Side | 1.3 W | 2.0 W |
| Cane Opposite Side | 0.6 W | 1.3 W |
Reference
Some of the above analysis appears in R.K. Hobbie, Intermediate Physics for Medicine and Biology (Wiley, 1978, ISBN 0-471-03212-3), pgs 8-13.

