4.1: Error Function
- Page ID
- 7228
Before we start this chapter, let’s just make sure that we are familiar with the error function erf a. We may need it during this chapter.
Here is a graph of the gaussian function
\[ y = \frac{1}{ \sqrt{ \pi}} e^{-x^2}.\]
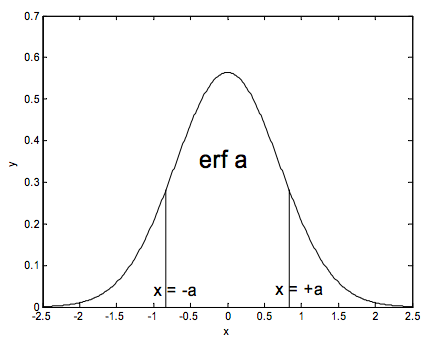
I have chosen the coefficient \(1/ \sqrt{\pi}\) so that the area under the curve, from − ∞ to + ∞ is 1. The maximum value, which occurs at x = 0, is \(1/ \sqrt{ \pi} = 0.5642\), and it is easy to show that the half width at half the maximum is \( \sqrt{ \ln 2} = 0.8326\). Also of some interest (though not particularly in this chapter) is the square root of the second moment of area around the y-axis. In a mechanical context this would be called the radius of gyration. In a statistical context it would be called the standard deviation. Either way, its value is \(1/ \sqrt{2} = 0.7071\). We shall meet the gaussian function again in Chapter 6.
In the present chapter we shall need to make use of the error function erf a. This is the area under the gaussian curve from x = -a to x = +a:
\[ \text{erf} a = \frac{1}{ \sqrt{ \pi}} \int_{- a}^{+ a} e^{-x^2} dx.\]
The area outside the limits x = ±a, which is the area under the two “tails” of the gaussian function, is sometimes called the complementary error function:
\[ \text{erfc} a = 1 - \text{erf} a\]
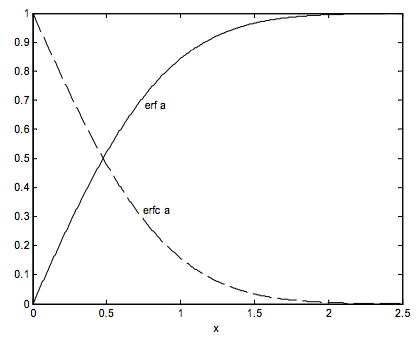
It will be clear that erf a goes from 0 to 1 as a goes from 0 to infinity. Note also that
erfc (one standard deviation) = 0.3173
erfc (two standard deviations) = 0.0455.
Here are graphs of erf a (continuous line) and erfc a (dashed line) versus a.