1.3: Fluid Statics

Last updated
Save as PDF

Page ID: 6331

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

I mentioned above that statistical mechanics asks questions like “How does the pressure change with volume?”. But what is pressure? Most people will answer by saying that pressure is force per area:

\[\text { pressure }=\frac{\text { force }}{\text { area }}.\]

But force is a vector and pressure is a scalar, so how can this formula be correct? The aim of this section is to investigate what this formula means and find out when it is correct.²

1.3.1 Problems

1.1 (I) The rotating water glass

A cylinder containing a fluid of mass density ρ is placed on the center of a phonograph turntable and rotated with constant angular velocity ω. After some initial sloshing of the fluid, everything calms down to a steady state.

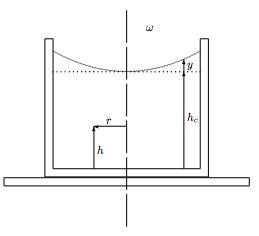
Screen Shot 2019-07-19 at 1.31.25 PM.png

a. The pressure is a function of height h and distance from the axis r. Show that the variation of pressure with radial distance is

\[\frac{\partial p(r, h)}{\partial r}=\rho \omega^{2} r,\]

while the variation with vertical distance is

\[\frac{\partial p(r, h)}{\partial h}=-\rho g.\]

(Where g is the acceleration of gravity.)

b. The pressure at the surface of the fluid at the center of the cylinder (r = 0, h = h_c) is of course atmospheric pressure pa. Integrate the differential equations of part (a.) to show that, at any point in the fluid,

\[p(r, h)=p_{a}+\frac{1}{2} \rho \omega^{2} r^{2}-\rho g\left(h-h_{c}\right).\]

c. Show that the profile of the fluid surface is given by

\[y(r)=\frac{\omega^{2}}{2 g} r^{2}.\]

²As such, the aim of this section is quite modest. If you want to learn more about the interesting subject of fluid flow, see the “Resources” section of this chapter.