8.4: Distribution Functions

8.4.1 One-particle distribution functions

What is the mean number of particles in the box of volume d³r_A about r_A?

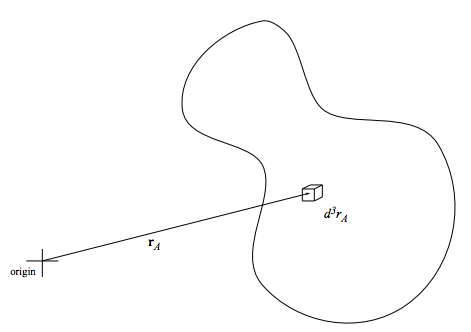
The probability that particle 1 is in d³r_A about r_A is

\[ \frac{d^{3} r_{A} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{A}, \mathbf{r}_{2}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}.\]

The probability that particle 2 is in d³r_A about r_A is

\[ \frac{\int d^{3} r_{1} \quad d^{3} r_{A} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{A}, r_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, r_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}.\]

And so forth. I could write down N different integrals, but all of them would be equal.

Thus the mean number of particles in d³r_A about r_A is

\( \pi_{1}\left(\mathbf{r}_{A}\right) d^{3} \boldsymbol{T}_{A}\)

\[ =N \frac{d^{3} r_{A} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{A}, \mathbf{r}_{2}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}\]

\[ =N \frac{d^{3} r_{A} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{A}, r_{2}, r_{3}, \ldots, r_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{h^{3 N} N ! Z(T, V, N)}\]

\[ =\frac{1}{(N-1) !} \frac{d^{3} r_{A} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} e^{-\beta U\left(r_{A}, r_{2}, r_{3}, \ldots, r_{N}\right)}}{Q(T, V, N)}\]

8.4.2 Two-particle distribution functions

What is the mean number of pairs of particles, such that one member of the pair in a box of volume d³r_A about r_A and the other member is in a box of volume d³r_B about r_B?

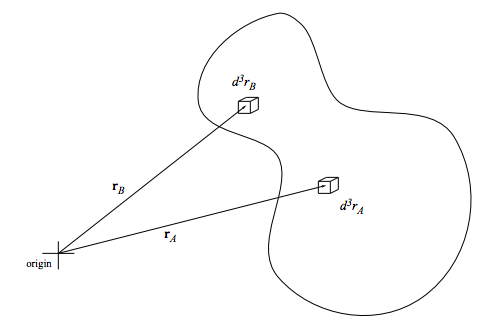
The probability that particle 1 is in d³r_A about r_A and particle 2 is in d³r_B about r_B is

\[ \frac{d^{3} r_{A}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{A}, \mathbf{r}_{B}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}.\]

The probability that particle 2 is in d³r_A about r_A and particle 1 is in d³r_B about r_B is

\[ \frac{d^{3} r_{B} d^{3} r_{A} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{B}, r_{A}, r_{3}, \ldots, r_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, r_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}.\]

The probability that particle 3 is in ³r_A about r_A and particle 1 is in d³r_B about r_B is

\[ \frac{d^{3} r_{B} \int d^{3} r_{2} d^{3} r_{A} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{B}, \mathbf{r}_{2}, r_{A}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, r_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}.\]

And so forth. I could write down N(N − 1) different integrals, but all of them would be equal.

Thus the mean number of pairs with one particle in d³r_A about r_A and the other in d³r_B about r_B is

\( n_{2}\left(\mathbf{r}_{A}, \mathbf{r}_{B}\right) d^{3} r_{A} d^{3} r_{B}\)

\[ =N(N-1) \frac{d^{3} r_{A} d^{3} r_{B} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{A}, \mathbf{r}_{B}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}{\int d^{3} r_{1} \int d^{3} r_{2} \int d^{3} r_{3} \cdots \int d^{3} r_{N} \int d^{3} p_{1} \cdots \int d^{3} p_{N} e^{-\beta H\left(\mathbf{r}_{1}, \mathbf{r}_{2}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}, \mathbf{p}_{1}, \ldots, \mathbf{p}_{N}\right)}}\]

\[ =\frac{1}{(N-2) !} \frac{d^{3} r_{A} d^{3} r_{B} \int d^{3} r_{3} \cdots \int d^{3} r_{N} e^{-\beta U\left(\mathbf{r}_{A}, \mathbf{r}_{B}, \mathbf{r}_{3}, \ldots, \mathbf{r}_{N}\right)}}{Q(T, V, N)}.\]

Problems

8.7 Correlations of nearby particles

Suppose that (as is usual) at small distances the interatomic potential u(r) is highly repulsive. Argue that at small r,

\[ g_{2}(r) \approx \text { constant } e^{-u(r) / k_{B} T}.\]

Do not write down a long or elaborate derivation. . . I’m looking for a simple qualitative argument.

8.8 Correlations between non-interacting identical quantal particles

Guess the form of the pair correlation function g₂(r) for ideal (non-interacting) fermions and bosons. Sketch your conjectures, and then compare them to the graphs presented by G. Baym in Lectures on Quantum Mechanics (W.A. Benjamin, Inc., Reading, Mass., 1969) pages 428 and 431.

8.9 Correlation functions and structure factors

A typical isotropic fluid, at temperatures above the critical temperature, has correlation functions that are complicated at short distances, but that fall off exponentially at long distances. In fact, the long-distance behavior is

\[ g_{2}(r)=1+\frac{A e^{-r / \xi}}{r}\]

where ξ, the so-called correlation length, depends on temperature and density. In contrast, at the critical temperature the correlation function falls off much more slowly, as

\[ g_{2}(r)=1+\frac{A}{r^{1+\eta}}\]

Find the structure factor

\[ S(\mathbf{k})=\int d^{3} r\left[g_{2}(\mathbf{r})-1\right] e^{-i \mathbf{k} \cdot \mathbf{r}}\]

associated with each of these correlation functions. Will your results match those of experiments at small values of k or at large values (i.e. at long or short wavelengths)?

8.10 Long wavelength structure factor

Show that, for an isotropic fluid, \( \frac{d S(k)}{d k}\) vanishes at k = 0. Here S(k) is the structure factor

\[ S(\mathbf{k})=1+\rho \int d^{3} r\left[g_{2}(\mathbf{r})-1\right] e^{i \mathbf{k} \cdot \mathbf{r}}.\]

8.11 Correlations in a magnetic system

In the Ising model for a magnet, described in problem 4.9, the (net) correlation function is defined by

\[ G_{i} \equiv\left\langle s_{0} s_{i}\right\rangle-\left\langle s_{0}\right\rangle^{2},\]

where the site j = 0 is some arbitrary “central spin”. Using the results of problem 4.9, show that for a lattice of N sites,

\[ \chi_{T}(T, H)=N \frac{m^{2}}{k_{B} T} \sum_{i} G_{i}.\]