B15: Magnetic Field Introduction - Effects
( \newcommand{\kernel}{\mathrm{null}\,}\)
We now begin our study of magnetism, and, analogous to the way in which we began our study of electricity, we start by discussing the effect of a given magnetic field without first explaining how such a magnetic field might be caused to exist. We delve into the causes of magnetic fields in subsequent chapters.
A magnetic field is a vector field. That is, it is an infinite set of vectors, one at each point in the region of space where the magnetic field exists. We use the expression “magnetic field” to designate both the infinite set of vectors, and, when one is talking about the magnetic field at a point in space, the one magnetic field vector at that point in space. We use the symbol \vec{B} to represent the magnetic field. The most basic effect of a magnetic field is to exert a torque on an object that has a property known as magnetic dipole moment, and, that finds itself in the magnetic field. A particle or object that has a non-zero value of magnetic dipole moment is called a magnetic dipole. A magnetic dipole is a bar magnet. The value of the magnitude of the magnetic dipole moment of an object is a measure of how strong a bar magnet it is. A magnetic dipole has two ends, known as poles—a north pole and a south pole. Magnetic dipole moment is a property of matter which has direction. We can define the direction, of the magnetic dipole moment of an object, by considering the object to be an arrow whose north pole is the arrowhead and whose south pole is the tail. The direction in which the arrow is pointing is the direction of the magnetic dipole moment of the object. The unit of magnetic dipole moment is the A\cdot m^2 (ampere meter-squared). While magnetic compass needles come in a variety of magnetic dipole moments, a representative value for the magnetic dipole moment of a compass needle is .1A\cdot m^2.
Again, the most basic effect of a magnetic field is to exert a torque on a magnetic dipole that finds itself in the magnetic field. The magnetic field vector, at a given point in space, is the maximum possible torque-per-magnetic-dipole-moment-of-would-be-victim that the magnetic field would/will exert on any magnetic dipole (victim) that might find itself at the point in question. I have to say “maximum possible” because the torque exerted on the magnetic dipole depends not only on the magnitude of the magnetic field at the point in space and the magnitude of the magnetic dipole moment of the victim, but it also depends on the orientation of the magnetic dipole relative to the direction of the magnetic field vector. In fact:
\vec{\tau}=\vec{\mu}\times \vec{B}\label{15-1}
where \vec{\tau} is the torque exerted on the magnetic dipole (the bar magnet) by the magnetic field, \vec{\mu} is the magnetic dipole moment of the magnetic dipole (the bar magnet, the victim), and \vec{B} is the magnetic field vector at the location in space at which the magnetic dipole is.
For the cross product of any two vectors, the magnitude of the cross product is the product of the magnitudes of the two vectors, times the sine of the angle the two vectors form when placed tail to tail. In the case of \vec{\tau}=\vec{\mu}\times \vec{B}, this means:
\tau=\mu\space B\sin\theta \nonumber
In the SI system of units, torque has units of N\cdot m (newton-meters). For the units on the right side of \tau=\mu\space B\cos \theta to work out to be N\cdot m, what with \muhaving units of electric dipole moment (A\cdot m^2 ) and \sin \theta having no units at all, B must have units of torque-per-magnetic-dipole-moment, namely, \frac{N\cdot m}{A\cdot m^2}. That combination unit is given a name. It is called the tesla, abbreviated T.
1T= 1\frac{N\cdot m}{A\cdot m^2} \nonumber
Example 1
Consider a magnetic dipole having a magnetic dipole moment \mu=0.045 \, A\cdot m^2, oriented so that it makes an angle of 23^{\circ} with the direction of a uniform magnetic field of magnitude 5.0\times10^{-5} T as depicted below. Find the torque exerted on the magnetic dipole, by the magnetic field.
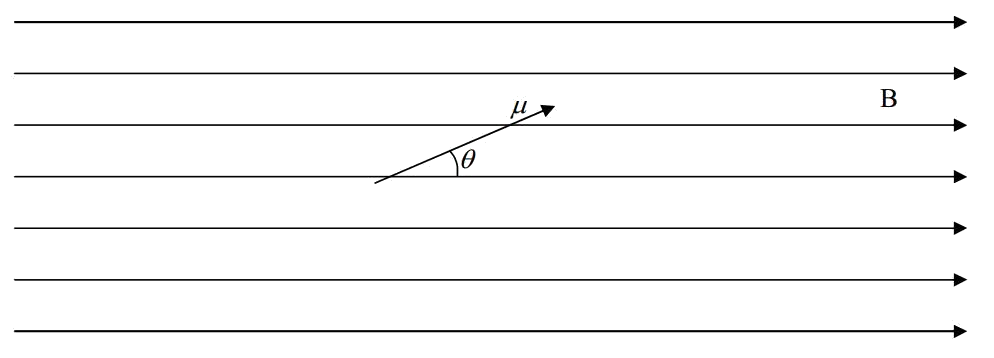
Recall that the arrowhead represents the north pole of the bar magnet that a magnetic dipole is. The direction of the torque is such that it tends to cause the magnetic dipole to point in the direction of the magnetic field. For the case depicted above, that would be clockwise as viewed from the vantage point of the creator of the diagram. The magnitude of the torque for such a case can be calculated as follows:
\begin{align*} \tau &=\mu B\sin\theta \\[4pt] &=(.045A\cdot m^2)(5.0\times10^{-5}T)\sin 23^{\circ} \\[4pt] &=8.8\times 10^{-7} A\cdot m^2 \cdot T \end{align*}
Recalling that a tesla is a \frac{N\cdot m}{A\cdot m^2} we have:
\begin{align*} \tau&=8.8\times 10^{-7} A\cdot m^2 \cdot \frac{N\cdot m}{A\cdot m^2} \\[4pt] &=8.8\times 10^{-7} N\cdot m \end{align*}
Thus, the torque on the magnetic dipole is \tau=8.8\times 10^{-7} N\cdot m clockwise, as viewed from the vantage point of the creator of the diagram.
Example 2
A particle having a magnetic dipole moment \vec{\mu}=0.025 A\cdot m^2 \hat{i}-0.035 A\cdot m^2 \hat{j}+0.015 A\cdot m^2 \hat{k} is at a point in space where the magnetic field \vec{B}=2.3 mT \hat{i}+5.3mT\hat{j}-3.6mT\hat{k}. Find the torque exerted on the particle by the magnetic field.
Solution
\begin{align*} \vec{\tau} &=\vec{\mu}\times \vec{B} \\[4pt] &=\begin{vmatrix} \hat{i}&\hat{j}&\hat{k}\\ 0.025A\cdot m^2&-0.035 A\cdot m^2&0.015 A\cdot m^2 \\ 0.0023 \frac{Nm}{Am^2} &0.0053 \frac{Nm}{Am^2} & -0.0036 \frac{Nm}{Am^2}\end{vmatrix} \\[4pt] &=\hat{i} \Big[(-0.035Am^2)(-0.0036 \frac{Nm}{Am^2})-(0.015Am^2)(0.0053 \frac{Nm}{Am^2}) \Big]\\[4pt] &+\hat{j} \Big[ (0.015Am^2)(0.0023 \frac{Nm}{Am^2})-(0.025Am^2)(-0.0036 \frac{Nm}{Am^2}) \Big] \\[4pt] &+\hat{k} \Big[ (0.025Am^2)(0.0053 \frac{Nm}{Am^2})-(-0.035Am^2)(0.0023 \frac{Nm}{Am^2}) \Big] \\[4pt] &=1.2\times10^{-4} Nm \hat{i}-1.2\times 10^{-4} Nm \hat{j}+2.1\times 10^{-4} Nm\hat{k} \end{align*}
The Magnetic Force Exerted Upon a Magnetic Dipole
A uniform magnetic field exerts no force on a bar magnet that is in the magnetic field. You should probably pause here for a moment and let that sink in. A uniform magnetic field exerts no force on a bar magnet that is in that magnetic field.
You have probably had some experience with bar magnets. You know that like poles repel and unlike poles attract. And, from your study of the electric field, you have probably (correctly) hypothesized that in the field point of view, the way we see this is that one bar magnet (call it the source magnet) creates a magnetic field in the region of space around itself, and, that if there is another bar magnet in that region of space, it will be affected by the magnetic field it is in. We have already discussed the fact that the victim bar magnet will experience a torque. But you know, from your experience with bar magnets, that it will also experience a force. How can that be when I just stated that a uniform magnetic field exerts no force on a bar magnet? Yes, of course. The magnetic field of the source magnet must be non-uniform. Enough about the nature of the magnetic field of a bar magnet, I’m supposed to save that for an upcoming chapter. Suffice it to say that it is non-uniform and to focus our attention on the effect of a non-uniform field on a bar magnet that finds itself in that magnetic field.
First of all, a non-uniform magnetic field will exert a torque on a magnetic dipole (a bar magnet) just as before (\vec{\tau}=\vec{\mu}\times \vec{B}). But, a non-uniform magnetic field (one for which the magnitude, and/or direction, depends on position) also exerts a force on a magnetic dipole. The force is given by:
\vec{F}_B=\nabla (\vec{\mu}\cdot \vec{B}) \label{15-2}
where
- \vec{F}_B is the force exerted by the magnetic field \vec{B} on a particle having a magnetic dipole moment \vec{\tau}
- \vec{\mu} is the magnetic dipole of the "victim", and,
- \vec{B} is the magnetic field at the position in space where the victim finds itself. To evaluate the force, once must know \vec{B} as a function of x,y and z (wherea \vec{\mu} is a constant) .
Note that after you take the gradient of \vec{\mu}\cdot \vec{B}, you have to evaluate the result at the values of x,y and z corresponding to the location of the victim.
Just to make sure that you know how to use this equation, please note that if \vec{\mu} and \vec{B} are expressed in \hat{i},\hat{j},\hat{k} notation, so that they appear as \vec{\mu}=\mu_x \hat{i}+\mu_y \hat{j}+\mu_z \hat{k} and \vec{B}=B_x \hat{i}+B_y \hat{j}+B_z \hat{k} respectively, then:
\begin{align*} \vec{\mu}\cdot\vec{B} &=(\mu_x \hat{i}+\mu_y \hat{j}+\mu_z \hat{k}) \cdot (B_x \hat{i}+B_y \hat{j}+B_z \hat{k}) \\[4pt] &=\mu_x B_x+\mu_y B_y+\mu_z B_z \end{align*}
And the gradient of \vec{\mu}\cdot\vec{B} (which by equation \ref{15-2} is the force we seek) is given by
\nabla (\vec{\mu}\cdot \vec{B})=\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial x} \hat{i} +\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial y} \hat{j}+\frac{\partial (\vec{\mu}\cdot \vec{B})}{\partial z} \hat{k} \nonumber
where derivatives in this equation can (using \vec{\mu}\cdot\vec{B}=\mu_x B_x+\mu_y B_y+\mu_z B_z from just above) can be expressed as:
\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial x}=\mu_x \frac{\partial B_x}{\partial x}+\mu_y \frac{\partial B_y}{\partial x}+\mu_z \frac{\partial B_z}{\partial x} \nonumber
\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial y}=\mu_x \frac{\partial B_x}{\partial y}+\mu_y \frac{\partial B_y}{\partial y}+\mu_z \frac{\partial B_z}{\partial y} \nonumber
\frac{\partial (\vec{\mu}\cdot\vec{B})}{\partial z}=\mu_x \frac{\partial B_x}{\partial z}+\mu_y \frac{\partial B_y}{\partial z}+\mu_z \frac{\partial B_z}{\partial z} \nonumber
where we have taken advantage of the fact that the components of the magnetic dipole moment of the victim are not functions of position. Also note that the derivatives are all partial derivatives. Partial derivatives are the easy kind in the sense that, when, for instance, you take the derivative with respect to x, you are to treat y and z as if they were constants. Finally, it is important to realize that, after you take the derivatives, you have to plug the values of x,y and z corresponding to the location of the magnetic dipole (the victim), into the given expression for the force.
Example 3
There exists, in a region of space, a magnetic field, given in terms of Cartesian unit vectors by:
\vec{B}=-5.82\times 10^{-6} T\cdot m \frac{y}{x^2+y^2} \hat{i}+5.82\times 10^{-6} T\cdot m \frac{x}{x^2+y^2} \hat{j} \nonumber
A particle is in the region of space where the magnetic field exists. The particle has a magnetic dipole moment given by:
\vec{\mu}=.514A \cdot m^2 \hat{i} \nonumber
The particle is at (0.110m, 0, 0).
Find the force exerted on the particle by the magnetic field.
Solution
First, we sketch the configuration:
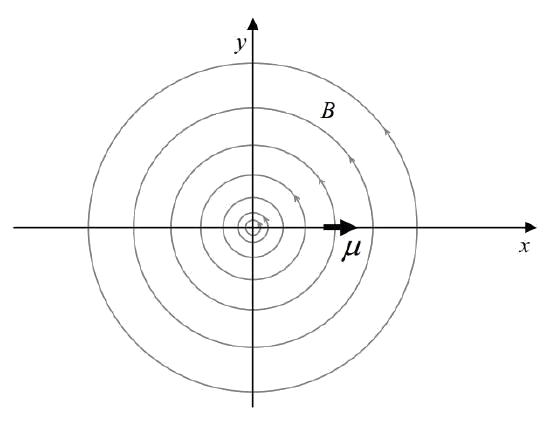
Substituting the given \vec{\mu} and \vec{B}, into our expression for the force yields:
\begin{align*} \vec{F}_B &=\nabla (\vec{\mu}\cdot \vec{B}) \\[4pt] &=\nabla [(0.514A\cdot m^2 \hat{i})\cdot (-5.82\times 10^{-6} T\cdot m \frac{y}{x^2+y^2} \hat{i}+5.82\times 10^{-6} T\cdot m \frac{x}{x^2+y^2} \hat{j})] \\[4pt] &=\nabla \Big( -2.00\times 10^{-6} A\cdot m^2\cdot T\cdot m \frac{y}{x^2+y^2} \Big) \\[4pt] &=-2.99\times 10^{-6} N\cdot m^2 \nabla [y(x^2+y^2)^{-1}] \\[4pt] &=-2.99\times 10^{-6} N\cdot m^2 \Big\{ \frac{\partial}{\partial x}[y(x^2+y^2)^{-1}]\hat{i}+\frac{\partial}{\partial y}[y(x^2+y^2)^{-1}]\hat{j}+\frac{\partial}{\partial z}[y(x^2+y^2)^{-1}]\hat{k} \Big\} \\[4pt] &=-2.99\times 10^{-6} N\cdot m^2 \{[y(-1)(x^2+y^2)^{-2} 2x\hat{i}+[(x^2+y^2)^{-1}+y(-1)(x^2+y^2)^{-2} 2y]\hat{j}+0\hat{k} \\[4pt] &=-2.99\times 10^{-6} N\cdot m^2 \Big\{ -\frac{2xy}{(x^2+y^2)^2} \hat{i} +\Big[ \frac{1}{x^2+y^2}-\frac{2y^2}{(x^2+y^2)^2} \Big] \hat{j} \end{align*}
Recalling that we have to evaluate this expression at the location of the victim, a location that was given as (0.110 m, 0, 0), we find that:
\begin{align*} \vec{F}_B &=-2.99\times 10^{-6} N\cdot m^2 \Big\{-\frac{2(0.110m)0}{[(0.110m^2)+0^2]^2}\hat{i}+\Big[\frac{1}{(0.110m)^2+0^2}-\frac{2(0)^2}{[(0.110m)^2+0^2]^2} \Big] \hat{j} \Big\} \\[4pt] &=-2.47\times 10^{-4} N \hat{j} \end{align*}
Characteristics of the Earth’s Magnetic Field
We live in a magnetic field produced by the earth. Both its magnitude and its direction are different at different locations on the surface of the earth. Furthermore, at any given location, the earth’s magnetic field varies from year to year in both magnitude and direction. Still, on the geographical scale of a college campus, and, on a time scale measured in days, the earth’s magnetic field is approximately uniform and constant.
To align your index finger with the magnetic field of the earth on the Saint Anselm College campus, first point in the horizontal direction 15.4^{\circ} West of North. Then tilt your arm downward so that you are pointing in a direction that is 68.9^{\circ} below the horizontal. (Yes! Can you believe it? It’s mostly downward!) You are now pointing your finger in the direction of the earth’s magnetic field. The magnitude of the magnetic field, on the Saint Anselm College campus, is 5.37\times 10^{-5} T. In other words:
| Characteristic | Value | Rate of Change |
|---|---|---|
| Declination | -15.4^{\circ} | +0.074 ^{\circ}/\mbox{year} |
| Inclination (Dip Angle) | 68.8^{\circ} | -0.096 ^{\circ}/\mbox{year} |
| Magnitude | 5.36\times 10^{-5}T | -0.012\times 10^{-5} T/\mbox{year} |
| Horizontal Component | 1.93\times 10^{-5}T | +0.004\times 10^{-5} T/\mbox{year} |
| Vertical Component | 5.00\times 10^{-5}T | -0.014\times 10^{-5} T/\mbox{year} |
A compass needle is a tiny bar magnet that is constrained to rotate about a vertical axis. The earth’s magnetic field exerts a torque on the compass needle that tends to make the compass needle point in the direction of the horizontal component of the earth’s magnetic field, a direction we call “magnetic north”. Recall that when we talk about which way a bar magnet (such as a compass needle) is pointing, we imagine there to be an arrowhead at its north pole.


