B25: Polarization
( \newcommand{\kernel}{\mathrm{null}\,}\)
The polarization direction of light refers to the two directions or one of the two directions in which the electric field is oscillating. For the case of completely polarized light there are always two directions that could be called the polarization direction. If a single direction is specified, then that direction, and the exact opposite direction, are both the directions of polarization. Still, specifying one direction completely specifies the direction of polarization. For instance for light that is traveling straight downward near the surface of the earth, if the polarization direction is said to be a compass heading of 15∘, that unambiguously means that the electric field oscillates so that it is at times pointing in the direction with a compass heading of 15∘, and at times pointing in the direction with a compass heading of 195∘ (15∘ west of south).
Randomly polarized light, a.k.a. unpolarized light, has electric field oscillations in each and every direction perpendicular to the direction in which the light is traveling. Such light is often depicted, as viewed from behind, (where forward is the direction in which the light is traveling) as:
Vertically polarized light traveling horizontally away from you is typically depicted as:
where the direction in which the light is traveling is “into the page” and upward is “toward the top of the page.” At a particular position through which the light is traveling, starting at an instant when the electric field vector at that position is upward and maximum, the electric field will decrease to zero, then be downward and increasing, reach a maximum downward, then be downward and decreasing, become zero, then be upward and increasing, then reach a maximum upward, and repeat, continually. The diagram depicting the polarization indicates the directions that the electric field does point, at some time during its oscillations. It in no way is meant to imply that the electric field is pointing in two directions at the same time.
Light that is traveling horizontally away from you that is polarized at 30∘ with respect to the vertical could be either:
or
If you encounter such an ambiguous specification of polarization in a problem statement then the answer is the same for either case, so, it doesn’t matter which of the two possible polarization directions you pick. Pick one arbitrarily and work with it.
Light that is traveling horizontally away from you and is polarized, from your point of view, at 30∘ clockwise from the vertical is, however, unambiguously:
Polarizers
A plastic material is manufactured in the form of flat sheets that polarize light that travels through them. A sample of such a flat sheet is called a polarizer. In use, one typically causes light to travel toward a polarizer along a direction that is perpendicular to the polarizer. In other words, one causes the light to be normally incident upon the polarizer.
Schematically, one typically depicts a polarizer by means of a rectangle or a circle filled with parallel line segments.
The orientation of the lines is referred to as the polarization direction of the polarizer. The effect of a polarizer is to transmit light that is polarized in the same direction as that of the polarizer, and to block (absorb or reflect) light that is polarized at right angles to the direction of the polarizer.
The polarization direction of the rectangular polarizer depicted above is vertical. So, it lets vertically-polarized light through and blocks horizontally-polarized light.
The polarization direction of the circle-shaped sample of polarizing material depicted above is horizontal. So, it lets horizontally-polarized light through and blocks vertically-polarized light.
When unpolarized light (a.k.a. randomly-polarized light) is normally incident on any polarizer, half the light gets through. So, if the intensity of the incoming light is I0, then the intensity of the light that gets through, call it I1, is given by:
I1=12I0
In completely unpolarized light, the electric field vectors are oscillating in every direction that is perpendicular to the direction in which the light is traveling. But all the electric field vectors are, as the name implies, vectors. As such, we can break every single one of them up into a component along the direction of polarization of the polarizer and a component that is perpendicular to the polarization direction of the polarizer. A polarizer will let every component that is along the direction of polarization of the polarizer through, and block every component that is perpendicular to the polarization direction. In completely unpolarized light, no matter what the direction of polarization of the polarizer is, if you break up all the electric field vectors into components parallel to and perpendicular to the polarizer’s polarization direction, and add all the parallel components together, and then separately add all the perpendicular components together, the two results will have the same magnitude. This means that we can view completely unpolarized light as being made up of two halves: half polarized parallel to the polarizer’s polarization direction, and half polarized perpendicular to the polarizer’s polarization direction. The half that is polarized parallel to the polarizer’s polarization direction gets through the polarizer, and the other half doesn’t.
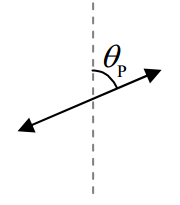
Unpolarized Light Traveling Directly Away From You
| When completely unpolarized light of intensity I0... | ... is normally incident on a polarizer whose polarization direction makes an angle θp with the vertical... | ... the light that gets through is polarized in the polarizer's direction of polarization, and, has an intensity I1=12I0. |
Note how the effect of a polarizer on the intensity of normally-incident unpolarized light does not depend on the orientation of the polarizer. You get the same intensity I1=12I0 of light getting through the polarizer, no matter what the direction of polarization of the polarizer is.
Now suppose that we have some light that, for whatever reason, is already polarized. When polarized light is normally incident on a polarizer, the intensity of the light that gets through does depend on the direction of polarization of the polarizer (relative to that of the incoming light). Suppose for instance, that the incoming light,
is polarized at an angle θ with respect to the polarization direction of a polarizer upon which the light is normally incident:
Before it hits the polarizer, the light’s electric-field-oscillations-amplitude vector,
can be broken up into a component parallel to the polarizer’s polarization direction and a component perpendicular to the polarizer’s polarization direction.
The parallel component E∥ = E cos \theta\) gets through the polarizer, the perpendicular component does not.
Now the intensity of polarized light is proportional to the square of the amplitude of the oscillations of the electric field. So, we can express the intensity of the incoming light as
Io=(constant)E2
and the intensity of the light that gets through as:
I1=(constant)E2∥
I1=(constant)(Ecosθ)2
I1=(constant)E2(cosθ)2
I1=Io(cosθ)2
Summarizing:
Polarized Light Traveling Directly Away From You
| When polarized light of intensity I0... | ... is normally incident on a polarizer whose polarization direction makes an angle θ with the polarization direction of the light... |
... the light that gets through is polarized in the polarizer's direction of polarization, and, has an intensity I1=I0(cosθ)2. |