11.3: Some Consequences of the Lorentz Transformations

LOSS OF SIMULTANEITY

If two events are simultaneous for a moving observer in $S^\prime$, the observer measures their time interval as $\Delta t^\prime$. If the two events happen at the same position ($\Delta x^\prime = 0$), the Lorentz transformations give $\Delta x=0, \Delta t=0$ as well. However, if the two events in $S^\prime$ are spatially separate ($\Delta x \neq 0$), we find that for an observer in $S$ $\Delta t = \gamma (u)(u/c^2)\Delta x^\prime$, and therefore the two events are not simultaneous. Things even get worse: suppose two events A and B happen in $S$ a distance $\Delta x$ apart, and a time interval $\Delta t$ after each other. Now if $\Delta x > (c/u)c\Delta t$, a moving observer in $S^\prime$ will conclude that $\Delta t ^\prime <0$, which means that event B happens before event A! Fortunately, this does not violate causality, as a signal from A to B (or vice versa) will at most travel with the speed of light, which, as we will see in the next section, means that for the conditions given, A and B cannot be causally connected - i.e., you cannot reverse cause and effect, no matter how fast you run.

TIME DILATION AND LORENTZ CONTRACTION

A stationary observer in frame $S^\prime$ measures the time difference between two points to be $\Delta t^\prime$ on his/her own clock, while an observer in $S$ will measure the time difference on that (moving) clock to be $\Delta t = \gamma (u)\Delta t^\prime$, exactly the time dilation result we found in equation (10.2.1). Likewise, an observer in $S^\prime$ will measure the length of a stationary stick to be $\Delta L^\prime$. For an observer in $S$, using a method that reaches the ends of the stick simultaneously (so $\Delta t = 0$), the length is $\Delta L$. We have $\Delta x^\prime = \Delta L^\prime = \gamma(u)\Delta L$, so $\Delta L=\Delta L^\prime/\gamma(u)$, which (unsurprisingly) is the Lorentz contraction result of equation (10.2.5).

VELOCITY ADDITION

We calculated the speed of an object $v$ as measured in $S$ as a function of the speed $v^\prime$ in $S^\prime$ and the speed $u$ of $S^\prime$ in equation (11.2.5). Substituting the values of the constants we found later, we get the following equation:

$$v=\frac{u+v^{\prime}}{1+u v^{\prime} / c^{2}}\label{eq:1}$$

Equation ($\ref{eq:1}$) thus follows directly from the light postulate - that is all we used to derive it. It mathematically shows you can never add velocities in such a way as to exceed the speed of light. Setting $u=v^\prime=c$ gives $v=c$, and for any values $u<c$, $v^\prime<c$, you’ll always get $v<c$.

Equation $\ref{eq:1}$ holds for motion in the same direction as the motion of the reference frame - for example, if you’re on a moving train, and rolling a ball down the length of the train. However, you could also roll the ball in the transverse direction (say $y$ if we call the direction in which the train is moving $x$). You might think that the observed velocity for the comoving and stationary observer is the same in that case (it is for Galilean transformations), but that’s not the case. We have $v_y = dy/dt$, and although $dy$ is invariant, $dt$ is not. Calculating $v_y$ in terms of $v_y^\prime$ (the speed at which the moving observer rolls the ball) is straightforward though, we simply apply the Lorentz transformation to $dt$:

$$v_{y}=\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{\mathrm{d} y^{\prime}}{\gamma(u) \mathrm{d}\left(t^{\prime}+\frac{u}{c^{2}} x^{\prime}\right)}=\frac{1}{\gamma(u)} \frac{\mathrm{d} y^{\prime} / \mathrm{d} t^{\prime}}{1+\frac{u}{c^{2}} \mathrm{d} x^{\prime} / \mathrm{d} t^{\prime}}=\frac{1}{\gamma(u)} \frac{v_{y}^{\prime}}{1+u v_{x}^{\prime} / c^{2}}\label{eq:2}$$

EXAMPLE APPLICATION: RELATIVISTIC HEADLIGHT EFFECT

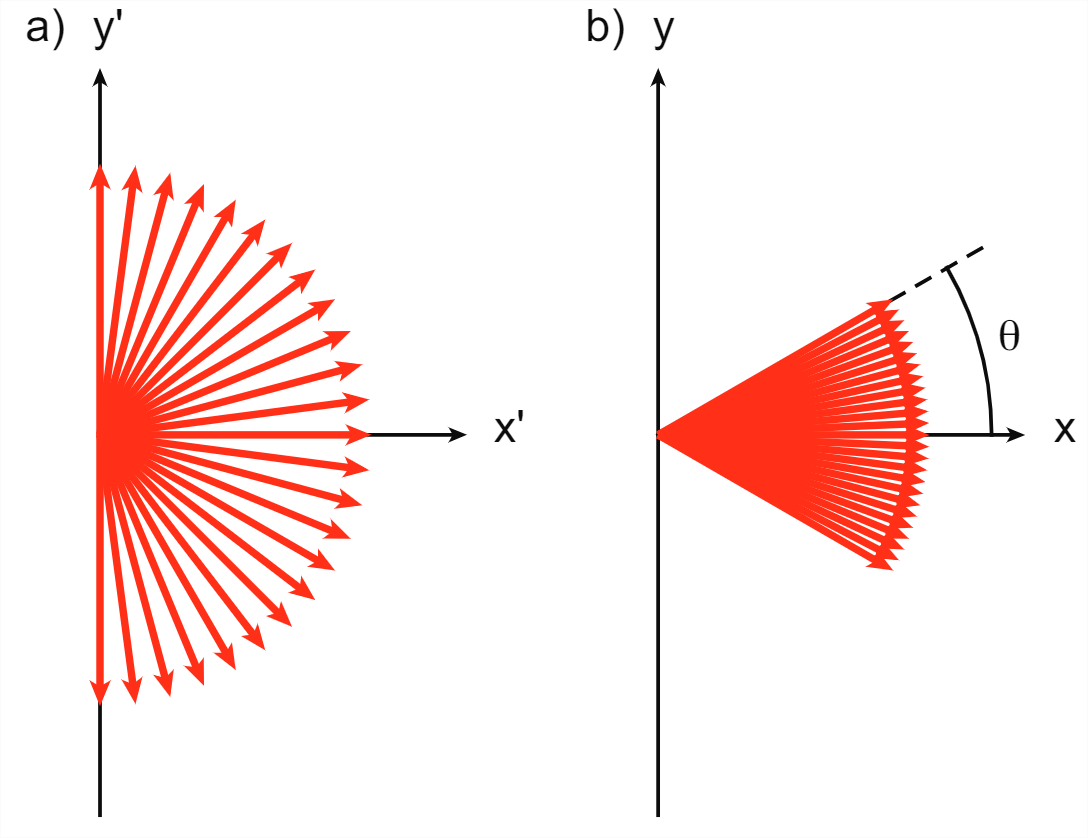
Suppose you have a light source that radiates isotropically (i.e., with the same intensity in all directions). What happens if we put the light source on a moving train? Remarkably, according to a stationary observer, the light source is not isotropic anymore. To understand what happens, let us as usual call the direction in which the train moves $x$ and its speed $u$. A ray of light emitted by the light source in $S^\prime$ has a velocity $v^\prime$ with magnitude $c$ (on which both observers agree), and components ($v_x^\prime$, $v_y^\prime$, $v_z^\prime$) (figure $\PageIndex{1}$a). Now let’s consider the ray of light that moves along the $y^\prime$ axis. Its velocity is given by $v^\prime = (0,c,0$\). We can calculate the velocity components of this ray of light in frame $S$ using the velocity transformation Equations $\ref{eq:1}$ and $\ref{eq:2}$, which gives $v=(u,\gamma(u),0)$ (which of course still has magnitude $c$). The ray of light thus picks up a component in the positive $x$ direction, and consequently gets a smaller component in the $y$ direction. Figure $\PageIndex{1}$b shows the resulting light cone in the positive $x$ direction. Its opening angle $\mu$ can be easily calculated:

$$\sin (\theta)=\frac{v_{y}}{|v|}=\frac{v_{y}}{c}=\gamma(u)$$

For reasons that you will probably find easy to guess, this phenomenon is known as the relativistic headlight effect. It is observed in the radiation emitted by electrons rotating around magnetic field lines orbiting Jupiter and the sun, as well as in particle accelerators on earth.

Figure $\PageIndex{1}$: Relativistic headlight effect. (a) Isotropic light source in the comoving frame $S^\prime$. (b) The same light source as observed from a stationary frame $S$. The opening angle $\mu$ is given by $\sin(\mu)=\gamma(\mu)$.