10.E: Einstein's Postulates (Exercises)
- Page ID
- 17426
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)10.1
Suppose you wake up in Rotterdam (10 km from Delft) 1 minute before class in Delft starts (i.e., at 8:44). You dress quickly, but have only 10 seconds left to get to Delft. You happen to be a very fast biker, making it exactly when your watch shows 8:45. Will the rest of the class agree that you arrived just in the nick of time?
10.2
A well-known (but probably apocryphal) Einstein quote is ‘Sit on a hot stove for five minutes, and it feels like an hour. Talk to a pretty girl for an hour, and it feels like five minutes. That’s relativity.’
(a) Einstein (at rest, frame \(S\)) sits on pins and needles for five minutes. Could there be a moving frame \(S_0\) in which this same period lasts an hour? If so, determine the velocity of that frame with respect to \(S\), if not, explain why not.
(b) Einstein talks with Marilyn Monroe for an hour. (According to another well-known anecdote, during this conversation Marilyn Monroe would have said to Einstein ‘If we were to have children, and they’d have your brains and my looks, wouldn’t that be fantastic?’, to which Einstein replied ‘Yes, but what if they’d have your brains and my looks?’). Both Einstein and Monroe are at rest in frame \(S\). Could there be a moving frame \(S_0\) in which this same period lasts five minutes? If so, determine the velocity of that frame with respect to S, if not, explain why not.
10.3
How fast would you have to fly such that you cover exactly one lightyear (as measured by a stationary observer) in one year (as measured on your clock)?
10.4
Adding velocities Einstein postulated that the speed of light (in vacuum, but we’ll ignore that point) is the same in any inertial reference frame. Consequently, for any object with mass, the speed of light is also the absolute limit: you can never reach it, let alone exceed it. That doesn’t fit well with everyday experience: if you’re on a train moving at speed \(u\), and throw a ball at speed \(v\), an outside (stationary) observer will measure the ball’s speed to be \(u + v\). There seems to be no fundamental reason why we couldn’t take, say, \(u=v=0.8c\), which would imply that the outside observer measures the ball to go at \(1.6c\). The strange thing is that (s)he doesn’t - the outside observer will tell you that they measured a speed of only \(0.976c\). The reason is that although both you and the outside observer consider speed to be the distance traveled divided by the time it took to travel that distance, you no longer measure either the same distance or the same time at such high speeds. In this exercise, we’ll derive a new equation for adding speeds, which shows that you can never break the speed-of-light limit.
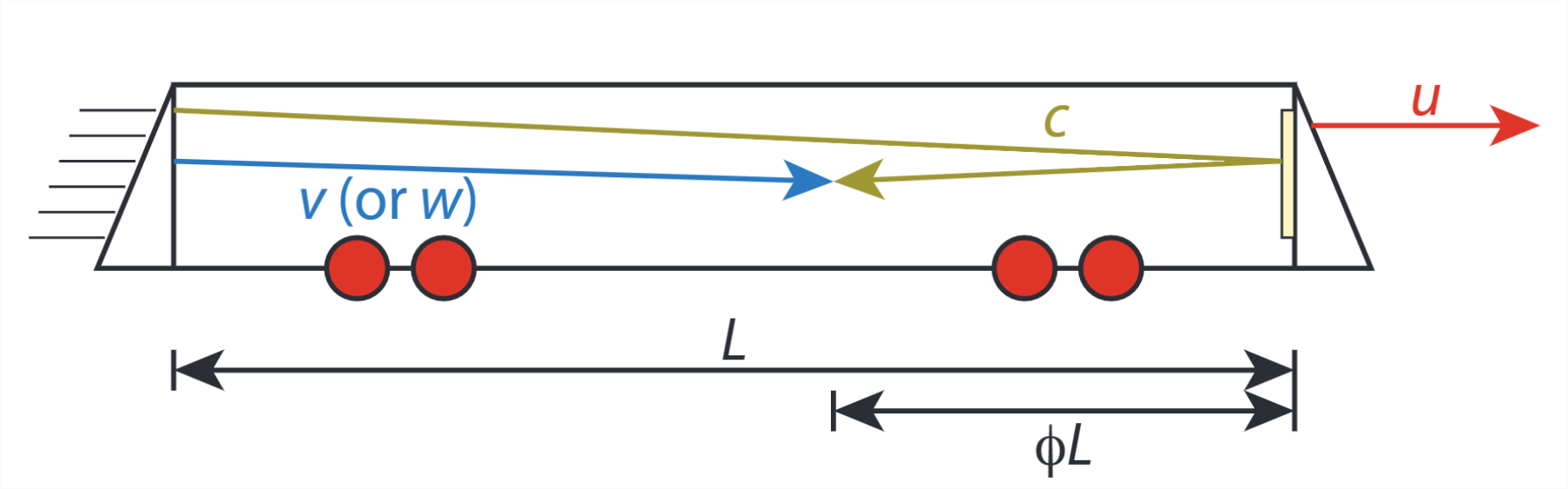
We consider the situation sketched in figure \(\PageIndex{1}\). A train is moving with speed \(u\). Someone standing at the back of the train car fires a photon (yellow, speed \(c\)) and a bullet (blue) at the same time. As measured on the train, the bullet has speed \(v\); for an outside observer, the bullet has speed \(w\). The photon is reflected by a mirror at the front of the car, and meets up with the bullet at a point a distance \(\phi L\) from the front. Note that \(L\), the length of the car, is measured differently by the comoving and stationary (outside) observer, as is the time interval between firing and meeting of the photon and bullet. However, both observers agree that at the events of firing and meeting the photon and bullet are at the same place in space and time. We’ll use these two points to find a relation between the speeds of the bullet as observed in the stationary and comoving frame, and the speed of the train.
(a) First, you’ll take the point of view (and spacetime coordinates) of the outside observer. Denote the length of the train (as observed by you) by \(L\), the time it takes the photon to reach the front of the train by \(t_1\), and the time it takes to return to the meeting point by \(t_2\). The train moves at speed \(u\), the observed velocity of the bullet is \(w\) and that of the photon is (obviously) \(c\). Express \(ct_1\), the distance traveled by the photon in \(t_1\), in terms of \(L\), \(u\), and \(t_1\).
(b) Now express \(ct_2\), the distance traveled by the photon in \(t_2\), in terms of \(L\), \(u\), \(t_2\), and \(\phi\).
(c) From the two equations you have, eliminate \(L\) and then rewrite the resulting equation in an expression for \(t_2/t_1\).
(d) Argue that \(w\left(t_{1}+t_{2}\right)=c\left(t_{1}-t_{2}\right)\) by considering where the bullet and photon meet up.
(e) Rewrite the expression in (4d) to also give an expression for \(t_2/t_1\).
(f ) Equate the expressions you found in (4c) and (4e), then rewrite them as an expression for \(\phi\).
(g) Now we’ll take the comoving point of view. Find another expression for \(\phi\). Hint: you can either repeat the procedure above for the comoving observer, or ‘translate’ the expression in (4f) directly to the comoving frame.
(h) Equate the two expressions for \(\phi\) to get an expression for \(w\) that only contains \(u\), \(v\) and \(c\).
(i) The rest is algebra: show that the expression you found in (4h) can be rewritten as: \[w=\frac{v+u}{1+u v / c^{2}}\].
10.5
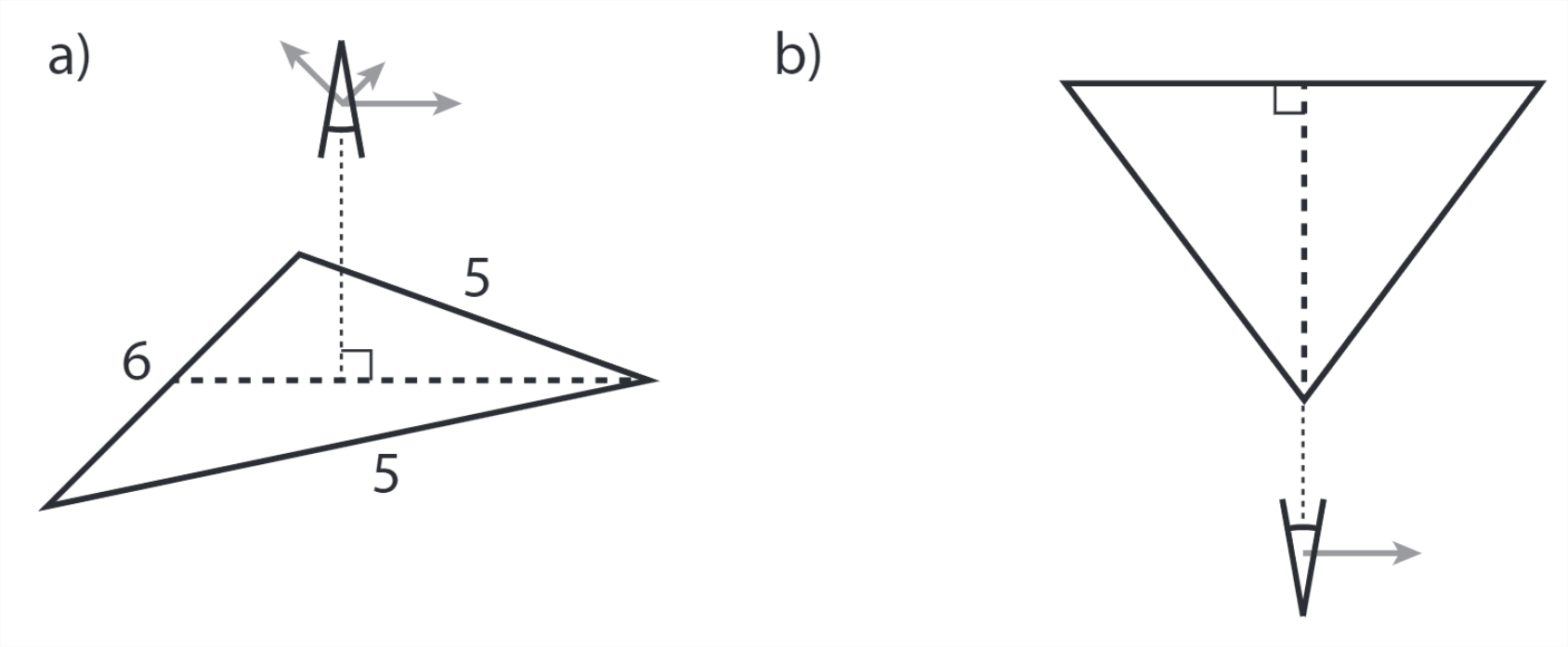
[Challenging] Three bars are welded together into the shape of an isosceles triangle with side ratios 5:5:6. An observer looks at our triangle from a direction perpendicular to the plane it spans, as in figure a. The observer moves with relativistic velocity \(v\) in a direction parallel to the plane of the triangle.
(a) In which direction and at which speed should the observer be moving so that according to him, the triangle is equilateral?
(b) We now rotate the triangle in such a way that all its corners and the observer are in one plane. The longest side of the triangle is arranged perpendicular to the observer’s line of sight, and at the far end, as in figure b. The observer moves with speed \(v\) (not necessarily the same speed as in part (a) in the direction parallel to this long edge. Show that the observer sees a distorted triangle.
(c) As the observer keeps moving along the same line as in (b), show that it seems to him as if the triangle is rotating, and determine in which direction it rotates.