Doppler shift
- Page ID
- 1916
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
It is simplest to think of Doppler shift for sound waves. Everyone is familiar with the sound of a passing car. When it is approaching you the pitch is high, and it gets lower as it passes you and recedes into the distance. The explanation is that the sound waves have a fixed wavelength (distance between two crests or two troughs) only if you're not moving relative to the source of the sound. If you are moving away from the source (or equivalently it is receding from you) then each crest will take a little longer to reach you, and so you'll perceive a longer wavelength. Similarly if you're approaching the source, then you'll be meeting each crest a little earlier, and so you'll perceive a shorter wavelength.
Since long wavelength's (low frequencies) mean lower notes and shorter wavelengths (higher frequencies) mean higher notes, then you hear a higher pitch if you and the source are approaching each other and a lower pitch if you're moving apart.
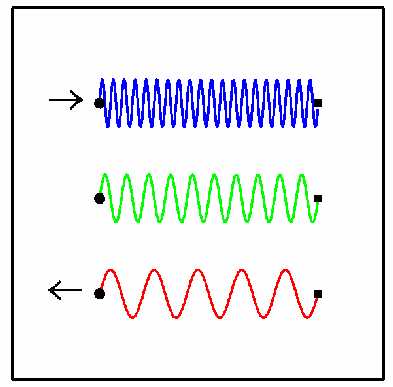
The same principle applies for light as well as for sound. In detail the amount of shift depends a little differently on the speed, since we have to do the calculation in the context of special relativity. But in general it's just the same: if you're approaching a light source you see shorter wavelengths (a blue-shift), while if you're moving away you see longer wavelengths (a red-shift).
The main difference between light and sound is that to get a detectable Doppler effect you have to be moving at a speed which isn't tiny relative to the speed of the waves. That's about 300 meters per second for sound, but 300 million meters per second for light! So it's easy to hear the change in pitch when a car whizzes past you, but it's very hard to detect the change in color of the car! On the other hand, a very sensitive device could measure this change, which is just what happens when a speeding motorist is caught in a radar speed trap.
Distant galaxies are moving away from us extremely fast. So fast in fact that it is relatively easy to measure the shift in their spectral lines. This is evidence that the Universe is expanding, which is one of the most important pieces of evidence in support of the Big Bang picture.
Contributors and Attributions
Martin White (Physics, University of California, Berkeley)

