3.3: Plane Waves

As we have just seen, a wave of amplitude \(\begin{equation}A\end{equation}\), wavenumber \(\begin{equation}k\end{equation}\), angular frequency \(\begin{equation}\omega\end{equation}\), and phase angle \(\begin{equation}\varphi\end{equation}\), propagating in the positive \(\begin{equation}x\end{equation}\)-direction, is represented by the following wavefunction:

\begin{equation}\psi(x, t)=A \cos (k x-\omega t+\varphi)\end{equation}

Now, the type of wave represented above is conventionally termed a one-dimensional plane wave. It is one-dimensional because its associated wavefunction only depends on the single Cartesian coordinate \(\begin{equation}x\end{equation}\). Furthermore, it is a plane wave because the wave maxima, which are located at

\begin{equation}k x-\omega t+\varphi=j 2 \pi\end{equation}

where \(\begin{equation}j\end{equation}\) is an integer, consist of a series of parallel planes, normal to the \(\begin{equation}x\end{equation}\)-axis, which are equally spaced a distance \(\begin{equation}\lambda=2 \pi / k\end{equation}\) apart, and propagate along the positive -axis at the velocity \(\begin{equation}v=\omega / k\end{equation}\). These conclusions follow because Eq. (3.3.2) can be re-written in the form

\begin{equation}x=d\end{equation}

where \(\begin{equation}d=(j-\varphi / 2 \pi) \lambda+v t\end{equation}\). Moreover, as is well-known, (3.2.3) is the equation of a plane, normal to the -axis, whose distance of closest approach to the origin is .

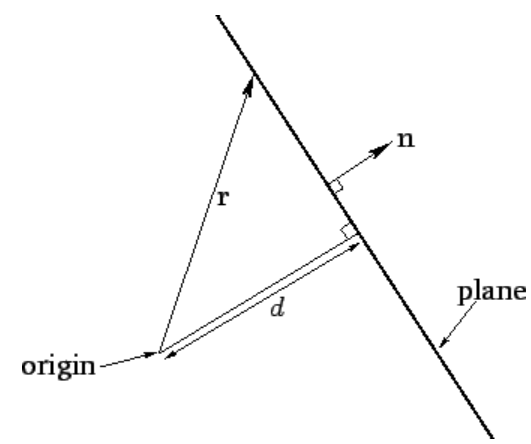
Figure 1: The solution of  \(\begin{equation}\mathbf{n} \cdot \mathbf{r}=d\end{equation}\) is a plane.

The previous equation can also be written in the coordinate-free form

\begin{equation}\mathbf{n} \cdot \mathbf{r}=d\end{equation}

where \(\begin{equation}\mathbf{n}=(1,0,0)\end{equation}\)  is a unit vector directed along the positive -axis, and \(\begin{equation}\mathbf{r}=(x, y, z)\end{equation}\) represents the vector displacement of a general point from the origin. Since there is nothing special about the -direction, it follows that if  is re-interpreted as a unit vector pointing in an arbitrary direction then (3.3.4) can be re-interpreted as the general equation of a plane. As before, the plane is normal to , and its distance of closest approach to the origin is . See Fig. 1. This observation allows us to write the three-dimensional equivalent to the wavefunction (3.3.1) as 

\begin{equation}\psi(x, y, z, t)=A \cos (\mathbf{k} \cdot \mathbf{r}-\omega t+\varphi)\end{equation}

where the constant vector \(\begin{equation}\mathbf{k}=\left(k_{x}, k_{y}, k_{z}\right)=k \mathbf{n}\end{equation}\) is called the wavevector. The wave represented above is conventionally termed a three-dimensional plane wave. It is three-dimensional because its wavefunction, \(\begin{equation}\psi(x, y, z, t)\end{equation}\), depends on all three Cartesian coordinates. Moreover, it is a plane wave because the wave maxima are located at 

\begin{equation}\mathbf{k} \cdot \mathbf{r}-\omega t+\varphi=j 2 \pi\end{equation}

or

\begin{equation}\mathbf{n} \cdot \mathbf{r}=(j-\varphi / 2 \pi) \lambda+v t\end{equation}

where \(\begin{equation}\lambda=2 \pi / k, \text { and } v=\omega / k\end{equation}\). Note that the wavenumber, \(\begin{equation}k\end{equation}\), is the magnitude of the wavevector, \(\begin{equation}\mathbf{k}: \text { i.e.}, k \equiv|\mathbf{k}|\end{equation}\). It follows, by comparison with Eq. (3.3.4), that the wave maxima consist of a series of parallel planes, normal to the wavevector, which are equally spaced a distance \(\begin{equation}\lambda\end{equation}\) apart, and which propagate in the \(\begin{equation}\mathbf{k}\end{equation}\)-direction at the velocity . See Fig. 2. Hence, the direction of the wavevector specifies the wave propagation direction, whereas its magnitude determines the wavenumber, , and, thus, the wavelength, \(\begin{equation}\lambda=2 \pi / k\end{equation}\)

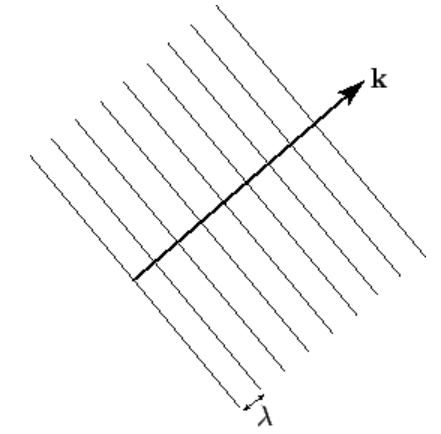
Figure 2: Wave maxima associated with a three-dimensional plane wave.

Contributors

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)