Skip to main content
\(\require{cancel}\)
Physics LibreTexts

4.5: Motion in Central Field

  1. Last updated
    08:26, 16 Nov 2014
  2. Save as PDF

Consider a particle of mass \(M\) moving in a spherically symmetric potential. The Hamiltonian takes the form

\[H = \frac{{p}^2}{2\,M} + V(r). \tag{387}\]

Adopting Schrödinger's representation, we can write 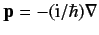$ {\bf p} = -({\rm i}/\hbar) \nabla$ . Hence,

 

$\displaystyle H = -\frac{\hbar^2}{2\,M}\, \nabla^2 + V(r).$ (388)

 

 

When written in spherical polar coordinates, the above equation becomes

 

$\displaystyle H= -\frac{\hbar^2}{2\,M}\left[ \frac{1}{r^2}\frac{\partial}{\part... ...+ \frac{1}{r^2\sin^2\theta} \frac{\partial^2}{\partial\varphi^2}\right] + V(r).$ (389)

 

 

Comparing this equation with Equation (374), we find that

 

$\displaystyle H= \frac{\hbar^2}{2\,M}\left(- \frac{1}{r^2}\frac{\partial}{\partial r} \,r^2\,\frac{\partial}{\partial r} + \frac{L^2}{\hbar^2 r^2}\right) + V(r).$ (390)

 

 

Now, we know that the three components of angular momentum commute with $ L^2$ (see Section 4.1). We also know, from Equations (369)-(371), that $ L_x$ , $ L_y$ , and $ L_z$ take the form of partial derivative operators involving only angular coordinates, when written in terms of spherical polar coordinates using the Schrödinger representation. It follows from Equation (390) that all three components of the angular momentum commute with the Hamiltonian:

 

$\displaystyle [{\bf L}, H] = 0.$ (391)

 

 

It is also easily seen that $ L^2$ (which can be expressed as a purely angular differential operator) commutes with the Hamiltonian:

 

$\displaystyle [L^2, H] = 0.$ (392)

 

 

According to Section 3.2, the previous two equations ensure that the angular momentum $ {\bf L}$ and its magnitude squared $ L^2$ are both constants of the motion. This is as expected for a spherically symmetric potential.

Consider the energy eigenvalue problem

 

$\displaystyle H\,\psi = E\,\psi,$ (393)

 

 

where $ E$ is a number. Since $ L^2$ and $ L_z$ commute with each other and the Hamiltonian, it is always possible to represent the state of the system in terms of the simultaneous eigenstates of $ L^2$ , $ L_z$ , and $ H$ . But, we already know that the most general form for the wavefunction of a simultaneous eigenstate of $ L^2$ and $ L_z$ is (see previous section)

 

$\displaystyle \psi(r, \theta, \varphi) = R(r) \,Y_{l\,m}(\theta, \varphi).$ (394)

 

 

Substituting Equation (394) into Equation (390), and making use of Equation (382), we obtain

 

$\displaystyle \left[\frac{\hbar^2}{2\,M} \left(-\frac{1}{r^2} \frac{d}{dr}\,r^2\,\frac{d}{dr} +\frac{l\,(l+1)}{r^2}\right) + V(r) - E\right] R = 0.$ (395)

 

 

This is a Sturm-Liouville equation for the function $ R(r)$ . We know, from the general properties of this type of equation, that if $ R(r)$ is required to be well-behaved at $ r=0$ and as $ r\rightarrow \infty$ then solutions only exist for a discrete set of values of $ E$ . These are the energy eigenvalues. In general, the energy eigenvalues depend on the quantum number $ l$ , but are independent of the quantum number $ m$ .

Contributors